Download document 8901545

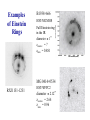
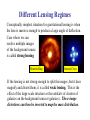
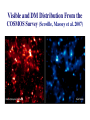
Ay 127
ISM, Cosmic Web, and
Gravitational Lensing
Intergalactic Medium (IGM)
•  Essentially, baryons between galaxies
•  Its density evolution follows the LSS formation, and the potential
wells defined by the DM, forming a web of filaments, the cocalled “Cosmic Web”
•  An important distinction is that this gas unaffiliated with galaxies
samples the low-density regions, which are still in a linear regime
•  Gas falls into galaxies, where it serves as a replenishment fuel for
star formation
•  Likewise, enriched gas is driven from galaxies through the
radiatively and SN powered galactic winds, which chemically
enriches the IGM
•  Chemical evolution of galaxies and IGM thus track each other
•  Star formation and AGN provide ionizing flux for the IGM
Cosmic Web: Numerical Simulations
Our lines of sight towards some luminous background sources
intersect a range of gas densities, condensed clouds, galaxies …
(from R. Cen)
QSO Absorption Line Systems
•  An alternative to searching for galaxies by their emission
properties is to search for them by their absorption
•  Quasars are very luminous objects and have very blue colours
which make them relatively easy to detect at high redshifts
•  Nowadays, GRB afterglows provide a useful alternative
•  Note that this has
different selection
effects than the
traditional imaging
surveys: not by
luminosity or surface
brightness, but by the
cross section (size) and
column density
Types of QSO Absorption Lines
•  Lyman alpha forest:
–  Numerous, weak lines from low-density hydrogen clouds
–  Lyman alpha clouds are proto-galactic clouds, with low density,
they are not galaxies (but some may be proto-dwarfs)
•  Lyman Limit Systems (LLS) and “Damped” Lyman alpha (DLA)
absorption lines:
–  Rare, strong hydrogen absorption, high column densities
–  Coming from intervening galaxies
–  An intervening galaxies often produce both metal and damped
Lyman alpha absorptions
•  Helium equivalents are seen in the far UV part of the spectrum
•  “Metal” absorption lines
–  Absorption lines from heavy elements, e.g., C, Si, Mg, Al, Fe
–  Most are from intervening galaxies
Types of QSO
Absorption
Systems
Measuring the Absorbers
We measure equivalent widths of the
lines, and in some cases shapes of the
line profiles
They are connected to the column
densities via curves of growth 
The shape of the line
profile is also a function of
the pressure, which causes
a Doppler broadening, and
also the global kinematics
of the absorbing cloud
Absorber Cross Sections
Column density of
neutral H is higher at
smaller radii, so LLS
and DLA absorbers
are rare
Metals are ejected
out to galactic
coronae, and their
column densities and
ionization states
depend on the radius
Ly α Absorbers
•  Ly α Forest: 1014 ≤ NHI ≤ 1016 cm-2
–  Lines are unsaturated
–  Primordial metalicity < solar
–  Sizes are > galaxies
•  Ly Limit Systems (LLS): NHI ≥ 1017 cm-2
–  Ly α Lines are saturated
–  NHI is ufficient to absorb all ionising photons shortward of the Ly
limit at 912Å in the restframe (i.e., like the UV-drop out or
Lyman-break galaxies)
•  Damped Ly α (DLA) Systems: NHI ≥ 1020 cm-2
–  Line heavily saturated
–  Profile dominated by “damped” Lorentzian wings
–  Almost surely proto-disks or their building blocks
Fitting the
Forest:
A Damped Lyman α System
Distribution of Column Densities
f (NHI) ~ NHI-1.7
Ly α Forest
LLS
DLA
Evolution of the Hydrogen Absorbers
Low redshift QSO
High redshift QSO
Evolution of Ly α Absorbers
(from Rauch 1998, ARAA, 36, 267)
(NB: this is for Λ = 0 cosmology!)
Typical γ ~ 1.8 (at high z’s)
Evolution of Ly α Absorbers
The numbers are higher at higher z’s, but it is not yet clear how much
of the effect is due to the number density evolution, and how much to
a possible cross section evoluton - nor why is there a break at z ~ 1.5
The Forest Thickens
Estimating the Evolution of Gas Density
(from Wolfe et al. 2005, ARAA, 43, 861)
Evolution of Neutral Gas
The Gunn-Peterson Effect
Even a slight amount of neutral hydrogen in the early IGM
can completely absorb the flux blueward of Lyα
(from Fan et al. 2006, ARAA, 44, 415)
“Gunn-Peterson like” troughs are now observed
along all available lines-of-sight at at z ~ 6
Lyβ
G-P
ò
G-P
Transmitted Lyα Flux vs. Redshift
(from Fan et al. 2006, ARAA, 44, 415)
The Absorber - Galaxy Connection
•  Metallic line absorbers are generally believed to be associated
with galaxies (after all, stars must have made the metals)
An example with multiple metallic line systems:
Galaxy Counterparts of DLA Systems
•  Several examples are known with
Lyα line emission
•  Properties (size, luminosity,
SFR) are typical of field galaxies
at such redshifts, and consistent
with being progenitors of z ~ 0
disks
Numerical Simulations of IGM
DLA systems as the
densest knots in the
cosmic web
However, the
simulations cannot
resolve whether these
are rotating
(proto)disks
(from Katz et al. 1996)
Clustering of Metallic Absorbers
Metallic absorbers
Metallic absorbers
are found to cluster
in redshift space,
even at high z’s,
while Ly α clouds
do not. This further
strengthens their
association with
galaxies
Ly α clouds
Number Density Evolution of Absorbers
While the H I seems
to decline in time
(being burned out in
stars?), the density of
metals seems to be
increasing, as one
may expect
Abundances in DLA Systems and Disks
Solar g
Chemical
Enrichment
Evolution of
DLA Systems
(Wolfe et al.)
But different types
of systems may be
evolving in
different ways …
(from M. Pettini)
IGM Summary
•  Intergalactic medium (IGM) is the gas associated with the large
scale structure, rather than galaxies themselves; e.g., along the
still collapsing filaments, thus the “cosmic web”
–  However, large column density hydrogen systems, and strong
metallic absorbers are always associated with galaxies
•  It is condensed into clouds, the smallest of which form the “Ly α
forest”
•  It is ionized by the UV radiation from star forming galaxies and
quasars
•  It is metal-enriched by the galactic winds, which expel the gas
already processed through stars; thus, it tracks the chemical
evolution of galaxies
•  Studied through absorption spectra against background
continuum sources, e.g., quasars or GRB afterglows
Gravitational Lensing:
Mapping the Distribution of the Dark Matter
•  We know from general relativity that mass - whether it is
visible or not - bends light. This opens a possibility of “seeing”
the distribution of dark matter
•  Chowlson (1924) and Einstein (1936) predicted that if a
background object is directly aligned with a point source mass,
the light rays will be deflected into an “Einstein Ring”
The first gravitational lens
Walsh, Carswell & Weymann 1979
Gravitational
lensing in the
strong regime
Misalignment of
the line of sight
and the center
of the lensing
mass splits the
Einstein ring
into multiple
images
Examples
of Einstein
Rings
B1938+666
HST-NICMOS
Full Einstein ring
in the IR
diameter ≅ 1”
zsource = ?
zlens = 0.881
MG 0414+0534
RXJ1131-1231
HST-WFPC2
diameter ≅ 2.12”
zsource = 2.64
zlens = 0.96
Gravitationally Lensed Galaxies - “Arcs”
In 1937, Zwicky predicted that one could study the mass distribution
(dark matter) in clusters by studying background galaxies that are
lensed by the dark matter in the cluster. This was not observationally
feasible until the mid-1990’s
Gravitational Lensing
Photons are deflected by gravitational fields - hence images of
background objects are distorted if there is a massive foreground
object along the line of sight.
Bending of light is similar to deflection of massive particles, except
that GR predicts that for photons the bending is exactly twice the
Newtonian value:
4GM 2R
α=
bc
2
=
s
b
…where Rs is the Schwarzschild radius of a body of mass M, and
b is the impact parameter. This formula is valid if b >> Rs:
•  Not valid very close to a black hole or neutron star
€ else
•  Valid everywhere
•  Implies that deflection angle a will be small
e.g., for the stars near the Solar limb, ~ 2 arcsec
Geometry for Gravitational Lensing
Consider sources at distance dS from the observer O.
A point mass lens L is at distance dL from the observer:
I
x
a
S’
b
y
b
S
q
L
dLS
Observer
dL
dS
Observer sees the image I of the source S’ at an angle q from
line of sight to the lens. In the absence of deflection, would have
deduced an angle b.
Recall that all the
angles a, b, q are
small, so:
Substitute these
angles into€
expression for
deflection angle:
b
x
y
x−y
θ=
= , β= , α=
dL d S
dS
dLS
x − y 4GM
=
2
dLS
bc
4GM
θdS − βdS =
dLS
2
bc
1 4GM dLS
θ −β =
θ c 2 dS dL
Geometric factors
Quadratic equation for the apparent position of the image
q, given the true€position b and knowledge of the mass of
the lens and the various distances
Simplify this equation by defining
an angle θE, the Einstein radius :
Equation for the apparent
position then becomes:
2
2
E
θ − βθ − θ = 0
€
Solutions are:
2 GMdLS
θE =
c dL dS
2
β ± β + 4θ
θ± =
2
€
2
E
For a source exactly behind the lens, b = 0. Source
appears as an Einstein ring on the sky, with radius θE
For€
b > 0, get two images, one inside and one outside the
Einstein ring radius
Different Lensing Regimes
Conceptually simplest situation for gravitational lensing is when
the lens is massive enough to produce a large angle of deflection. Case where we can
resolve multiple images
of the background source
is called strong lensing
Einstein Ring
Einstein Cross
If the lensing is not strong enough to split the images, but it does
magnify and distort them, it is called weak lensing. This is the
effect of the large-scale structure or the outskirts of clusters of
galaxies on the background sources (galaxies). These image
distortions can then be inverted to map the mass distribution.
Weak Lensing Regime
Simulated examples of the appearance of a background field of
galaxies, with cluster-type masses in the foreground. Strong
lensing is apparent near the center. At larger radii, one has to use
statistics of image elongations and orientations
The effect of a cluster lens on a hypothetical graph paper on the
background sky
Galaxy
number
density
Light
Cluster Abell 2218
Shear
map
Mass
Squires et al. 1996
Cluster Masses From Gravitational Lensing
Strong lensing constraints:
A370
A2390
MS2137
A2218
M ~ 5x1013h-1 M
M ~ 8x1013h-1 M
M ~ 3x1013h-1 M
M ~ 1.4x1014h-1
M
M/L
~ 270h
M/L ~ 240h
M/L ~ 500h
M/L ~ 360h
Weak lensing constraints (a subset):
MS1224
A1689
CL1455
A2218
CL0016
A851
A2163
M/L
~ 800h
M/L ~ 400h
M/L ~ 520h
M/L ~ 310h
M/L ~ 180h
M/L ~ 200h
M/L ~ 300h
Lots of dark matter in
clusters, in a broad
agreement with virial
mass estimates Clusters of galaxies imply Ωdm ~ 0.1 – 0.3
Visible and DM Distribution From the
COSMOS Survey (Scoville, Massey et al. 2007)
3-D DM Distribution From the
COSMOS Survey (Massey et al. 2007)
Gravitational Microlensing
Lensing event occurs as a MAssive Compact (Halo) Object,
MACHO (could be a main sequence star, white or brown dwarf,
neutron star or black hole, or … ?), passes within an angular
distance qE of a background star:
•  background star initially brightens
•  eventually fades as the alignment is lost
MACHO crossing
the line of sight
Sun
Line of sight to a
background star
Since the cross section for a strong lensing is small compared to
interstellar separations, such events must be exceedingly rare,
Plensing ~ 10-7 /star/year. Solution: monitor ~ 107 stars
simultaneously, typically in the LMC or the Galactic Bulge
Expected
Gravitational
Microlensing
Lightcurves:
The peak magnification
depends on the lens
alignment (impact
parameter).
The event duration
depends on the lens
velocity.
Microlensing Experiments
Several experiments have searched for microlensing events:
•  toward the Galactic Bulge (lenses
are disk or bulge stars)
•  toward the Magellanic Clouds
(lenses could be stars in the LMC / SMC, or halo objects)
MACHO (Massive Compact Halo Object):
•  observed 11.9 million stars in the Large Magellanic Cloud
for a total of 5.7 years
OGLE (Optical Gravitational Lensing Experiment):
•  monitors 33 millions stars in the LMC, plus 170 million stars in the Galactic Bulge
+ many, many others
The First MACHO Event Seen
in the LMC Experiment 
To date, thousands of
microlensing events have been
detected by various groups
€
The Einstein radius for a single lens of mass M, at distance dL, observer-source distance is dS,
2 GMdLS
θE =
lens-source distance is dLS =dS- dL
c
dL dS
Probability that this lens will magnify a given source is:
$ dLS '
directly
proportional
to
P ∝θ ∝&
) × M € the mass of the lens
% d L dS (
2
E
Same is obviously true for a population of lenses, with total
mass Mpop - just add up the individual probabilities. Conclude:
•  The fraction of stars that are being lensed at any one time
measures the total mass in lenses, independent of their
individual masses
•  Geometric factors remain - we need to know where the
lenses are to get the right mass estimate
Lensing time scale: equals the physical
distance across the Einstein ring divided
by the relative velocity of the lens:
4 GMdL dLS
τ=
vLc
dS
2dLθ E
τ=
vL
Time scale is proportional to the square
root of the individual lens masses
Put in numbers appropriate for €
disk stars lensing stars in the
Galactic bulge:
•  dS = 8 kpc, dL = dLS = 4 kpc
•  M = 0.3 M
M
-1
•  vL = 200 km s τ ≈ 40
days
0.3M sun
Events with τ ~ 1 day: M < Jupiter mass (~10-3 M )
Events with τ ~ 1 year: M ~ 25 M (e.g. stellar black holes)
€
For each event, there are only two observables:
•  Duration τ - if we know the location of the lens along the
line of sight this gives the lens mass directly
•  Peak amplification A: this is related to how close the line
of sight passes to the center of the Einstein ring
b
b
Define u =
d Lθ E
A=
u2 + 2
u u2 + 4
Note: amplification tells us nothing useful about the lens!
Additionally, observing€many events gives an estimate of the
probability that a given source star will be lenses at any one time
(often called the optical depth to microlensing). This measures the
total mass of all the lenses, if their location is known.
MACHO Results
(Alcock et al. 1997)
From the number and
duration of MACHO
events, if the lenses are
in the Galactic Halo:
• 
All the mass in the halo is MACHOs is definitely ruled out
•  Typical mass is between 0.15 M and 0.9 M If the halo contains a much larger population of white dwarfs than
suspected, there are other problems: requires a major epoch of
early star formation to generate these white dwarfs – and the
corresponding metals that are not observed.
Ambiguity in the distance to the lenses is the main problem!
Distance ambiguity can be resolved in a few special cases:
a)  If distortions to the light curve
caused by the motion of the
Earth around the Sun can be
detected (parallax events)
b) If the lens is part of a binary
system. Light curves produced
by binary lenses are much more
complicated, but often contain sharp spikes (caustic
crossings) and multiple maxima.
This provides more information
about the event. (This one was
close to the SMC)
Supplementary Slides
The lens equation and the Einstein radius
Image
Source
Lens
D LS
DL
Observer
DS
Lens equation:
β =θ −α
Einstein radius:
(dimensionless)
θE =
4GM DLS
2
c DL DS
A galaxy acting as a lens:
Isothermal sphere with central singularity (SIS)
Stars considered as the particles of a perfect gas, confined by their own mean gravitational potential, with a
spherical symmetry :
ρkT
p=
m
mσ v2 = kT
dp
G M ( r ) dr
=g
2
ρ
r
equation of state
thermal equilibrium
hydrostatic equilibrium
A galaxy acting as a lens:
Isothermal sphere with central singularity (SIS)
A simple solution :
SIS
σ
1
ρ (r) =
2
2πG r
σ v2 1
Σ(ξ ) =
2G ξ
2
v
2
2
v
σ
σv

2
α = 4π
= 1.4""(
)
c
220kms −1
surface density
deflection angle
Multiple images only if the source verifies : β < θE
Solutions of the lens equation : θ± = β ± θE
A galaxy acting as a lens:
Isothermal sphere with central core (CIS)
A simple solution :
CIS
2
v
σ
1
Σ(ξ ) =
2G ξ 2 + rc2
1 + θ 02 − 1
θ0 = β0 + D
θ0
σ v2 Dd Dds
D ≡ 4π 2
c rc Ds
σ v2
1
ρ (r) =
2πG r 2 + rc2
surface density
lens equation
defines the number of images
A galaxy acting as a lens:
Isothermal sphere with central core (CIS)
β 0 = θ 0 − D[(1 + θ 02 )1 / 2 − 1] / θ 0
multiple
images
if D > 2
The local properties of the mapping source plane – lens plane are described
by its Jacobian matrix :
A ≡ ∂β /∂θ
The locus of the points θ in the lens plane where strongly disturbed images
are created is the set of points where the matrix A cannot be locally inverted, i.e., where its Jacobian is null ⇒ critical lines or caustics.
critical lines and
positions of the images
(lens plane)
caustics and
position of the source
(source plane)
Magnification
pattern due to stars
in the lensing galaxy
Surface brightness preserved :
photons neither created nor destroyed
The magnification µ is the ratio of the solid angles
of the images and of the sources, with A ≡ ∂β /∂θ
 −1
dω I
∂β
µ=
= det(  )
dω S
∂θ
1
µ=
det A
dωI+
dωI-
dωS
Convergence and shear
The local properties of the application source plane ↔ lens plane are
described by its jacobian matrix:
A ≡ ∂β /∂θ
With the convergence κ and the shear γ :
& 1 0 # & cos 2φ
A = (1 − κ )$$
!! − γ $$
0
1
%
" % sin 2φ
sin 2φ #
!
− cos 2φ !"
⇒
The convergence κ has a magnification action on the light rays:
the image conserve the shape of the source, but with a different size.
The shear induces an anisotropy with intensity γ and orientation ϕ.
Reconstruction of the mass distribution
via the gravitational distortions
Shear γ as a
function of the
convergence κ
Seitz & Schneider,
1997, A&A, 318, 687