Download Covalent Bonding

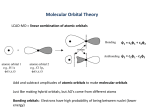
Covalent Bonding
• We seek to solve the Schrödinger equation for H2
 h2 2

− 2m ∇ + VAB (r)ψ AB (r) = Eψ AB (r)


– where VAB(r) is the intermolecular potential, which we can
approximate by writing VAB(r) = VA(r) +VB(r)
• We look for a Linear Combination of Atomic Orbitals
(LCAO) solution ...
ψ AB = cAψ A + cBψ B
– exact solution requires an infinite number of vectors
Aim of this brief treatment of covalent bonding is to illustrate what happens to
the energy levels of isolated atoms when a molecule is formed. In the coming
lectures we will see that energy levels in molecules and solids are closely
related. For simplicity we will consider the hydrogen molecule H2, for which
the energy levels, potentials and atomic wavefunctions are the same.
Consider two atoms A and B brought together from infinity. Each free atomic
orbital satisfies its own effective one-electron Schrödinger equation - in other
words, HAψA=EA and HBψA=EB
 h2 2

− 2m ∇ + VA (r)ψ A (r) = EAψ A (r)


 h2 2

− 2m ∇ + VB (r)ψ B (r) = EBψ B (r)


In practice the intermolecular potential VAB(r) depends also on electronic
wavefunction ψAB, and so the equation must be solved self-consistently.
Here we will approximate the intermolecular potential as the sum of the
individual free atomic potentials. For covalently bonded systems this is often
quite a reasonable starting approximation.
1
Hamiltonian Matrix Elements
• Our molecular Schrödinger equation looks like
(
)
h2 2
√
√
H − E (cAψ A + cBψ B ) = 0 where H = −
∇ + VAB
2m
• Premultiplying by ψA and integrating over all space yields
(hAA − E )cA + (hAB − ES)cB = 0
– where
hαβ = ∫ ψ α H√ψ β dr
S = ∫ ψ Aψ B dr
The slightly unusual looking eigenvalue equation is simply a rearrangement of
the more familiar
H√ψ = Eψ
Manually do the premultiply by ψA. Since s-orbitals are real we can forget
about using the complex conjugate.
Since we are considering the hydrogen molecule we can definitively assert that
the overlap S is a positive number, as the wavefunctions are real and do not
change sign
For higher angular momenta combinations (and higher principal quantum
numbers) the integrals depend on the atomic separation due to the change in
sign of the wavefunction with radius and direction.
The same procedure using ψB yields
(hBA − ES)cA + (hBB − E )cB = 0
2
Matrix Equation
• A similar premultiplication by ψB and the approximation
that the overlap S is zero yields the matrix equation
hAB  cA 
hAA − E
=0
 h
hBB − E  cB 
 BA
• Diagonal elements
(
)
hAA = ∫ ψ A H√ A + VB ψ A dr = EA + ∫ ρ AVB dr ≈ EA
• Off-diagonal elements
(
)
hAB = ∫ ψ A H√B + VA ψ B dr = ∫ ψ AVAψ B dr = − β
The Matrix
Make the approximation that the overlap S is equal to zero.
Simplifies the mathematics, without affecting the qualitative description. The
case of finite S is a relatively simple algebraic exercise.
Diagonal Elements
Write HAB= HA + VB
The integral over ρA reflects a small lowering in the energy of the electron on
atom A due to the attractive tail of the potential from atom B. Again, for
simplicity of argument we will ignore this term. The same approach applies to
the other diagonal element hBB.
Off-diagonal Elements:
This time we express HAB as HB + VA. Get integral ψAHBψB=ψAEBψB=ES
With the neglect of overlap this term vanishes. β is unambiguously +’ve
By symmetry, the two off-diagonal elements are equal (for complex
wavefunctions, the off-diagonal elements are complex conjugates).
3
Eigenvalues and Eigenvectors
• Determinant must be zero for non-trivial solutions
E0 − E
−β
−β
=0
E0 − E
• The eigenvalues and eigenvectors are
 E0 − β
E=
 E0 + β
(c A = cB )
(c A = − cB )
• To first order, the inclusion of a finite overlap S yields
E = E0 + βS ± β
Setting the determinant equal to zero yields
( E0 − E )2 − β 2 = 0
E0 − E = ± β
E = E0 ± β
For E=E0–β the values of cA and cB are determined by solving
β
− β

− β  c A 
=0
β  cB 
⇒
c A = cB
⇒
c A = − cB
Similarly, for E=E0+β, we have
− β
− β

− β  c A 
=0
− β  cB 
The quantity β is referred to as the bond integral
Overlap repulsion is reflected in the term βS
4
Energy Levels and Molecular Orbitals
• The free atom orbitals combine to form bonding and antibonding states separated in energy by an amount 2β
E0
2β
• The upper molecular state (with the anti-symmetric wavefunction) does not
lead to bonding as it’s energy is higher than the energy of the free atoms. It is
known as the anti-bonding state.
• The lower molecular state (with the symmetric wavefunction) does lead to
bonding as it’s energy is lower than the separated atoms. It is called the
bonding state. Note that the lowering of the energy is given by β which
explains why we called this quantity the bond integral.
• From the previous slide we see that the molecular eigenvalues are shifted
upwards by an amount βS due to overlap repulsion which reflects the Pauli
exclusion principle. These are the two key ingredients of the covalent bond:
an attractive bond energy pulling the atoms together, balanced at equilibrium
by a repulsive overlap potential keeping the atoms apart.
• We compute charge density for these two states by taking the square of the
respective wavefunctions which shows that the anti-bonding state has zero
electron density at the midpoint of the two points, whereas the bonding state
has a heaping up of charge which is attracted to both nuclei and thus by
electrostatics pulls the nuclei together.
5
Beyond the Hydrogen Molecule
• He-He molecule (unstable)
– populate bonding and anti-bonding levels, and the average
energy is unchanged (in fact, slightly higher)
• Li-Li molecule (stable)
– 1s orbitals much close to nucleus than 2s orbitals
– very small splitting for 1s levels
– bonding arises from the 2s energy split
• Be-Be molecule (unstable)
– populated bonding and anti-bonding for 2s energy split, and
so the average energy is unchanged
We can study this numerically using a pair of square-well-potentials. It is very
instructive to compute the energy difference numerically and compare it to the
bond integral β. A very attractive aspect of this approach is that we can
understand the bond integral b using a one-dimensional integral. Note that the
energy split does not reflect simply the overlap between the free-atom
wavefunctions - rather, it is integral involving the product of the two
wavefunctions and the free-atom potential.
6