Download Laser Molecular Spectroscopy CHE466 Fall 2007

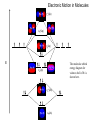
Laser Molecular Spectroscopy
CHE466
Fall 2009
David L. Cedeño, Ph.D.
Illinois State University
Department of Chemistry
Electronic Spectroscopy
Electronic Motion
Electron Motion: Orbital and Spin Angular Momentum
Consider one electron in the hydrogen atom. Depending on its energy, electron motion is restricted
to certain regions of space in a probabilistic manner. The waveunction associated to such
probability is called an orbital. The particular “position” of an electron is dependent on its orbital
angular momentum, which is a quantized property (with quantum number l, which depends on
principal quantum number n).
Magnitude of orbital angular momentum: [l (l  1)]
for l = 0, 1, 2, …(n-1)
Since an electron is charged, then its motion also generate a magnetic momentum called the spin
angular momentum. The spin angular momentum is also quantized.
Magnitude of spin angular momentum: [ s ( s  1)] for s = ±1/2
Thus the total angular momentum of an electron is the sum of both orbital and spin angular
momentum.
Magnitude of total angular momentum: [ j ( j  1)]for j = l+s, l+s-1, …|l-s|
Electronic Motion
Electron Motion: Orbital and Spin Angular Momentum
For multiple electrons in an atom, the angular momentum is defined by the sum of the angular
momentum of the individual electrons, but bear in mind that angular momentum are vectors.
Example: Find the angular momentum of an excited state of Helium corresponding to electron
configuration 1s1 2p1
The total orbital momentum L = l1 + l2, l1 + l2 – 1, …, |l1 – l2| = 1 + 0 = 1
The total spin momentum S = s1 + s2, s1 + s2 – 1, …, |s1 – s2| = ½ + ½, ½ - ½ = 1, 0
The total angular momentum J = L + S, L + S – 1, …, |L – S| = 2, 1, 0 for L = 1 and S = 1; and 1 for
L = 1, S = 0.
Electron Motion: Spectroscopic Term Symbols
A term symbol is used to identify a given electronic state with a given electron configuration in
terms of the angular momentum. For an atom it corresponds to:
2S+1L
J
For the example above there are 4 electronic states associated to 1s1 2p1 configuration: 3P2, 3P1, 3P0
corresponding to the S = 1 (called triplet states) and 1P1 for that with S = 0 (a singlet state)
Electronic Motion
Electron Motion: Angular Momentum and Energy
Hund rules determine the energy ordering of the states of a given electron configuration. These
state that for an atom:
1. If the states have the same orbital angular momentum (L), then the one with the greatest spin
angular momentum (S) has the lowest energy
2. If two states have the same spin angular momentum (S), then the one with the largest orbital
angular momentum (L) has the lowest energy
3. The ordering in terms of J for a given term depends on whether an electron shell is less or
more than half-full. For a less than half-full, the one with the lowest J is the lowest energy, for
more than half-full, the one with the highest J is the lowest energy.
In the previous example:
3P
0
< 3P1 < 3P2 < 1P1
Electronic Motion in Molecules
Diatomic Molecules: Molecular Orbital Theory
The calculation of the energy of a molecule using the Schrodinger equation is complicated by the
fact that a molecule contains more than one electron that is somehow shared at different extents by
a set of nuclei. In addition, the interaction between electrons is difficult to represent. These
problems translate in our inability to solve the Schrodinger equation exactly for a molecule.
Furthermore, suitable molecular wavefunctions are not easy to find.
Molecular orbital theory is a successful approach to obtain the energy of molecular electronic
states which utilizes the variational principle to obtain the energy of molecular wavefunctions (i.e.
orbitals) that are built as linear combinations of atomic orbitals (i.e. hydrogen-like wavefunctions).
Let us illustrate this methodology with the H2 molecule. Each atom contributes one 1s orbitals to
the molecular wavefunctions. As a rule of thumb, the number of molecular orbitals (MOs) obtained
is equal to the number of atomic orbitals (AOs) combined. These AOs are combined algebraically:
For H2: Y = Sci(1s)i Therefore there will be two MOs resulting from the combination of 2 1s
AOs.
Electronic Motion in Molecules
Diatomic Molecules: Molecular Orbital Theory
The variational principle is used to obtain the energy: in this case the expectation value of the
energy is obtained on the basis of the optimization of the coefficients (ci) in a way that the
minimum possible energy is obtained. This process is usually known as energy minimization. The
expectation value of the energy E is:
Y Hˆ Yd  [(c1 (1s )1  c2 (1s) 2 ) Hˆ (c1 (1s)1  c2 (1s ) 2 )]d

E

*
*
Y
Y
d


 [(c1(1s)1  c2 (1s) 2 ) (c1(1s)1  c2 (1s) 2 )]d
[c12 (1s )1* Hˆ (1s)1  c1c2 (1s )1* Hˆ (1s) 2  c2c1 (1s )*2 Hˆ (1s )1  c22 (1s )*2 Hˆ (1s) 2 ]d

E
2
*
*
2
*
 [c1 (1s)1 (1s)1  2c1c2 (1s)1 (1s) 2  c2 (1s) 2 (1s) 2 ]d
*
*
Since AO’s are normalized and the Hamiltonian is a Hermitian operator then:
 (1s)1 (1s)1 d  (1s)2 (1s)2 d  1
*
*
 (1s)1 Hˆ (1s)2 d   (1s)2 Hˆ (1s)1 d  H12
*
And the quantity
*
 (1s)1 (1s)2 d  (1s)2 (1s)1 d  S12
*
*
Electronic Motion in Molecules
Diatomic Molecules: Molecular Orbital Theory
The expectation value of the energy E can be written as:
E
Using the variational principle:
c12 H11  2c1c2 H12  c22 H 22
c12  2c1c2 S12  c22
 E 

  0
 ci  j i
It is possible to have a system of equations that allow us to obtain the energy and coefficients. For
this example:
c1 ( H11  E )  c2 ( H12  ES12 )  0
c1 ( H12  ES12 )  c2 ( H 22  E )  0
or
H11  E
H12  ES12
H12  ES12
H 22  E
0
Electronic Motion in Molecules
Diatomic Molecules: Molecular Orbital Theory
This determinant yields a quadratic equation on E with solutions:
E 
a b
1 S
a  H ii
b  H ij
S  Sij
b is called the resonance integral and has a negative value. a is the Coulomb integral. Thus, the state
with E– = (a – b)/(1 – S) is higher in energy than the other one with energy E+ = (a + b)/(1 + S). Note
that For the hydrogen molecule a is equal to the energy of a hydrogen atom (a = EH)
The coefficients can be obtained from the equations (called secular) and the fact that:
c12  c22  1
If we assume S = 0, the wavefunction of the MO with the lower energy has c1 = c2 = √2/2 and the
wavefunction for the highest energy has c1 = –c2 = √2/2.
Electronic Motion in Molecules
Diatomic Molecules: Molecular Orbital Theory
The molecular orbital energy diagram for H2 is shown below:
su*(1s)
a–b
E
a
ab
sg(1s)
Electronic Motion in Molecules
su*(2p)
pg*(2p)
sg(2p)
E
The molecular orbital
energy diagram for
valence shell of N2 is
shown here.
pu(2p)
su*(2s)
sg(2s)
Electronic Motion in Molecules
Diatomic Molecules: Molecular Orbital Theory
The order of MOs as a function of energy for Li2, Be2, C2 and N2 is:
sg(2s) < su*(2s) < pu(2p) < sg(2p) < pg*(2p) < su*(2p)
But this is changed for O2, F2 and Ne2:
sg(2s) < su*(2s) < sg(2p) < pu(2p) < pg*(2p) < su*(2p)
The bond order is related to the strength of the molecule and their relative stability:
BO 
# bonding electrons - # antibondin g electrons
2
Electronic Motion in Molecules
Diatomic Molecules: States and Term Symbols
Consider the ground state configuration of N2:
[He2]sg(2s)2 su*(2s)2 pu(2p)4 sg(2p)2
The total spin (S) is zero, so it is a singlet (2S + 1 = 1). The total orbital angular momentum is also zero.
In order to assign the term symbol we utilize the symmetry symbols of the HOMO via the cross product:
sg x sg = sg. The term symbol is 1Sg+.
Consider the excited state: [He2]sg(2s)2 su*(2s)2 pu(2p)4 sg(2p)1 pg*(2p)1:
sg x pu = pu. However, there are two possible spin multiplicities 1 and 3 (for S = 0 and 1 respectively).
There is also the possibility of adding the spin and orbital angular momentum, which carries out a split
of the energy of the possible states for such an electron configuration. The sum of these angular
momentum defines a total angular momentum J (called W). For this configuration J = L + S, L + S -1, …,
|L – S|. = 1. For the triplet state: J = 2, 1, and 0; for the singlet state: J = 1. The term symbols are: 1Pu,
3P , 3P , 3P . Thus four excited states are linked to the electron configuration above. Hund’s rule
u,2
u,1
u,0
still follows.
Electronic Motion in Molecules
Diatomic Molecules: States and Term Symbols
Consider the following electron configuration of O2:
[He2]sg(2s)2 su*(2s)2 sg(2p)2 pu(2p)4 pu*(2p)2
In this case there are two electrons in two degenerate MOs. The cross product is pg x pg = Sg+ + Sg- + Dg
The spin multiplicity is singlet or triplet, however Pauli’s exclusion principle forbids two of the possible
triplet state. The only allowed triplet state is the ground state (Hund’s rules) with a term symbol is 3Sg-.
The negative parity is a consequence of the antisymmetric nature of the electronic wavefuction.
Pauli’s exclusion principle excludes the states with symbols: 3Sg+ and 3Dg. The antisymmetric nature of
the electronic wavefunction also excludes the singlet with term symbol 1Sg-.
This, there are three states for the configuration above: 3Sg- (ground state), 1Dg, and 1Sg+. The 1Dg state is
7882.39 cm-1 above the ground state, while the 1Sg+ is 13120.91 cm-1 above.
pg*
pg*
3S g
pg*
pg*
1S +
g
pg*
1D
pg*
g
Electronic Motion in Molecules
Diatomic Molecules: States and Term Symbols
Another example, NO:
Ground state: [He2]s(2s)2 s*(2s)2 s(2p)2 p(2p)4 p*(2p)1
In this case there is one unpaired electrons in two degenerate MOs. There is no need for cross product,
the ground state has a P term symbol The total spin is ½, thus the state is a doublet. The total angular
momentum (spin + orbital) could be (1 + ½) or (1 – ½), that is W = 3/2 and ½. The ground state of NO is
the one with the lowest W, thus it has the symbol: 2P1/2. The other state (2P3/2) is only 119.73 cm-1 above
the ground state, indicating a small coupling of the spin and orbital momentum. With such a small
separation both states are populated at room temperature (see selection rules later).
Electronic Motion in Molecules
Diatomic Molecules: Selection Rules
Whether an electronic transition is allowed depends on the effect of changing the total angular
momentum of the molecule as the induced dipole couples with the photons:
1. DL = 0, ±1 is allowed
2. DS = 0 is allowed (exception to the rule in heavy diatomics like I2, where DS = 1 is allowed)
3. DW = 0, ±1 is allowed
4. For S to S transitions: + ↔ + and – ↔ – are allowed
5. For homonuclear diatomics: g ↔ u is allowed
6. For molecules containing heavy atoms: regarding the states with W = 0, 0 + ↔ 0+ and 0– ↔ 0– are
allowed.
Example: Would the transition from O2 ground state (3Sg-) to its first excited state (1Dg) be allowed?
No because DL = 2 (S to D transition), and DS = 1. This is a doubly forbidden transition. Also it violates
the inversion selection rule because g ↔ g.
Example: Would the transition from I2 ground state (1Sg+) to its second excited state (3Pu) be allowed?
Yes because DL = 1 (S to P transition) and DS = 1 is now allowed (strong spin-orbital coupling). The
inversion rule is also allowed g ↔ u. The last rule could also be considered here, the complete term
symbol for the excited state is 3P0u+, thus 0+ ↔ 0+ also holds.
Electronic Motion
Diatomic Molecules: Vibrational coupling
The following shows the visible spectrum of I2 at a resolution of 0.02 nm.
Iodine Gas Absorption Spectrum
0.25
0.24
0.2
Absorbance
0.22
0.15
0.2
0.1
540
0.18
550
0.16
560
570
580
590
Wavelength (nm)
0.14
0.12
0.1
490
510
530
550
570
590
610
630
650
Wavelength (nm)
The transition corresponds to the (1Sg+ → 3Pu) transition. The bands observed are the result of
changes in the vibrational motion that are concomitant to the changes in electronic motion. Overall
there are three band progressions, with transitions originating at v” = 0, 1, and 2.
Electronic Motion
The Franck-Condon Principle
The probability of a vibrational transition is dictated by the relative overlap of the potential energy
surfaces and the overlap of the vibrational wavefunctions at a particular internuclear distance in the
lower electronic state. In essence, the electronic transition occurs before the nuclei move (in other
words, from the perspective of electron motion, nuclei are stationary).
Quantum mechanically, the probability is
associated to:
Rev   e *' v *' ˆ e " v " d e dr
Rev   v *' Re v "dr
Rev  Re  v *' v "dr
Rev   e *' v *' ˆ e " v " d e dr
Rev   v *' Re v "dr
Rev  Re  v *' v "dr
The square of the quantity  v *' v "dr
is the Franck-Condon factor of the transition
Electronic Motion
Franck-Condon Principle and Band Shape
The effect of the electronic transition on the internuclear distance is important in terms of the
probability of the vibrational transitions and band shapes.
Electronic Motion in Molecules
Diatomic Molecules: Molecular Constants and Dissociation Energies from Spectra
It is possible to obtain the dissociation energy from the spectrum by carrying out a combination of
differences within a given band progression (i.e. constant v” or v’). In this case the difference
between two consecutive bands (with vibrational numbers v’ and v’+1) belonging to a given
progression (say v” = 0) is plotted against the value of v’+1. It can be shown that such difference
is:
G(v’+1)-G(v’) = we’ – 2we’xe’(v’+1)
Similarly for two bands with vibrational number v” and v”+1 that belong to the same progression
(same v’):
Birge-Sponer Plot B state of I2
G(v”)-G(v”+1) = we” – 2we”xe”(v”+1)
140
y = -1.9964x + 133.07
R2 = 0.9984
The dissociation energy relative to the
v’= 0 (zpe), D0, is the area under
the line from v’+1 = 1 to the max v’+1
G(v'+1) - G(v')
120
100
80
60
40
20
0
0
10
20
30
40
v' + 1
50
60
70
80
Electronic Motion in Molecules
Diatomic Molecules: Bond Dissociation Energies from Spectra
Electronic Motion in Molecules
Polyatomic Molecules: Molecular Orbital Theory
It is possible to extend the treatment of the LCAO and variational principle to any molecule.
Indeed most computational software in the market does this to provide the energy of the orbitals
and the contribution of atomic orbitals.
Application: AH2 molecules: This can be bent (C2v) or linear (D∞h). In any case the valence MOs
are built from the combination of the 1s orbitals of the H atoms and the ns and np orbitals of the A
atom. If the molecule were linear the MOs would be labeled according to the symmetry
representation (using the greek symbols), but once the molecule is bent the MOs are named using
the a1, a2, b1 or b2 symmetry symbols from the C2v group.
The MOs in both geometries are correlated via a Walsh diagram (see next page)
Electronic Motion in
Molecules
Walsh Diagram for HAH Molecule (not at scale)
2b2
2su
[1s(H) - 2pz(A) - 1s(H)]
4a1
3sg
[1s(H) -2s(A) + 1s(H)]
pu
1b1
Energy
Example:
BeH2 is though to have a
linear ground state, with 4
valence electrons, the
electron configuration is
(2sg)2(1su)2. Term symbol
is 1Sg+.
The first excited state is
bent with electron
configuration
(2a1)2(1b2)1(3a1)1. The
possible term symbols are
3B and 1B .
2
2
[1s(H) + 2px(A) + 1s(H)]
1b2
3a1
[1s(H) + 2py(A) + 1s(H)]
1su
[1s(H) + 2pz(A) - 1s(H)]
2a1
2sg
[1s(H) + 2s(A) + 1s(H)]
CHE466 – D. Cedeno
90o
180o
Electronic Motion in Molecules
Example: Formaldehyde.
A MO treatment yields the frontier
MOs shown. The MOs are labeled
according to the symmetry
representation (C2v). The energy
ordering is 1b1 < 2b2 < 2b1.
The ground state is 1A1 (b2 x b2).
The lowest energy transition
corresponds to a HOMO to LUMO
electronic motion. This transition is
common in carbonyl containing
compounds and is called a n → p*
transition. This transition results in
two excited states (triplet and singlet)
with the same term symbol: A2, thus
the 3A2 and 1A2 excited states.
2b1: LUMO
(non bonding)
(A p* MO)
2b2: HOMO
(non bonding)
1b1: HOMO-1
(a p MO)
Electronic Motion in Molecules
The Huckel MO Method
For conjugated molecules involving valence MOs that originate from pure p AOs, the
Huckel method provides a simplified, yet satisfactory modeling ot the MOs. The Huckel
method considers a LCAO of pz orbitals from atoms that participate in the conjugation.
The secular determinant is given by:
H11  E
H 21  ES12

H n1  ESn1
H12  ES12

H1n  ES1n
H 22  E
 H 2n  ES2n
0


H n 2  ESn 2 
H nn  E
The following approximations apply:
1. For any Smn, if m ≠ n, then Smn = 0, if m = n, then Snm = 1
2. Any Hnn = a (Coulomb integral)
3. Any Hmn = b (resonance integral) only if m and n are adjacent (i.e. atoms are bonded),
while Hmn = 0 for atoms that are not bonded.
Electronic Motion in Molecules
Example: Benzene
The secular determinant for benzene is:
a E
b
0
0
0
b
b
a E
b
0
0
0
0
b
a E
b
0
0
0
0
0
b
a E
b
0
0
0
0
b
a E
b
b
0
0
0
b
a E
which can be written as after making x 
αE
β
x 1 0 0 0 1
1 x 1 0 0 0
0
0
0
1
1 x 1 0 0
0
0 1 x 1 0
0 0 1 x 1
0 0 0 1 x
Solutions are x = ±2, ±1, ±1, or E1 = a + 2b, E2 = E3 = a + b, E4 = E5 = a – b, E6 = a – 2b.
Electronic Motion in Molecules
Example: Benzene
The MOs are represented by a LCAO: Yi = Scii(pz). Six pz AOs produce six MOs.
Y6 (b2g)
Y5 (e2u)
Y4 (e2u)
Y2 (e1g)
Y3 (e1g)
Y1 (a2u)
Images courtesy of http://chemical-quantum-images.blogspot.com/2007/01/benzenes-mos.html
Electronic Motion in Molecules
Selection Rules in Polyatomic Molecules
Electronic motion is highly allowed in polyatomic molecules. The one rule that hold is the
one concerning to the change in the spin angular momentum:
DS = 0 (for low spin-orbital coupling)
The selection rules of a polyatomic molecule depends on symmetry properties of the
electronic wavefunctions. In terms of transition that depend on the coupling of light with the
electric dipole moment (), the rules is:
Г(Yel’) x Г() x Г(Yel”) ⊇ A
or
Г(Yel’) x Г(Tx) x Г(Yel”) ⊇ A
Г(Yel’) x Г(Ty) x Г(Yel”) ⊇ A
Г(Yel’) x Г(Tz) x Г(Yel”) ⊇ A
Which is then written as:
Г(Yel’) x Г(Yel”) ⊇ Г(Tx)
Г(Yel’) x Г(Yel”) ⊇ Г(Ty)
Г(Yel’) x Г(Yel”) ⊇ Г(Tz)
Electronic Motion in Molecules
Selection Rules in Polyatomic Molecules
Example: The ground state of benzene has a term symbol 1A1g. Determine if the transition to
the excited state 1B1u is allowed.
Cross product: A1g x B1u = B1u. For D6h, Г(Tz) = A2u and Г(Tx,Ty) = E1u. Since the cross
product of the symmetry labels of the excited state does not contain any of the symmetry
representations for translation, the transition is NOT allowed.
Note that in order to have a transition from the ground state in benzene, the excited state
must be a 1A2u, or 1E1u.
Electronic Motion in Molecules
Diffuse Spectra and Photophysical Processes
The UV-Vis spectra of polyatomic molecules (even in the gas phase) is mostly composed of
very broad bands. The reason being that many vibrational (and rotational) transitions concur
in a relatively small range of frequencies that correspond to the electronic transition.
This spectrum of pyrene shows 3
distinctive bands, in which some
vibrational progressions are
evident. The ground state of
pyrene (D2h) is 1Ag, with allowed
transitions into 1B1u and 1B2u and
1B excited states.
3u
In cyclohexane solution, Du et al, Photochem.
Photobiol. 1998, 68, 141
Electronic Motion in Molecules
Photophysical Processes
IC
Absorption
M1
Fluorescence
1
Radiative Processes
Fluorescence: Light emission DS = 0
Phosphorescence: Light emission DS
=1
3
1
M0
M1
Non-Radiative Processes
Internal Conversion: heat release via
vibrational relaxation induced by
collisions (DS = 0)
Intersystem Crossing: heat release as
a result of a spin-orbital change
induced by internal or external factors
(DS = 1)
Electronic Motion in Molecules
Photophysical Processes
Quantum Yields: In any process initiated by light, the quantum yield is the efficiency of the
process per every 100 photons absorbed. For example, a 0.12 fluorescence quantum yield
means that out of 100 photons absorbed by the compound, 12 of them are converted into
emitted photons.
The quantum yield of a photophysical process depends on the relative rates of competing
processes. For example the fluorescence quantum yield is defined as:
f 
kf
k f  k IC  k ISC
Where the kf, kISC and kIC are the rate constants for fluorescence, intersystem crossing and
internal conversion respectively. Note that the sum of these rate constants represent the rate
constant for decay of the excited singlet state.
The rates of photophysical processes and therefore the quantum yields are thus dependent on
the structure of the compound and the molecular environment around it.
Photophysical Processes: Effects of excitation on molecular structure
From N. Turro, Modern Molecular Photochemistry, 1st Ed, 1978
Photophysical Processes: Chromophores and Orbital Configurations (Typical)
From N. Turro, Modern Molecular Photochemistry, 1st Ed, 1978
Photophysical Processes: Effect of Environmental Conditions
From N. Turro, Modern Molecular Photochemistry, 1st Ed, 1978
Photophysical Processes: Effect of Environmental Conditions
From N. Turro, Modern Molecular Photochemistry, 1st Ed, 1978
Photophysical Processes: Effect of Environmental Conditions
From N. Turro, Modern Molecular Photochemistry, 1st Ed, 1978