Download Topic 16 Notes 16 Eigenvalues, diagonalization, decoupling Jeremy Orloff

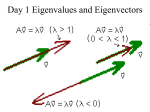
Topic 16 Notes
Jeremy Orloff
16 Eigenvalues, diagonalization, decoupling
This note covers topics that will take us several classes to get through. We will look
almost exclusively at 2 × 2 matrices. These have almost all the features of bigger
square matrices and they are computationally easy.
16.1 Etymology:
This is from a Wikipedia discussion page. The word eigen in German or Dutch
translates as ’inherent’, ’characteristic’, ’private’. So eigenvector of a matrix is
characteristic or inherent to the matrix. The word eigen is also translated as ’own’
with the same sense as the meanings above. That is the eigenvector of a matrix is
the matrix’s ’own vector’.
In English you sometimes see eigenvalues called special or characteristic values.
16.2 Definition
For a square matrix M an eigenvalue is a number (scalar) λ that satisfies the equation
M v = λ v for some non-zero vector v.
(1)
The vector v is called an eigenvector corresponding to λ. We will call equation
(16.3) the eigenvector equation.
Comments:
1. Using the symbol λ for the eigenvalue is a fairly common practice when looking
at generic matrices. If the eigenvalue has a physical interpretation we’ll often use a
corresponding letter. For example, in population matrices the eigenvalues are growth
rates, so we’ll often denote them using r or k.
2. Eigenvectors are not unique. That is, if v is an eigenvector with eigenvalue λ then
so is 2 v, 3.14 v, indeed so is any scalar multiple of v.
16.3 Why eigenvectors are special
6 5
Example 16.1. Let A =
.
1 2
We will explore how A transforms vectors and what makes an eigenvector special. We
will see that A scales and rotates most vectors, but only scales eigenvectors. That is,
eigenvectors lie on lines that are unmoved by A.
1
16 Eigenvalues, diagonalization, decoupling
1
6
0
5
Take u1 =
⇒ Au1 =
; Take u2 =
⇒ Au2 =
.
0
1
1
2
We see that A scales and turns most vectors.
5
35
Now take v1 =
⇒ Av1 =
= 7v1 .
1
7
The eigenvector is special since A just scales it by 7.
1
Likewise, v2 =
then Av2 = v2 .
−1
The eigenvector v2 is really special, it is unmoved by A.
y
Au2
2
to Av1 = (35, 7)
v1
u2
Au1
u1
-1
2
4
6
x
v2 = Av2
Example (16.3): Action of the matrix A on vectors
1
1
Example 16.2. Suppose A is a 2 × 2 matrix that has eigenvectors
and
2
3
with eigenvalues 2 and 4 respectively.
1
(a) Compute A
.
2
1
answer: Since
is an eigenvector this follows directly from the definition of eigen2
1
1
2
vectors: A
=2
=
.
4
2
2
1
1
(b) Compute A
+
.
2
3
answer: This uses the definition of eigenvector plus linearity:
1
1
1
1
1
1
6
A
+
=A
+A
=2
+4
=
.
2
3
2
3
2
3
16
2
16 Eigenvalues, diagonalization, decoupling
1
1
(c) Compute A 3
+5
.
2
3
answer: Again this uses the definition of eigenvector plus linearity:
1
1
1
1
1
1
26
A 3
+5
= 3A
+ 5A
=6
+ 20
=
.
2
3
2
3
2
3
72
0
(d) Compute A
.
1
0
into eigenvectors:
answer: We first decompose
1
0
1
1
=
−
.
1
3
2
Now we can once again use the definition of eigenvector plus linearity:
0
1
1
1
1
1
1
2
A
=A
−
=A
−A
=4
+2
=
.
1
3
2
3
2
3
2
8
Example 16.3. Any rotation in three dimensions is around some axis. The vector
along this axis is fixed by the rotation, i.e. it is an eigenvector with eigenvalue 1.
16.4 Computational approach
In order to find the eigenvectors and eigenvalues we recall the following basic fact
about square matrices.
Fact: The equation M v = 0 is satisfied by a non-zero vector v if and only if det(M ) =
0. (Said differently, the null space of M is non-trivial exactly when det(M ) = 0.)
First we manipulate the eigenvalue equation (1) so that finding eigenvectors becomes
finding a null vectors:
A v = λ v ⇔ A v = λ Iv ⇔ A v − λ Iv = 0 ⇔ (A − λ I)v = 0.
Now we can apply our ’fact’ to the last equation above to conclude that λ is an
eigenvalue if and only if
det(A − λ I) = 0
(2)
(Recall that an definition of eigenvalue requires v to be non-zero.)
We call equation (2) the characteristic equation. (Eigenvalues are sometimes called
characteristic values.) It allows us to find the eigenvalues and eigenvectors separately
in a two step process.
3
16 Eigenvalues, diagonalization, decoupling
Notation:
For simplicity we will use the notation |A| = det(A).
Eigenspace: For an eigenvalue λ the set of all eigenvectors is none other than the
nullspace of A − λI. That is, it is a vector subspace which we call the eigenspace of
λ.
6 5
Example 16.4. Find the eigenvalues and eigenvectors of the matrix A =
.
1 2
answer: Step 1: Find the eigenvalues λ: |A − λI| = 0 (characteristic equation)
6 5
6 − λ
λ 0 5 −
⇒ =0 ⇒ = 0.
1 2
0 λ 1
2 − λ
⇒ (6 − λ)(2 − λ) − 5 = λ2 − 8λ + 7 = 0 ⇒ λ = 7, 1.
Step 2: Find the eigenvectors v: (A − λI)v = 0.
a1
Let v =
.
a2
−1 5
a1
0
5
λ1 = 7:
=
⇒ −a1 + 5a2 = 0. Take v1 =
.
1 −5
a2
0
1
5 5
a1
0
1
λ2 = 1:
=
⇒ 5a1 + 5a2 = 0. Take v2 =
.
1 1
a2
0
−1
To repeat the comment above, any scalar multiple of these eigenvectors is also an
eigenvector with the same eigenvalue.
Trick. In the 2 × 2 case we don’t have to write out the matrix equations for a1 and
a2 . Notice that the entries in our eigenvectors come from the entries in one row of
the matrix. You use the right entry of the row and minus the left entry. If you think
about this a moment you’ll see that it is always the case. (But don’t use a row of all
zeros.)
Matlab: In Matlab the function eig(A) returns the eigenvectors and eigenvalues of
a matrix.
Complex eigenvalues
If the eigenvalues are complex then the eigenvectors are complex. Otherwise there is
no difference in the algebra.
3 4
Example 16.5. Find the eigenvalues and eigenvectors of the matrix A =
.
−4 3
answer: Step 1: Find the eigenvalues λ: |A − λI| = 0 (characteristic equation)
3 4
3 − λ
λ
0
4
=0 ⇒ ⇒ −
−4 3 − λ = 0.
−4 3
0 λ ⇒ (3 − λ)2 + 16 = 0 ⇒ λ = 3 ± 4i.
Step 2, Find the eigenvectors v:
(A − λI)v = 0.
4
16 Eigenvalues, diagonalization, decoupling
λ1 = 3 + 4i:
λ2 = 3 − 4i:
1
−4i 4
.
v = 0. Take v1 =
−4 −4i 1
i
4i 4
1
v2 = 0. Take v2 =
.
−4 4i
−i
Notice that the eigenvalues and eigenvectors come in complex conjugate pairs. Knowing this there is no need to do a computation to find the second member of each pair.
1 −4
Example 16.6. Find the eigenvalues and eigenvectors of the matrix A =
.
5 5
answer: Step 1: find λ (eigenvalues): |A − λI| = 0 (characteristic equation)
1 − λ −4 = 0 ⇒ λ2 − 6λ + 25 = 0 ⇒ λ = 3 ± 4i.
⇒ 5
5 − λ
Step 2, find v (eigenvectors): (A − λI)v = 0.
−2 − 4i −4
4
λ1 = 3 + 4i:
v = 0. Take v1 =
.
5
2 − 4i 1
−2 − 4i
4
.
λ2 = 3 − 4i: take v2 = v1 =
−2 + 4i
Repeated eigenvalues
When a matrix has repeated eigenvalues the eigenvectors are not as well behaved as
when the eigenvalues are distinct. There are two main examples
Example 16.7. Defective case
3 1
Find the eigenvalues and eigenvectors of the matrix A =
.
0 3
answer: Step 1: Find the eigenvalues λ: |A − λI| = 0 (characteristic equation)
3 − λ
1 ⇒ = 0 ⇒ (λ − 3)2 = 0 ⇒ λ = 3, 3.
0
3 − λ
Step 2, Find the eigenvectors v: (A − λI)v = 0.
0 1
1
λ1 = 3:
v = 0. Take v1 =
.
0 0 1
0
There are no other eigenvalues and we can’t find another independent eigenvector
with eigenvalue 3. We have two eigenvalues but only one independent eigenvector, so
we call this case defective or incomplete
In terms of eigenspaces and dimensions we say the repeated eigenvalue λ = 3 has a
one dimensional eigenspace. It is defective because we want two dimensions from a
double root.
Example 16.8.
Complete case Find the eigenvalues and eigenvectors of the
5
16 Eigenvalues, diagonalization, decoupling
3 0
matrix A =
.
0 3
answer: Step 1: Find the eigenvalues λ: |A − λI| = 0 (characteristic equation)
3 − λ
0
= 0 ⇒ (λ − 3)2 = 0 ⇒ λ = 3, 3.
⇒ 0
3 − λ
Step 2, Find the eigenvectors v: (A − λI)v = 0.
0 0
λ1 = 3:
v = 0.
0 0 1
This equation shows that every vector in R2 is an eigenvector. That is, the eigenvalue
λ = 3 has a two dimensional
eigenspace.
We
can pick any two independent vectors
1
0
as a basis, e.g. v1 =
and v2 =
. If we preferred we could have chosen
0
1
6
5
v1 =
and v2 =
. Because we have as many independent eigenvectors as
1
2
eigenvalues we call this case complete.
16.5 Diagonal matrices
In this section we will see how easy it is to work with diagonal matrices. In later
sections we will see how working with eigenvalues and eigenvectors of a matrix is like
turning it into a diagonal matrix.
2 0
Example 16.9. Consider the diagonal matrix B =
0 3
u
2u
Convince yourself that B
=
. That is B scales the first coordinate by 2
v
3v
and the second coordinate by 3.
We can write this as
1
1
0
0
B
=2
and B
=3
0
0
1
1
1
0
This is exactly the definition of eigenvectors. That is,
and
are eigenvectors
0
1
with eigenvalues 2 and 3 respectively. That is, for a diagonal matrix the diagonal
entries are the eigenvalues and the eigenvectors all point along the coordinate axes.
16.6 Diagonal matrices and uncoupled algebraic systems
Example 16.10. An uncoupled algebraic system Consider the system
7u
= 1
v = −3
6
16 Eigenvalues, diagonalization, decoupling
This barely deserves to be called a system. The variables u and v are uncoupled and
we solve the system by finding each variable separately: u = 1/7, v = −3.
Example 16.11. Now consider the system
6x + 5y = 2
x
In matrix form this is
+ 2y = 4.
6 5
x
2
=
1 2
y
4
(3)
6 5
The matrix A =
is the same matrix as in examples (16.3) and (16.4) above. In
1 2
this system the variables x and y are coupled. We will explain the logic of decoupling
later. In this example we will decouple the equations using some magical choices
involving eigenvectors.
Theexamples
above
showed that the eigenvalues of A are 7 and 1 and the eigenvectors
5
1
are
and
. We write our vectors in terms of the eigenvectors by making
1
−1
the change of variables
x
5
1
=u
+v
⇔ x = 5u + v; y = u − v.
y
1
−1
2
5
1
We also note that
=
−3
. Converting x and y to u and v we get
4
1
−1
6 5
x
6 5
5
1
5
1
=
u
+v
= 7u
+v
1 2
y
1 2
1
−1
1
−1
Thus
6 5
1 2
x
2
=
y
4
⇔
5
1
5
1
7u
+v
=
−3
1
−1
1
−1
It is easy to see that the last system is the same as the equations
v = −3.
7u = 1
In u, v coordinates the system is diagonal and easy to solve.
16.7 Introduction to matrix methods for solving systems of DE’s
In this section we will solve linear, homogeneous, constant coefficient systems
of differential equations using the matrix methods we have developed. For now
we will just consider matrices with real, distinct eigenvalues. In the next topic we
will look at complex and repeated eigenvalues.
7
16 Eigenvalues, diagonalization, decoupling
As with constant coefficient DE’s we will use the method of optimism to discover a
systematic technique for solving systems of DE’s. We start by giving the general 2 × 2
linear, homogeneous, constant coefficient system of DE’s. It has the form
x0 = ax + by
y 0 = cx + dy
where a, b, c, d are constants. There are a number of important things to note.
1. We can write equation (4) in matrix form
0 x
a b
x
=
⇔ x0 = Ax
y0
c d
y
a b
x
where A =
and x =
.
c d
y
(4)
(5)
2. The system is homogeneous. You can see this by taking equation (4) and putting
all the x and y on the left side so that the right side becomes all zeros.
3. The system is linear. You should be able to check directly that a linear combination
of solutions to equation (5) is also a solution.
We illustrate the method of optimism for solving equation (5) in an example.
Example 16.12. Solve the linear, homogeneous, constant coefficient system
x
6 5
0
x = Ax, where x =
and A =
.
y
1 2
answer: Using the method of optimism we try a solution
x = eλt v,
where λ is a constant and v is a constant vector. Substituting the trial solution into
both sides of the DE we get
λeλt v = eλt Av ⇔ Av = λv.
This is none other than the eigenvalue/eigenvector equation. So solving the system
amounts to finding eigenvalues and eigenvectors. From our previous examples we
know the eigenvalues and eigenvectors of A. We get two solutions.
1
t
7t 5
x1 = e
,
x2 = e
.
−1
1
The general solution is the span of these solutions:
1
t
7t 5
x = c1 x1 + c2 x2 = c1 e
+ c2 e
−1
1
8
16 Eigenvalues, diagonalization, decoupling
The solutions x1 and x2 are called modal solutions.
Now that we know where the method of optimism leads we can do a second example
starting directly with finding eigenvalues and eigenvectors
Example 16.13. Find the general solution to the system
0 x
3 4
x
=
0
y
1 3
y
and eigenvectors.
answer: First find eigenvalues
3 − λ
4 Characteristic equation: = 0 ⇔ λ2 − 6λ + 5 = 0 ⇒ λ = 1, 5.
1
3 − λ
Eigenvectors:
solve (A − λI)v = 0 2 4
2
λ = 1:
v = 0. Take v1 =
.
1
2
−1
−2 4
2
λ = 5:
v = 0. Take v2 =
.
1 −2
1
We have two modal solutions: x1 = eλt v1 and x2 = e5λt v2 .
2
λt
5λt 2
The general solution is x = c1 x1 + c2 x2 = c1 e
+ c2 e
.
−1
1
16.8 Decoupling systems of DE’s
Example 16.14. An uncoupled system
Consider the system
u0 (t) = 7u(t)
v 0 (t) = v(t)
Since u and v don’t have any effect on each other we say the u and v are uncoupled.
It’s easy to see the solution to this system is
u(t) = c1 e7t
v(t) = c2 et
In matrix form we have
0 u
7 0
u
=
.
v0
0 1
v
1
0
The coefficient matrix has eigenvalues are 7 and 1, with eigenvectors
and
.
1
0
The general solution to the system of DEs is
u
7t 1
t 0
= c1 e
+ c2 e
.
v
0
1
We see an uncoupled system has a diagonal coefficient matrix and the eigenvectors
are the standard basis vectors. All in all it’s simple and easy to work with.
9
16 Eigenvalues, diagonalization, decoupling
Example 16.15. Consider once again the system from example (16.7)
x0 = 6x + 5y
x
6 5
0
⇔ x = Ax, where x =
, A=
y 0 = x + 2y.
y
1 2
(6)
In this system the variables x and y are coupled.
5
From example (16.7) we know the eigenvalues are 7 and 1, the eigenvectors are
1
1
5
1
x
.
+ c2 et
and
, and the general solution is
= c1 e7t
−1
1
−1
y
Notice that c1 e7t and c2 et in the above solution are just u and v from the previous
example. So we can write
x(t)
5
1
= u(t)
+ v(t)
.
(7)
y(t)
1
−1
This is a change of variables. Notice that u and v are the coefficients in the
x
decomposition of
into eigenvectors. Also, since x and y depend on t so do u and
y
v.
Let’s rewrite the system (6) in terms of u, v. Using equation (7) we get
0
x
1
x
5
1
5
1
0 5
0
0
=u
x =
+v
and A
=A u
+v
= 7u
+v
y0
1
−1
y
1
−1
1
−1
The last equality follows because 5 1
T
T
and 1 −1 are eigenvectors of A.
Equating the two sides we get
1
5
1
0 5
0
u
+v
= 7u
+v
.
1
−1
1
−1
Comparing the coefficients of the eigenvectors we get
0 u0 = 7u
u
7 0
u
⇔
=
0
0
v = v
v
0 1
v
That is, in terms of u and v the system is uncoupled. Note that the eigenvalues of A
are precisely the diagonal entries of the uncoupled system.
Decoupling in general.
To end this section we’ll give a systematic method for decoupling a system.
Example 16.16. Decouple the system in example (16.7).
5 1
= matrix with eigenvectors of A as columns.
answer: Let S =
1 −1
7 0
Let Λ =
= diagonal matrix with the eigenvalues of A as diagonal entries.
0 1
10
16 Eigenvalues, diagonalization, decoupling
x
5
1
In the example we made a change of variable using
= u
+v
. In
1
−1
y
x
5 1
u
u
matrix form this is just
=
=S
y
1 −1
v
v.
u
−1 x
Inverting we have the change of variables
= S
. In example (16.8) we
v
y
found that this gives
0 u
7 0
u
u
=
=Λ
.
v0
0 1
v
v
Since u and v are uncoupled the change of variables u = S −1 x is called decoupling
16.8.1 Decoupling in general
Suppose we have the system x0 = Ax. If S is a matrix with the eigenvectors of A as
columns and Λ is the diagonal matrix with the corresponding eigenvalues as diagonal
entries. Then the change of variables u = S −1 x changes the coupled system x0 = Ax
into an uncoupled system u0 = Λu.
Proof. The key is diagonalization which is discussed in the next section. This says
that A = SΛS −1 . Thus, if x = Su we have
x0 = Ax
⇔
Su0 = ASu
⇔
Su0 = SΛS −1 Su = SΛu
⇔
u0 = Λu
16.9 Diagonalization
Decoupling by changing to coordinates based on eigenvectors can be organized into
what is called the diagonalization of a matrix. As usual we will see this first by
example.
6 5
Example 16.17. We know the matrix A =
has eigenvalues 7 and 1 with
1 2
T
T
corresponding eigenvectors v1 = 5 1 and v2 = 1 −1
We put the eigenvectors as the columns of a matrix S and the eigenvalues as the
entries of a diagonal matrix Λ.
5 1
7 0
S = v1 v2 =
,
Λ=
1 −1
0 1
The diagonalization theorem says that
5 1
7 0
1/6 1/6
−1
A = SΛS =
.
1 −1
0 1
1/6 −5/6
This is called the diagonalization of A. Note the form: a diagonal matrix Λ surrounded
by S and S −1 .
11
16 Eigenvalues, diagonalization, decoupling
Proof of the diagonalization theorem. We will do this for the matrix in the
example above. It will be clear that this proof carries over to any n × n matrix with n
independent eigenvectors. We could check directly that the diagonalization equation
holds. Instead we will give an argument based on matrix multiplication. Because the
eigenvectors form a basis superposition tells us that it will be enough to show that A
and SΛS −1 have the same effect on the eigenvectors v1 and v2 .
Recall that multiplying a matrix times a column vector results in a linear combination
of the columns. In our case
1
1
0
S
= v1 v2
= v1 , likewise S
= v2 .
0
0
1
Inverting we have
S
−1
1
v1 =
0
and
S
−1
0
v2 =
.
1
Now we can check that SΛS −1 v1 = Av1 and SΛS −1 v2 = Av2 :
1
7 0
1
7
−1
SΛS v1 = SΛ
=S
=S
= 7v1 = Av1
0
0 1
0
0
The last equality follows because v1 is an eigenvector of A with eigenvalue 7. The
equation of v2 is just the same. Since the two matrices have the same effect when
multiplied by a basis v1 , v2 of R2 they are the same matrix. QED
The example shows the general method for diagonalizing an n × n matrix A. The
steps are:
1. Find the eigenvalues λ1 , . . . , λn and corresponding eigenvectors
v1 , . . . , vn .
2. Make the matrix of eigenvectors S = v1 v2 · · · vn

λ1 0 0 · · · 0
 0 λ2 0 · · · 0 


3. Make the diagonal matrix of eigenvalues Λ =  ..

.. .. . .
.
. 0
. .
0 0 0 · · · λn
The diagonalization is: A = SΛS −1 .
Note: Diagonalization requires that A have a full complement of eigenvectors. If it
is defective it can’t be diagonalized.
We have the following important formula
det(A) = product of its eigenvalues.
This follows easily from the diagonalization formula
det(A) = det(SΛS −1 ) = det(S) det(Λ) det(S −1 ) = det(Λ) = product of diagonal entries.
12
16 Eigenvalues, diagonalization, decoupling
Example 16.18. Geometry of symmetric matrices. This is a fairly complex
a 0
example showing how we can use the diagonal matrix Λ =
and the rotation
0 b
cos θ − sin(θ)
matrix R =
to convert a circle to an ellipse as shown in the figures
sin(θ) cos(θ)
below.
To do this we think of matrix multiplication as a linear transformation. The diagonal
matrix Λ transforms the circle by scaling the x and y directions by a and b respectively.
This creates the ellipse in (b) which is oriented with the axes. The rotation matrix
R then rotates this ellipse to the general ellipse in (c).
v
Λj = bj
j
Λi = ai
u
i
(b) Ellipse made by scaling the axes by a and b
respectively
(a) Unit circle
y
−
v→
1 = RΛi
−
v→
2 = RΛj
θ
x
(c) Ellipse in (b) rotated by θ
In coordinates RΛ maps the unit circle u2 + v 2 = 1 to the ellipse shown in (c). That
13
16 Eigenvalues, diagonalization, decoupling
is,
u
x
RΛ
=
v
y
u
−1 −1 x
=Λ R
y
v
or
Example 16.19. Spectral theorem. The previous example transforms the unit
circle in uv-coordinates into an ellipse in xy-coordinates. In terms of inner products
and transposes this becomes
u
u
1=
,
v
v
−1 −1 x
−1 −1 x
,Λ R
= Λ R
y
y
T
x
x
=
(Λ−1 R−1 )T Λ−1 R−1
y
y
T
x
x
RΛ−2 R−1
=
y
y
The last equality uses the facts that for an orthogonal matrix RT = R−1 and for a
diagonal matrix ΛT = Λ.
Call the matrix occuring in the last two lines above
A = RΛ−2 R−1 = (Λ−1 R−1 )T Λ−1 R−1 .
We then have the equation of the ellipse is
T x
x
A
.
1=
y
y
The matrix A has the following properties
1. It is symmetric
2. Its eigenvalues are a−2 and b−2
→ and −
→ along the axes of the ellipse (see
3. Its eigenvectors are the the vectors −
v
v
1
2
figure (c) above).
4. Its eigenvectors are orthogonal.
Proof.
1. This is clear from the formula A = B T B where B = Λ−1 R−1 .
2. This is clear from the diagonalization A = RΛ−2 R−1 . (Remember the eigenvalues
are in the diagonal matrix Λ−2 .
→ to a multiple of itself. This also follows by
3. We need to show that A transforms −
v
1
considering the action of each term in the diagonalization in turn (see the figures):
→ to the x-axis; then Λ−2 scales the x-axis by a−2 ; and finally R rotates
R−1 moves −
v
1
→. Using symbols
the x-axis back the line along −
v
1
→ = RΛ−2 R−1 −
→ = RΛ−2 ai = R(a−2 ai) = a−2 −
→
A−
v
v
v
1
1
1
14
16 Eigenvalues, diagonalization, decoupling
The properties of A are general properties of symmetric matrices.
Spectral theorem. A symmetric matrix A has the following properties.
1. It has real eigenvalues.
2. Its eigenvectors are mutually orthogonal.
Because of the connection to the axes of ellipses this is also called the principal axis
theorem.
15