Download P,Q

Discrete
formal
logic
Mathematics
mathematical preliminaries
Chapter 3
Mathematical Reasoning
? Transparency
Transparency
No.No.
3-12-0
Discrete Mathematics Ch 3
Mathematical reasoning
Contents
1.5 and 3.1 Proofs ad proof methods
3.2 Mathematical Inductions
3.3 Recursive defined sets
Recursive definitions
Structural Induction
3.4 Recursive algorithms
3.5 Program correctness
Transparency No. 3-2
Discrete Mathematics Ch 3
Mathematical reasoning
Proofs and proof methods











Nature and importance of proofs
Applications of proofs
Proof terminology
Inference rules
Some inference rules
Soundness of inference rules
Formal proofs
Formal proof examples
Inference rules for quantifiers
common fallacies
proof methods
Transparency No. 3-3
Nature & Importance of Proofs
Discrete Mathematics Ch 3
Mathematical reasoning
 In mathematics, a proof is:
 a correct (well-reasoned, logically valid) and complete
(clear, detailed) argument that rigorously & undeniably
establishes the truth of a mathematical statement.
 Why must the argument be correct & complete?
 Correctness prevents us from fooling ourselves.
 Completeness allows anyone to verify the result.
 [Discrete] Mathematics requires a very high
standard for correctness and completeness of
proofs.
Transparency No. 3-4
Overview of §§1.5 & 3.1
Discrete Mathematics Ch 3
Mathematical reasoning
 Methods of mathematical argument (i.e., proof
methods) can be formalized in terms of rules of
logical inference.
 Mathematical proofs can themselves be
represented formally as discrete structures.
 Review both correct & fallacious inference rules,
& several proof methods.
Transparency No. 3-5
Applications of Proofs
Discrete Mathematics Ch 3
Mathematical reasoning
 Clear communication of logical arguments in any
area of study.
 Discovery and elucidation, through proofs, of
interesting new mathematical theorems.
 Theorem-proving has applications in program
verification, computer security, automated
reasoning systems, etc.
 Proving a theorem allows us to rely upon on its
correctness even in the most critical scenarios.
Transparency No. 3-6
Proof Terminology
Discrete Mathematics Ch 3
Mathematical reasoning
 Theorem [定理]
 A statement that has been proven to be true.
 Axioms[公設], postulates, hypotheses, premises
 Assumptions (often unproven) defining the structures
about which we are reasoning.
 Rules of inference [推論法則]
 Patterns of logically valid deductions from hypotheses
to conclusions.
Transparency No. 3-7
More Proof Terminology
Discrete Mathematics Ch 3
Mathematical reasoning
 Lemma[輔助定理] - A minor theorem used as a
stepping-stone to proving a major theorem.
 Corollary - A minor theorem proved as an easy
consequence of a major theorem.
 Conjecture - A statement whose truth value has
not been proven. (A conjecture may be widely
believed to be true, regardless.)
 Theory – The set of all theorems that can be
proven from a given set of axioms.
Transparency No. 3-8
Discrete Mathematics Ch 3
Mathematical reasoning
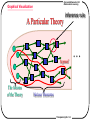
Graphical Visualization
A Particular Theory
inference rule
A proof
The Axioms
of the Theory
Various Theorems
Transparency No. 3-9
…
Inference Rules - General Form
Discrete Mathematics Ch 3
Mathematical reasoning
 Inference Rule –
 Pattern establishing that if we know that a set
of antecedent statements of certain forms are
all true, then a certain related consequent
statement is true.
 antecedent 1
antecedent 2 …
 consequent
“” means “therefore”
Transparency No. 3-10
Inference Rules & Implications
Discrete Mathematics Ch 3
Mathematical reasoning
 Each logical inference rule corresponds to
an implication that is a tautology.
 antecedent 1
Inference rule
antecedent 2 …
 consequent
 Corresponding tautology:
((ante. 1)  (ante. 2)  …)  consequent
Transparency No. 3-11
Some Inference Rules

p
 pq
Discrete Mathematics Ch 3
Mathematical reasoning
Rule of Addition
 pq
p
Rule of Simplification

Rule of Conjunction
p
q
 pq
Transparency No. 3-12
Discrete Mathematics Ch 3
Mathematical reasoning
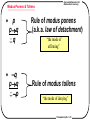
Modus Ponens & Tollens

p
pq
q
 q
pq
p
Rule of modus ponens
(a.k.a. law of detachment)
“the mode of
affirming”
Rule of modus tollens
“the mode of denying”
Transparency No. 3-13
Syllogism Inference Rules

pq
qr
pr
pq
p
q
Discrete Mathematics Ch 3
Mathematical reasoning
Rule of hypothetical
syllogism
Rule of disjunctive
syllogism
Aristotle
(ca. 384-322 B.C.)
Transparency No. 3-14
Formal Proofs
Discrete Mathematics Ch 3
Mathematical reasoning
 A formal proof of a conclusion C, given premises
p1, p2,…,pn consists of a sequence of steps, each
of which applies some inference rule to premises
or to previously-proven statements (as
antecedents) to yield a new true statement (the
consequent).
 A proof demonstrates that if the premises are
true, then the conclusion is true.
Transparency No. 3-15
Formal Proof Example
Discrete Mathematics Ch 3
Mathematical reasoning
 Suppose we have the following premises:
“It is not sunny and it is cold.”
“We will swim only if it is sunny.”
“If we do not swim, then we will canoe.”
“If we canoe, then we will be home early.”
 Given these premises, prove the theorem
“We will be home early” using inference
rules.
Transparency No. 3-16
Proof Example cont.
Discrete Mathematics Ch 3
Mathematical reasoning
 Let us adopt the following abbreviations:
 sunny = “It is sunny”; cold = “It is cold”;
swim = “We will swim”; canoe = “We will canoe”;
early = “We will be home early”.
 Then, the premises can be written as:
(1) sunny  cold
(2) swim  sunny
(3) swim  canoe
(4) canoe  early
Transparency No. 3-17
Proof Example cont.
Step
1. sunny  cold
2. sunny
3. swimsunny
4. swim
5. swimcanoe
6. canoe
7. canoeearly
8. early
Discrete Mathematics Ch 3
Mathematical reasoning
Proved by
Premise #1.
Simplification of 1.
Premise #2.
Modus tollens on 2,3.
Premise #3.
Modus ponens on 4,5.
Premise #4.
Modus ponens on 6,7.
Transparency No. 3-18
Discrete Mathematics
The formalization of proofs
and inference rules
? Transparency No. 2-0
What is a proof
Discrete Mathematics Ch 3
Mathematical reasoning
 what is a proof ?
 ==> a sequence of formulas (I.e., statements or
logical expressions)
 A1,
 ...
 An [=A]
generated according to some ( valid inference) rules
Transparency No. 3-20
Inference rules
Discrete Mathematics Ch 3
Mathematical reasoning
 An inference rule is a pattern of formulas of
the form:
 P1,P2,...,Pm (m  0) // C.
 Meaning that if P1,..,Pm have been produced
(proved, generated, etc) before then we can add C
to the proof sequence (now).
 P1,..,Pm : premises of the rule;
 C: Conclusion of the rule.
Transparency No. 3-21
Formal definition of proofs
Discrete Mathematics Ch 3
Mathematical reasoning
 Ax: a set of axioms
R: a set of inference rules
 A: a formula
 A proof of A (according to axioms Ax and rules R) is a
nonempty sequence of formulas A1,A2,...,An s.t.,
 1. An = A.
 2. For i = 1,.., n
 Either Ai is an axiom (i.e., a member of Ax) or
 there is an inference rule r: P1,..,Pm / C in R s.t.
1. C = Ai
2. {p1,..,Pm} {A1,...,Ai-1}
 Note:
 1. each Ai (i <n) is called a lemma.
 2. If B can be inferred from A directly, it is called a
corollary of theorem A.
 3. Both lemmas and corollaries are theorems.
Transparency No. 3-22
More about proofs
Discrete Mathematics Ch 3
Mathematical reasoning
 Notation: we use A1,A2,…Am |- C to means that
there is a proof of C with A1,…,Am as premises.
 An inference rule: P1,..,Pm // C is said to be
sound(可靠) (or correct[正確], valid[有效]) iff
 It is impossible that all premises are true
while the conclusion is false.
 I.e., If all premise are true than the conclusion
must be true.
 I.e., (P1/\P2/\…/\Pn ) C is a tautology.
 I.e., C is a logical consequence of P1,P2,… and
Pm.
Transparency No. 3-23
More about proofs
Discrete Mathematics Ch 3
Mathematical reasoning
 A fallacy is a inference rule which is not sound.
(I.e., It is possible that all premises are true but
the conclusion is false).
Ex: RainWet // ~Rain  ~Wet.
Fact1 : If P1,..,Pm // C is sound in T, and all premises
are theorems then so is the conclusion C.
Fact2: If
1. there is a proof of C from a set of premises P1,… Pn
(I.e., P1,…Pn |- C ),
2. all premises are theorems and
3. all inference rules used are sound, then
the conclusion C must be a theorem.
Transparency No. 3-24
Inference Rules for Quantifiers
Discrete Mathematics Ch 3
Mathematical reasoning
 x P(x)
P(o) (substitute any object o)
 P(o)
(substitute any extant object o)
x P(x)
Transparency No. 3-25
Example
Discrete Mathematics Ch 3
Mathematical reasoning
Topic #3 – Predicate Logic
 Definitions:
s :≡ Socrates (ancient Greek philosopher);
H(x) :≡ “x is human”;
M(x) :≡ “x is mortal”.
 Premises:
H(s)
Socrates is human.
x H(x)M(x)
All humans are mortal.
 Conclusion:
M(s)
Socrates is mortal.
Transparency No. 3-26
The proof
Discrete Mathematics Ch 3
Mathematical reasoning
Topic #3 – Predicate Logic
Some valid conclusions you can draw:
H(s)M(s)
[Instantiate universal.] If Socrates is human
then he is mortal.
H(s)  M(s)
Socrates is inhuman or mortal.
H(s)  (H(s)  M(s))
Socrates is human, and also either inhuman or mortal.
(H(s)  H(s))  (H(s)  M(s))
[Apply distributive law.]
F  (H(s)  M(s))
[Trivial contradiction.]
H(s)  M(s)
[Use identity law.]
M(s)
Socrates is mortal.
Transparency No. 3-27
Another Example
Discrete Mathematics Ch 3
Mathematical reasoning
Topic #3 – Predicate Logic
 Definitions: H(x) :≡ “x is human”;
M(x) :≡ “x is mortal”; G(x) :≡ “x is a god”
 Premises:
 x H(x)  M(x) (“Humans are mortal”) and
 x G(x)  M(x) (“Gods are immortal”).
 Show that x (H(x)  G(x))
(“No human is a god.”)
Transparency No. 3-28
The Derivation







Discrete Mathematics Ch 3
Mathematical reasoning
Topic #3 – Predicate Logic
x H(x)M(x) and x G(x)M(x).
x M(x)H(x) [Contrapositive.]
x [G(x)M(x)]  [M(x)H(x)]
x G(x)H(x)
[Transitivity of .]
x G(x)  H(x) [Definition of .]
x (G(x)  H(x)) [DeMorgan’s law.]
x G(x)  H(x)
[An equivalence law.]
Transparency No. 3-29
More Inference Rules for Quantifiers
 P(g)
 x P(x)
Discrete Mathematics Ch 3
Mathematical reasoning
(where g a general element of u.d.
I.e., g cannot be restricted to any
property except being an element
of u.d.)
 x P(x)
P(c) (substitute a new constant c
c is an object restricted to
property P)
Transparency No. 3-30
Example
Discrete Mathematics Ch 3
Mathematical reasoning
 The square of all odd numbers are odd.
pf: let g be any number.
[ if g is odd, then,
g = 2k + 1 for some k
g2 = 4kk + 4k + 1 = 2(2kk + 2k) + 1
=> g2 is odd. ]
=> Odd(g)  Odd(g2).
=> x Odd(x)  Odd(x2).
Transparency No. 3-31
Discrete Mathematics Ch 3
Mathematical reasoning
a fallacy
 Prove that x P(x) |- x P(x)
 What’s wrong with the proof: ?
 1.
 2.
 3.
x P(x)
P(c)
x P(x)
--- premise
--- instanciation
--- Gen
 Ans: c is not a general element!
Transparency No. 3-32
Discrete Mathematics Ch 3
Mathematical reasoning
Example inference rules
1. Modus Ponus(MP) : AB, A // B
2. abduction (ABD) : AB, B // A
3. denying premise : AB, ~A // ~B
4. Math. ind.: (let P be any formula )
P(0)
x P(x)  P(x +1)
-------------------------x P(x)
Notes:
1. rule 1 is correct.
2. rule 2,3 are in general not correct.
3. Rule 4 is correct for natural number(NT) theory, but not
correct for integer theory(ZT) and real number theory(RT).
Transparency No. 3-33
Some commonly used inference rules
Discrete Mathematics Ch 3
Mathematical reasoning
Rules of
inferences
Tautologies
Name
p // p\/q
p->(p\/q)
Addition
p/\q // p
p/\q->p
Simplication
p, p->q//q
p/\(p->q) -> q
Modus ponens
~q, p->q //~p
~q /\ (p->q) ->~p Modus Tollens
p->q,q->r//p->r
((p->q) /\ (q->r)) Hypothetical
-> (p->r)
syllogism
~p /\ (p \/q) -> q Disjunctive
syllogism
p\/q,~p //q
Transparency No. 3-34
Discrete Mathematics Ch 3
Mathematical reasoning
Some commonly used fallacies
 Affirming the conclusion [abduction]:
 From p->q, q infer p
 Ex: Do all exercises => learn discrete math.
Since have learned D.M., hence have done all exercises.
 note: p is a possible reason (explanation) of q, instead of a
(necessary) consequence of q.
 Denying the hypothesis:
 from ~p and p->q infer ~q.
 Ex: rain => wet, since not rain, hence not wet.
 Circular reasoning
 Assume n2 is even.
 n2 = 2k for some k.
 Hence n2 is even
Transparency No. 3-35
Techniques for proving theorems
Discrete Mathematics Ch 3
Mathematical reasoning
 Different ways of proving a theorem: p implies q.
 Vacuous proof: Prove that ~p. [~p //p->q]
 Trivial proof: Prove that q. [q // p->q ]
 Direct proof: Prove that if p then q. [p->q //p->q]
 suppose p, then ..., q
 Indirect proof: (proof by contraposition)
 Prove that "~q implies ~P" [~q->~p // p->q]
 Proof by contradiction:
 To prove P, it suffices to show that ~P -> F (false)
 [~p ->F // p]
 Proof by cases:
 To prove that "p \/ q implies r " it suffices to show that p->r
and q -> r.
 [p->r, q->r // (p\/ q) ->r.]
Transparency No. 3-36
Proof Methods for Implications
Discrete Mathematics Ch 3
Mathematical reasoning
For proving implications pq, we have:
 Direct proof: Assume p is true, and prove q.
 Indirect proof: Assume q, and prove p.
 Vacuous proof: Prove p by itself.
 Trivial proof: Prove q by itself.
 Proof by cases:
Show p(a  b), and (aq) and (bq).
Transparency No. 3-37
Direct Proof Example
Discrete Mathematics Ch 3
Mathematical reasoning
 Definition: An integer n is called odd iff
n=2k+1 for some integer k; n is even iff
n=2k for some k.
 Axiom: Every integer is either odd or even.
 Theorem: (For all numbers n) If n is an odd
integer, then n2 is an odd integer.
 Proof: If n is odd, then n = 2k+1 for some
integer k. Thus, n2 = (2k+1)2 = 4k2 + 4k + 1
= 2(2k2 + 2k) + 1. Therefore n2 is of the
form 2j + 1 (with j the integer 2k2 + 2k), thus
n2 is odd. □
Transparency No. 3-38
Indirect Proof Example
Discrete Mathematics Ch 3
Mathematical reasoning
 Theorem: (For all integers n)
If 3n+2 is odd, then n is odd.
 Proof: Suppose that the conclusion is false, i.e.,
that n is even.
Then n=2k for some integer k.
Then 3n+2 = 3(2k)+2 = 6k+2 = 2(3k+1).
Thus 3n+2 is even, because it equals 2j for
integer j = 3k+1.
So 3n+2 is not odd.
We have shown that ¬(n is odd)→¬(3n+2 is odd),
thus its contra-positive (3n+2 is odd) → (n is odd)
is also true. □
Transparency No. 3-39
Vacuous Proof Example
Discrete Mathematics Ch 3
Mathematical reasoning
 Theorem: (For all n) If n is both odd and even,
then n2 = n + n.
 Proof: The statement “n is both odd and even” is
necessarily false, since no number can be both
odd and even.
So, the theorem is vacuously true. □
Transparency No. 3-40
Trivial Proof Example
Discrete Mathematics Ch 3
Mathematical reasoning
 Theorem: (For integers n) If n is the sum of two
prime numbers, then either n is odd or n is even.
 Proof: Any integer n is either odd or even.
So the conclusion of the implication is true
regardless of the truth of the antecedent.
Thus the implication is true trivially. □
Transparency No. 3-41
Proving existence theorem
Discrete Mathematics Ch 3
Mathematical reasoning
Methods for proving x p(x):
 Constructive proof: find an object (or term) a, s.t.
P(a).
 [p(a) // x p(x) ]
 Nonconstructive proof: a proof of x P(x) w/o
knowing what object satisfies p.
 ex:proof by contradiction: Show that ~x p(x) ->F.
Transparency No. 3-42
Example of existence proofs
Discrete Mathematics Ch 3
Mathematical reasoning
Ex 20: [constructive proof] Show that there are n consecutive
composite integers for every integer n >0. (I.e. for all n x
(x+1,x+2,...x+n) are all composite.
Sol: Let x = (n+1)! +1.
=> x+i = (n+1)! + (i+1) = (i+1)( (n+1)!/(i+1) +1) is composite for
i = 1,..,n. QED.
Ex 21: [nonconstructive proof] For all n >0  prime number > n.
Sol: by contradiction. Assume n s.t. all prime number < n.
Let m = n! +1. ==> (k, m) = 1 for all k ≤ n.
=> all prime cannot divide m
=> m is a prime > n
=> a contradiction. QED.
Note: We cannot know a prime > n from the proof.
Transparency No. 3-43
Example of proof by cases...
Discrete Mathematics Ch 3
Mathematical reasoning
 Given n>0, prove there is a prime p>n.
 Consider x = n!+1. Since x>1, we know
(x is prime)(x is composite).
Case 1: x is prime. Obviously x>n, so let p=x and
we’re done.
Case 2: x has a prime factor p. But if pn, then p
mod x = 1. So p>n, and we’re done.
Transparency No. 3-44
Limits on Proofs
Discrete Mathematics Ch 3
Mathematical reasoning
 Some very simple statements of number theory
haven’t been proved or disproved!
 E.g. Goldbach’s conjecture: Every integer n≥2 is
exactly the average of some two primes.
 n≥2  primes p,q: n=(p+q)/2.
 There are true statements of number theory (or
any sufficiently powerful system) that can never
be proved (or disproved) (Gödel incompleteness
theorem).
Transparency No. 3-45
3.2 Mathematical Induction
Discrete Mathematics Ch 3
Mathematical reasoning
 To show that a property p hold for all nonnegative integer n,
it suffices to show that
1. Basis step: P(0) is true
2. Ind. step: P(n)  P(n+1) is true for all nonnegative
integer.
 P(n) in 2. is called the inductive hypothesis.
 Note: Math. Ind. is exactly the inference rule:
 P(0), n p(n)P(n+1) // n P(n) for any property P
 The second form of MI
 Basis: P(0) holds
 Ind. step: P(0) /\ P(1) /\ ...,/\p(n-1)  P(n) holds for all n.
 P(0) /\ P(1) /\ ...,/\p(n-1) (or for all k k<n => P(k)) is the ind.
hyp.
Transparency No. 3-46
Correctness of Math. Ind.
Discrete Mathematics Ch 3
Mathematical reasoning
 Correctness of MI.
Pf: Assume MI is incorrect. i.e. the set NP = {k | P(k) is false} is
not empty.
Let m be the least number of NP.
Since p(0), 0  NP and m >0.
=> m-1 exists and P(0),P(1),…,P(m-1) hold
 P(m) holds [by MI I or II]=> m  NP => a contradiction.
QED.
Transparency No. 3-47
Examples :
Discrete Mathematics Ch 3
Mathematical reasoning
2: Si=1,n 2i-1 = n2
3. n < 2n
4. 3 | n3 - n if n > 0
5.Si=1,n 2i = 2(n+1) -1
6. Sj=1,n arj = arn+1 - a / (r -1)
7. Let Hk = 1 + 1/2 +...+ 1/k => H2n  1 + n/2
8. |S| = n => |2S| = 2n.
9. 1 + 2+...+ n = n(n+1)/2
10. If n > 3 => 2n < n!
11. ~(S1 ...Sn) = ~S1 U ... U ~Sn.
Transparency No. 3-48
More examples:
Discrete Mathematics Ch 3
Mathematical reasoning
13: n >1 => n can be written as a product of primes.
[hint: use 2nd form of MI]
14. for every k >11, there are m,n s.t. k = 4m + 5n.
Transparency No. 3-49
Discrete Mathematics Ch 3
Mathematical reasoning
3.3 Recursive definitions
 Different ways of defining sets of objects
 Explicit listing
 Suitable for finite objects only.
 Define by giving an explicit expression
Ex: F(n) = 2n
 recursive (or inductive ) definition
Define value of objects (sequences, functions, sets, ...)
in terms of values of smaller similar ones.
Ex: the sequence 1,2,4,... (an = 2n) can be defined
recursively as follows:
1. a0 = 1;
2. an+1 = 2 x an for n > 0.
Transparency No. 3-50
Recursively defined functions
Discrete Mathematics Ch 3
Mathematical reasoning
 To define a function over natural numbers:
 specify the value of f at 0 (i.e., f(0))
 Given a rule for finding f(n) from f(n-1),..., f(0).
 i.e., f(n) = some expression in terms of n, f(n), ..., f(0).
 Ex1:
 f(n) = 3 if n = 0

= 2f(n-1) +3 if n >0
 => f(0) = 3,

f(1) = 2f(0) +3 = 9

f(2) = 2f(1)+3 = 21,...
 This guarantees f be defined for all numbers.
Transparency No. 3-51
Discrete Mathematics Ch 3
Mathematical reasoning
More examples functions
 Ex2: The factorial function f(n) = n!
 f(0) = 1
 f(n) = n f(n-1) for all n > 0.
 Recursively defined functions (over N) are well
defined
Pf: Let P(n) = "there is at least one value assigned to f(n)".
Q(n) = "there are at most one value assigned to f(n)".
We show P(n) hold for all n by MI..
basis: P(0) holds.
Ind. : assume p(k) holds for all k ≤ n
=> since f(n+1) can be assigned a value by evaluating the
expr(n,f(0),..,f(n)), where by ind. hyp. all f(i)s (i<n) have been assigned a
value.
The fact that Q(n) holds for all n is trivial, since each f(k) appear at the left
hand side of the definition exactly once. QED
Transparency No. 3-52
More examples:
Discrete Mathematics Ch 3
Mathematical reasoning
Ex5: The Fibonacci number:
 f(0) = 0; f(1) = 1;
 f(n) = f(n-1) + f(n-2) for n > 1.
 ==> 0,1,1,2,3,5,8,...
Ex6: Show that f(n) > a n-2 where a = (1+ sqrt(5))/2
whenever n ≥ 3.
Pf: (by MI). Let P(n) = "f(n) > a n-2 ".
Basis: P(3), P(4) holds. An easy check.
Ind.step: (for n >= 3)
If n ≥ 3 => an-1 = a2 an-3 = (a+1) an-3 = an-2 + a n-3.
If n ≥ 4 => by ind. hyp., f(n-1) >an-3, f(n) >an-2
Hence f(n+1) = f(n)+f(n-1) > a n-2 + a n-3 = a n-1. QED
Transparency No. 3-53
Lame's theorem
Discrete Mathematics Ch 3
Mathematical reasoning
 a,b: positive integer with a  b.
=> #divisions used by the Euclidean algorithm to find gcd(a,b) 
5 x #decimal digits in b.
Pf: seq of equations used for finding gcd(a,b)
where r0 = a, r1 = b.
r2 = ro mod r1  0
r3 = r1 mod r2  0
...
rn = rn-2 mod rn-1  0
rn+1 = rn-1 mod rn = 0
i.e., until rn | rn-1 and then gcd(a,b) = rn.
#division used = n. rn  1 = f2
rn-1  2rn  2f2 = f3; rn-2  rn+rn-1 = f2 + f3 = f4
...r2 r3 + r4 fn-1+fn-2=fn; b = r1 r2+r3fn+fn-1 = fn+1.> an-1.
logb > (n-1) log a ~ 0.208 (n-1) > (n-1)/5
n < 1 + 5 log b < 1 + 5 #digit(b). => n  5#digit(b).
Transparency No. 3-54
Recursively defined sets
Discrete Mathematics Ch 3
Mathematical reasoning
 Given a universal set U, a subset V of U and a set
of operations OP on U, we often define a subset D
of U as follows:
 1. Init: Every element of V is an element of D.
 2. Closure: For each operation f in OP, if f:Un->U and
t1,..,tn are objects already known to be in the set D, then
f(t1,..,tn) is also an object of D.
 Example: The set S = {3n | n >0} N can be defined
recursively as follows:
 1. Init: 3 ∈ S (i.e., V = { 3 } )
 2. closure: S is closed under +.
 i.e., If a,b ∈ S then so are a+b . (OP = {+})
Transparency No. 3-55
Notes about recursively defined sets
Discrete Mathematics Ch 3
Mathematical reasoning
1. The definition of D is not complete (in the sense that there
are multiple subsets of U satisfying both conditions.
Ex: the universe U satisfies (1) and (2), but it is not
Our intended D.
2. In fact the intended defined set
3': D is the least of all subsets of U satisfying 1 & 2, or
3'': D is the intersection of all subsets of U satisfying 1 & 2
or
3''': Only objects obtained by a finite number of applications
of rule 1 & 2 are elements of D.
3. It can be proven that 3',3'',and 3''' are equivalent.
4. Hence, to be complete, one of 3',3'' or 3''' should be
appended to condition 1 & 2, though it can always be
omitted(or replaced by the adv. inductively, recursively) with
such understanding in mind.
Transparency No. 3-56
Proof of the equivalence of 3',3'' and 3'''
Discrete Mathematics Ch 3
Mathematical reasoning
 D1: the set obtained by 1,2,3'
 D1 satisfies 1&2 and any S satisfies 1&2 is a superset of
D1.
 D2: the set obtained by 1,2,3''.
 D2 = the intersection of all subsets Sk of U satisfying 1&2.
 D3: the set obtained by 1,2,3'''.
 For any x ∈ U, x ∈ D3 iff there is a sequence
x1,...,xm = x, such that for each xi (i = 1.m) either
 (init: ) xi ∈ V or
 (closure:) there are f in OP and t1,...tn in {x1,..,xi-1} s.t.
 xi = f(t1,..,tn).
pf: 1. D2 satisfies 1&2 and is the least of all sets satisfying
1&2 , Hence D1 exists and equals to D2.
2.1 D3 satisfies 1 & 2.[ by ind.]
2.2 D3 is contained in all sets satisfying 1 & 2 [by ind.]
Hence D3 = D2.
Transparency No. 3-57
Example:
Discrete Mathematics Ch 3
Mathematical reasoning
 Ex 7': The set of natural numbers can be defined
inductively as follows:
 Init: 0 in N.
 closure: If x in N, then x' in N.
 => 0, 0',0'',0''',... are natural numbers

(unary representation of natural numbers)
Transparency No. 3-58
Induction principles III (structural induction)
Discrete Mathematics Ch 3
Mathematical reasoning
 D: a recursively defined set
 P; a property about objects of D.
 To show that P(t) holds for all t in D, it suffices to show that
 1. basis step: P(t) holds for all t in V.
 2. Ind. step: For each f in OP and t1,..,tn in D, if P(t1),...,P(tn)
holds, then P(f(t1,..,tn)) holds, too.
 Show the correctness of structural induction.
Pf: assume not correct. => NP = {t ∈ D | P(t) does not hold} is
not empty. => ∃ x ∈ NP s.t. ∃ a derivation x1,..xn of x and all
xi (i<n) ∉ NP.
=> If n =1, then x1 = x ∈ V (impossible)
Else either n > 1 and x ∈ V (impossible, like n=1)
or n > 1, and x=f(t1,.,tn) for some {t1,..,tn} in {x1,..xn-1}
and P holds for all tks => P(x) holds too => x ∉ NP, a
contradiction. QED.
Transparency No. 3-59
MI is a specialization of SI
Discrete Mathematics Ch 3
Mathematical reasoning
 Rephrase the SI to the domain N, we have:




To show P(t) holds for all t ∈ N, it suffices to show that
Init: P(0) holds
Ind. step: [OP={ ‘ }]
for any x in N, If P(x) holds than P(x') holds.
 Notes:
 1. The above is just MI.
 2. MI is only suitable for proving properties of natural
numbers; whereas SI is suitable for proving properties of
all recursively defined sets.
 3. The common variant of MI starting from a value c ≠ 0 ,1
is also a special case of SI with the domain
 D = {c, c+1, c + 2, … }
Transparency No. 3-60
well-formed arithmetic expressions
Discrete Mathematics Ch 3
Mathematical reasoning
Ex: (2 +x), (x + (y/3)),... (ok)
x2+, xy*/3 ... (no)
Let Vr = {x,y,..,} be the set of variables,
M = numerals = finite representations of numbers
OP = {+,-,x,/,^}
U = the set of all finite strings over Vr U M U OP U {(,)}.
The set of all well-formed arithmetic expressions (wfe) can be
defined inductively as follows:
1. Init: every variable x in Vr and every numeral n in M is a wfe.
2. closure: If A, B are wfe, then so are (x+y), (x-y), (x * y),
(x / y) and (x ^ y).
Note: "1 + x " is not a wfe. Why ?
Transparency No. 3-61
More examples:
Discrete Mathematics Ch 3
Mathematical reasoning
 Ex9: Wff (well-formed propositional formulas)






PV: {p1,p2,.. } a set of propositional symbols.
OP = {/\, \/, ~, -> }
U = the set of all finite strings over PV U OP U {(,)}
Init: every pi in PV is a wff
closure: If A and B are wffs, then so are
(A/\B), (A \/B), (A->B), ~A.
 Ex10: [strings]
 S: an alphabet
 S*: the set of finite strings over S is defined inductively
as follows:
1. Init: e is a string.
2. closure: If x is a string and a a symbol in S, then a·x is a
string.
Transparency No. 3-62
Discrete Mathematics Ch 3
Mathematical reasoning
 Ex11: Recursively define two functions on S*.






len : S* -> N s.t. len(x) = the length of the string x.
basis: i(e) = 0
Ind. step: for any x in S and a in S, len(ax) = len(x) + 1.
· : S* x S*  S* s.t. x · y = the concatenation of x and y.
Basis: e · y = y for all string y.
recursive step: (a · z) · y = a · (z · y) for all symbols a and
strings z,y.
 Prove properties of len(-) on S*:
Ex12: show that len(x · y) = len(x) +len(y) for any x,y ∈ S*.





By SI on x. Let P(x) = "len(xy) = len(x) +len(y)".
Basis: x = e. => x · y = y => len(x · y) = len(y) = len(e) + len(y).
Ind. step: x = az
len(x · y) = len((a · z) · y) = len((a · (z · y)) = 1 + len(zy)
= 1+ len(z) + len(y) =l(x) +l(y).
Transparency No. 3-63
Where we use Recursion
Discrete Mathematics Ch 3
Mathematical reasoning
 Define a domain
 numbers, lists, trees, formulas, strings,...
 Define functions on recursively defined domains
 Prove properties of functions or domains by
structural induction.
 compute recursive functions
 --> recursive algorithm
 Ex:
len(x){ // x : a string
if x = e then return(0)
else return(1+ l(tl(x))) }
Transparency No. 3-64
3.4 Recursive algorithm
Discrete Mathematics Ch 3
Mathematical reasoning
 Definition: an algorithm is recursive if it solve a
problem by reducing it to an instance of the same
problem with smaller inputs.
 Ex1: compute an where a ∈ R and n ∈ N.
 Ex2: gcd(a,b) a, b ∈ N, a > b
 gcd(a,b) =def if b = 0 then a
else gcd(b, a mod b).
 Ex: show that gcd(a,b) will always terminate.
 Comparison b/t recursion and iteration
 Recursion: easy to read, understand and devise.
 Iteration: use much less computation time.
 Result: programmer --> recursive program -->
 compiler --> iterative program --> machine.
Transparency No. 3-65
3.5 Program correctness
Discrete Mathematics Ch 3
Mathematical reasoning
 After designing a program to solve a problem, how can
we assure that the program always produce correct
output?
 Types of errors in a program:
 syntax error --> easy to detect by the help of compiler
 semantic error --> test or verify
 Program testing can only increase our confidence about
the correctness of a program; it can never guarantee that
the program passing test always produce correct output.
 A program is said to be correct if it produces the correct
output for every possible input.
 Correctness proof generally consists of two steps:
 Termination proof :
 Partial correctness: whenever the program terminates,
it will produce the correct output.
Transparency No. 3-66
Discrete Mathematics Ch 3
Mathematical reasoning
Program verification
 Problem:
 what does it mean that a program produce the
correct output (or results)?
By specifying assertions (or descriptions) about the
expected outcome of the program.
 Input to program verifications:
 Pr : the program to be verified.
 Q : final assertions (postconditions), giving
the properties that the output of the program
should have
 P : initial assertions(preconditions) , giving
the properties that the initial input values are
required to have.
Transparency No. 3-67
Hoare triple:
Discrete Mathematics Ch 3
Mathematical reasoning
 P,Q; assertions
 S: a program or program segment.
 P {S} Q is called a Hoare triple, meaning that
S is partially correct (p.c.) w.r.t P,Q,i.e., whenever P
is true for I/P value of S and terminates, then Q is
true for the O/P values of S.
Ex1: x=1 {y := 2; z := x+ y} z = 3 is true. Why ?
Ex 2: x = 1 { while x > 0 x++ } x = 0 is true. why?
Transparency No. 3-68
Discrete Mathematics Ch 3
Mathematical reasoning
Typical program constructs:
1. assignment: x := expr
 x := x+y-3
2. composition: S1;S2
 Execute S1 first, after termination, then execute S2.
3. Conditional:
 3.1 If <cond> then S
 3.2 If <cond> then S1 else S2.
4. Loop:
 4.1 while <cond> do S
 4.2 repeat S until <cond>
// 4.3 do S while <cond> …
 Other constructs possible, But it can be shown that
any program can be converted into an equivalent
one using only 1,2,3.1 and 4.1
Transparency No. 3-69
Assignment rule
Discrete Mathematics Ch 3
Mathematical reasoning
 P[x/expr] {x := expr } P
 P[x/expr] is the result of replacing every x in P by the
expression expr.
 ex: P = "y < x /\ x + z = 5" => P[x/3] = “y < 3 /\ 3+z = 5".
 Why correct?
 consider the variable spaces
 (...,x,...) == x := expr ==> (..., expr,...) |= P
 Hence if P[x/expr] holds before execution, P will hold after
execution.
 Example: Q {y := x+y} x > 2y + 1 => Q = ?
 (xb,yb) ==>{ya := xb+yb} ==>(xb,xb+yb) = (xa,ya) |= P(xa,ya) =def
‘’xa > 2ya +1’’
 => (xb,yb) |= Q = P(xa,ya)[xa/xb;ya/xb+yb]
 = P(xb,xb+yb)  “xb > 2(xb+yb) +1”
Transparency No. 3-70
Composition rules:
Discrete Mathematics Ch 3
Mathematical reasoning
 Splitting programs into subprograms and then show that
each subprogram is correct.
 The composition rule:
P {S1} Q
x = 0 { x:= x+2} ?
Q {S2} R
? { x := x-1} x > 0
--------------------------------------------------------P {S1;S2} R
x=0 {x:= x+2; x:= x -1} x > 0
 Meaning:
 Forward reading:
 Backward reading: to prove P{S1;S2}Q, it suffices to find
an assertion Q s.t. P{S1}Q and Q {S2}R.
 Problem: How to find Q ?
Transparency No. 3-71
Example:
Discrete Mathematics Ch 3
Mathematical reasoning
 Show that x =1 {y := 2; z := x +y} z = 3
 x = 1 {y := 2; z := x+y} z = 3
 ------------------------------------------------------- x=1 {y := 2} ?
? {z := x+y} z = 3
Transparency No. 3-72
Discrete Mathematics Ch 3
Mathematical reasoning
Classical rules
Classical rules:
P => P1
P1 {S} Q
---------------------P {S} Q
P {S} Q1
Q1 => Q
----------------------P{S} Q
P => P1
P1 {S} Q1
Q1 => Q
------------------------P {S} Q
Examples:
x = 1 => x+1>1
x+1>0 {x := x + 1} x > 0
x+1>1 { x := x + 1 } x > 1
x > 0 => x ≠ 0
----------------------------------- ----------------------------------x = 1 { x := x + 1} x > 1
x+1 > 0 {x := x+1 } x ≠ 0
Transparency No. 3-73
Conditional rules
Discrete Mathematics Ch 3
Mathematical reasoning
P /\ <cond> {S1} Q
P /\~ <cond> {S2} Q
-----------------------------------------------P {if <cond> then S1 else S2 } Q
T /\ x > y => x  x x x {y:=x} y  x
-----------------------------------------------P /\ <cond> {S} Q
T /\ x>y {y := x} y  x
P /\~<cond> => Q
~ x > y =>
yx
---------------------------------------------------------------P {if <cond> then S} Q
T {if x > y then y := x} y  x
Transparency No. 3-74
Discrete Mathematics Ch 3
Mathematical reasoning
While-loop rules
 Loop invariant:
 A statement P is said to be a loop invariant of a while
program: While <cond> do S, if it remains true after each
iteration of the loop body S.
 I.e., P /\ <cond> {S} P is true.
 While rule:
 P /\ <cond> {S} P
 ---------------------------------------------------- P {while <cond> do S} P /\ ~<cond>
 Issues:
 How to find loop invariant P?
 Most difficulty of program verification lies in the finding of
appropriate loop invariants.
Transparency No. 3-75
While loop example
Discrete Mathematics Ch 3
Mathematical reasoning
Show that
n>0 { i:= 1; f := 1;
while i < n do (i := i+1 ; f := f x i ) } f = n!
To prove the program terminates with f = n!, a loop invariant is
needed.
Let p = "i ≤ n /\ f = i!"
First show that p is a loop invariant of the while program
i.e., i  n /\ f = i! /\ i < n { i:= i+1; f:= f x i} i n /\ f=i!
Transparency No. 3-76
Discrete Mathematics Ch 3
Mathematical reasoning
while loop example(cont'd)
n > 0 ---
i:= 1;
------ i ≤ n
f := 1; ------ p = "i ≤ n /\ f = i! “
while i < n do (i := i+1 ; f := f x i )
------ p /\ ~ i < n ==> i=n /\ f = i!
==> f = n!
Transparency No. 3-77
Another example:
Discrete Mathematics Ch 3
Mathematical reasoning
Ex5:Show that the following program is correct:
Procedure prod(m,n: integer) : integer
1. If n < 0 then a := -n
else a := n ; ------ a = |n|
2. k := 0 ; x := 0
3. while k < a do
--- p = "x = mk /\ k ≤ a" is a loop
x := x + m;
invariant.
k := k+1
enddo
--- x = mk /\ k ≤ a /\ ~k<a => k=a /\ x=ma
=> x = m |n|
4. If n < 0 then prod := -x => prod = - m |n| = mn
else prod := x
=> Prod = m |n| = mn
---- prod = mn. Hence the program is [partially] correct !
Note: to be really correct, we need to show that the program
will eventually terminates.
Transparency No. 3-78