* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Frequency response I
Transmission line loudspeaker wikipedia , lookup
Stage monitor system wikipedia , lookup
Buck converter wikipedia , lookup
Alternating current wikipedia , lookup
Scattering parameters wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Loudspeaker wikipedia , lookup
Negative feedback wikipedia , lookup
Ringing artifacts wikipedia , lookup
Two-port network wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Chirp spectrum wikipedia , lookup
Opto-isolator wikipedia , lookup
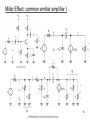
Utility frequency wikipedia , lookup
Zobel network wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Rectiverter wikipedia , lookup
RLC circuit wikipedia , lookup
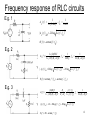
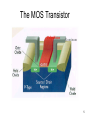
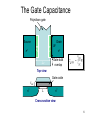
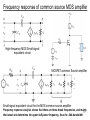
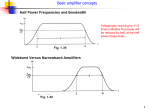
Frequency response I • As the frequency of the processed signals increases, the effects of parasitic capacitance in (BJT/MOS) transistors start to manifest • The gain of the amplifier circuits is frequency dependent, usually decrease with the frequency increase of the input signals • Computing by hand the exact frequency response of an amplifier circuits is a difficult and time-consuming task, therefore approximate techniques for obtaining the values of critical frequencies is desirable • The exact frequency response can be obtained from computer simulations (e.g SPICE). However, to optimize your circuit for maximum bandwidth and to keep it stable one needs analytical expressions of the circuit parameters or at least know which parameter affects the required specification and how 1 Frequency response II • The transfer function gives us the information about the behavior of a linear-time-invariant (LTI) circuit/system for a sinusoidal excitation with angular frequency T ( ) | T ( ) | exp( jT ( )) | T ( ) | exp( j ( )) • This transfer function is nothing but the ratio between the Fourier transforms of the output and input signals and it is also called the frequency response of the LTI circuit. • | T ( ) | represents the gain magnitude of the frequency response of the circuit, whereas ( ) is the phase of frequency response. Often, it is more convenient to express gain magnitude in decibels. • To amplify a signal without distortion, the amplifier gain magnitude must be the same for all of the frequency components 2 Frequency response of amplifers • • • A bode plot shows the the gain magnitude and phase in decibles versus frequency on logarithmic scale A few prerequisites for bode plot: Laplace transform and network transfer function Poles and zeros of transfer function Break frequencies Some useful rules for drawing high-order bode plots: Decompose transfer function into first order terms. Mark the break frequencies and represent them on the frequency axis the critical values for changes Make bode plot for each of the first order term For each first order term, keep the DC to the break frequency constant equal to the gain at DC After the break frequency, the gain magnitude starts to increase or decrease with a slope of 20db/decade if the term is in the numerator or denominator For phase plot, each first order term induces a 45 degrees of increase or decrease at the break frequency if the term is in the numerator or denominator Consider frequencies like one-tenth and ten times the break frequency and approximate the phase by 0 and 90 degrees if the frequency is with the numerator (or 0 and -90 degrees if in the denominator) 3 Add all the first order terms for magnitude and phase response Frequency response of RLC circuits E.g. 1 1 1 Av ( f ) , fb 1 j 2RCf 2RC | Av ( f )|db 20 log 1 ( f / f b ) 2 ( f ) arctan( f / f b ) E.g. 2 Av ( f ) 1 j 2fR2C 1 1 , f b1 , fb2 1 j 2f ( R1 R2 )C 2R2C 2 ( R1 R2 )C | Av ( f ) |db 20 log 1 ( f / f b1 ) 2 20 log 1 ( f / f b 2 ) 2 ( f ) arctan( f / f b1 ) arctan( f / f b 2 ) E.g. 3 Av ( f ) j( f / fb ) j 2fR2C R2 1 , fb 1 j 2f ( R1 R2 )C R1 R2 1 j ( f / f b ) 2 ( R1 R2 )C | Av ( f ) |db 12 20 log( f / f b ) 20 log 1 ( f / f b ) 2 ( f ) 90 arctan( f / f b ) 4 The MOS Transistor Polysilicon Aluminum 5 The Gate Capacitance Polysilicon gate Source Drain xd n+ xd Ld W n+ Gate-bulk overlap Top view Gate oxide tox n+ L n+ Cross section view 6 Gate Capacitance G G CGC CGC D S Cut-off G CGC D S Resistive D S Saturation Most important regions in digital design: saturation and cut-off 7 Diffusion Capacitance Channel-stop implant N A1 Side wall Source ND W Bottom xj Side wall LS Channel Substrate N A 8 Frequency response of common source MOS amplifer High-frequency MOS Small-signal equivalent circuit MOSFET common Source amplifier Small-signal equivalent circuit for the MOS common source amplifier Frequency response analysis shows that there are three break frequencies, and mainly 9 the lowest one determines the upper half-power frequency, thus the -3db bandwidth Exact frequency response of amplifiers • Exact frequency analysis of amplifier circuits is possible following the steps: Draw small-signal equivalent circuit (replace each component in the amplifier with its smallsignal circuit) Write equations using voltage and current laws Find the voltage gain as a ratio of polynomial of laplace variable s Factor numerator and denominator of the polynomial to determine break frequencies Draw bode plot to approximate the frequency response 10 The Miller Effect • Consider the situation that an impedance is connected between input and output of an amplifier The same current flows from (out) the top input terminal if an impedance Z in,Miller is connected across the input terminals The same current flows to (in) the top output terminal if an impedance Z out, Miller is connected across the output terminal This is know as Miller Effect Two important notes to apply Miller Effect: There should be a common terminal for input and output The gain in the Miller Effect is the gain after connecting feedback impedance Z f 11 Graphs from Prentice Hall Application of Miller Effect • If the voltage gain magnitude is large (say larger than 10) compared to unity, Z out, Miller Z f Av Av 1 Zf then we can perform an approximate analysis by assuming Z out, Miller is equal to Z f find the gain including loading effects of Z out,Miller ( z f ) use the gain to find out Z in,Miller Thus, using Miller Effect, gain calculation and frequency response characterization would be much simpler 12 Application of Miller Effect • If the feedback impedance is a capacitor C f ,then the Miller capacitance reflected across the input 1 terminal is Z . jC (1 A ) • Therefore, connecting a capacitance C f from the input to output is equivalent to connecting a capacitance C f (1 Av ) • Due to Miller effect, a small feedback capacitance appears across the input terminals as a much larger equivalent capacitance with a large gain (e.g. | Av | 80 ). At high frequencies, this large capacitance has a low impedance that tends to short out the input signal in, Miller f v 13 BJT small-signal models (for BJT amplifiers) The r model for low-frequency analysis The Hybrid model for high-frequency analysis rx The base-spreading resistance for the base region (very small) r VT / I CQ The dynamic resistance of the base emitter region r The feedback resistance from collector to base (very large) ro V A / I CQ Account for the upward slope of the output characteristic C The depletion capacitance of the collector-to-base region C The diffusion capacitance of the base-to-emitter junction Note: in the following analysis of the CE, EF and CB amplifier in the next three slides, we will assume rx 0, r for simplicity (though they still appear in the small signal models).14 Miller Effect: common emitter amplifier I 15 Miller Effect: common emitter amplifier II Assume the current flowing through C is very small compared to g m v , then ' the gain will be Avb ' g m RL considering the input terminal of the amplifier at b’ to ground. Applying the miller effect for the amplifier, the following simplified circuit can be obtained: C g m v Thus, the total capacitance from terminal b’ to ground is given as follows (neglect the miller capacitance from output terminal c to ground): CT C C (1 g m RL' ) Rs' Rs || R1 || R2 || r 1 fb 2Rs' CT The break frequency, thus the -3db frequency is set by the RC lowpass filter (other voltage controlled current source, resistance does not contribute to the 16 break frequency). C is a main limiting factor for -3db bandwidth. Emitter-follower amplifier • Using Miller Effect, we obtain the above equivalent circuit. If neglecting rx , r , It shows that the break frequency is fb 1 2 RT CT CT C C 1 g m RL' RT Rs' || [r (1 g m RL' )] Rs' Rs || RB RL' ro || RE || RL 17 Common base amplifier • What about amplifier that do not have capacitance connected directly from output to the input? For approximate analysis, we can neglect rx ( short circuit ), r , ro (open circuit ) the simplified equivalent circuit can be shown in (c). Derive the transfer function for this circuit, it shows two break frequencies (with typical values, f b1 is approximately -3db bandwidth) 1 1 ' ' f b1 , f , R R || R || r || ( 1 / g ), R Rc || RL 18 b 2 s s E m L 2 C Rs' 2 C RL'