Download 6-2 Equilibrium

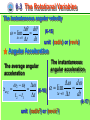
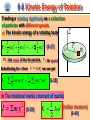
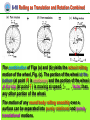
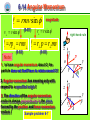
Bilingual Mechanics
Chapter 6
Rotation and
Angular Momentum
制作 张昆实 谢 丽
Yangtze University
Chapter 6 Rotation and Angular Momentum
6-1
6-2
6-3
6-4
6-5
What Is Physics?
Equilibrium
The Rotational Variables
Are Angular Quantities Vectors
Relating the Linear and Angular
Variables
6-6 Kinetic Energy of Rotation
Chapter 6 Rotation and Angular Momentum
6-7 Calculating the Rotational Inertia
6-8 Newton’s Second Law for Rotation
6-9 Work and Rotational Kinetic Energy
6-10 Rolling as Translation and Rotation
Combined
6-11 The Kinetic Energy of Rolling
6-12 The Forces of Rolling
Chapter 6 Rotation and Angular Momentum
6-13 Torque Revisited
6-14 Angular Momentum
6-15 Newton’s Second Law in Angular
Form
6-16 The Angular Momentum of a System
of Particles
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
6-18 Precession of a Gyroscope
6-1 What Is Physics
★ So far we have examined only the motion
of translation. In which an object moves
along a straight or curved line.
★ Now we deal with rotational motion of a
rigid body (a body with definite shape that
does’t change) about a fixed axis.
★ In this chapter we learn what is physics
through studying rotation of a regid body
and the related angular momentum.
6-2 Equilibrium
Consider these objects:
(1) a book resting on a table,
(2) a hockey puck sliding across a frictionless
surface with constant velocity,
(3) the rotating blades of a ceiling fan,
(4) the wheel of a bicycle that is traveling along a
straight path at constant speed.
Question
1 What is the linear momentum P and
the angular momentum L
of each of these four objects?
6-2 Equilibrium
• For each of these four objects:
1. The linear momentum P of its center of mass
is constant.
2. Its angular momentum L about its center of
mass, or about any other point, is also constant.
P  a constant , L  a constant
(6-1)
★ two requirements for equilibrium
objects satisfying Eq.(13-1) are said to be
in equilibrium.
6-2 Equilibrium
★ two requirements for equilibrium
P  a constant , L  a constant
(6-1)
● Static equilibrium
P0
L0
(constant =0)
objects in static equilibrium are not moving in any
way: either in translation or in rotation ( object (1))
● stable static equilibrium:
If a body returns to a state of
static equilibrium after having
been displaced from it.
● unstable static equilibrium:
If a small force can displace the
body and end the equilibrium.
6-2 Equilibrium
The analysis of static equilibrium is very
important in engineering practice.
Landing gear
6-2 Equilibrium
Static equilibrium in Building
designing is very important
especially in the earthquake
area !
6-2 Equilibrium
The Yangtze River bridge at JingZhou(荆州)
The analysis of static equilibrium
is also very important in designing
bridgies
6-2 Equilibrium
★ The
translational motion of a body
is governed by Newton's second
law in its linear momentum form :
dP
Fnet 
dt
(6-2)
If the body is in translational equilibrium
Fnet  0
(6-3)
P is a constant
dP dt  0
★ The
(balance of forces)
rotational motion of a body
is governed by Newton's second
law in its angular momentum form :
 net
If the body is in rotational equilibrium
 net  0
L is a constant
dL dt  0
dL

dt
(6-4)
(6-5)
(balance of torques)
6-2 Equilibrium
★ The
two Requirements for a body to be in Equilibrium
1. The vector sum of all the external forces that act on the
body must be zero.
Vector equation
Fnet  0
(balance of forces)
 Fnet , x  0

 Fnet , y  0

 Fnet , z  0
Component equations
(6-6)
2. The vector sum of all the external torques that act on the
body, measured about an possible point, must also be zero.
Vector equation
 net  0
(balance of torques)
 net , x  0

 net , y  0

 net , z  0
Component equations
(6-6)
6-2 Equilibrium
Consider the only simplifying situations: the forces only act on the
body lie in the xy plane. then the only torques that can act on the
body must tend to cause rotation around an axis parallel to the z axis.
With this assumption, we can eliminate one force equation and two
torque equations from Eqs. 6-6
 Fnet , x  0 √

 Fnet , y  0 √

 Fnet , z  0 ×
 net , x  0 ×

 net , y  0 ×

 net , z  0 √
(6-6)
★ Equilibrium
equations for a body lie in the xy plane:
(balance of forces)
(6-7)
Fnet , x  0
Fnet , y  0
 net , z  0
(balance of forces)
(6-8)
(balance of torques)
(6-9)
6-2 Equilibrium
The gravitational force on an
extended body is the vector sum
of the gravitational forces acting
on the individual elements of the
body.
cog
com
Fg
★ The gravitational force Fg on a body acts at
a specific point, called the center of gravity
(cog) of the body.
★ If g is the same for all elements of a body,
then the body’s center of gravity (cog) is
coincident with the body’s center of mass
(com).
xcog  xcom
6-3 The Rotational Variables
rigid body : a body that can rotate with all
its parts locked together and without any
change in its shape.
A rigid body is rotating about a fixed axis
In pure rotation, every point
of the body moves in a circle
whose center lies on the axis
of rotation, and every point
moves through the same
angle during a particular
time interval.
Rotation axis
Rigid
body
6-3 The Rotational Variables
★ Angular Position
A reference line (fixed in the body, perpendicular
to the rotation axis) is rotating with a rigid body.
The angular position of this
line is the angle of the line
relative to a fixed direction
(positive x axis, the zero
angular position )
s
  (radian measure)
r
1rev  360  2r r  2 rad
reference line
r

zero angular
position
(6-10)
(6-11)
1rad  57.3  0.159rev (6-12)
s
x
6-3 The Rotational Variables
★ Angular Displacement
  2  1
ω
(6-13)
An angular displacement in the
counterclockwise direction is
positive “+”, and one in the
clockwise direction is negative
“ ”
★ Angular Velocity
average angular velocity
avg
z
 2  1



t 2  t1
t
r
t2
.
1  . t1
O
x
z

z


(6-14)
0
0
6-3 The Rotational Variables
The instantaneous angular velocity
 d
  lim

t 0 t
dt
(6-15)
unit (rad/s) or (rev/s)
★ Angular Acceleration
The average angular
acceleration
 avg 
2  1
t2  t1


t
(6-16)
The instantaneous
angular acceleration
 d
  lim

t  0 t
dt
unit (rad/s2) or (rev/s2)
(6-17)
6-4 Are Angular Quantities Vectors
Can we treat the angular displacement, velocity,
And acceleration of a rotating body as vectors?
For angular velocity, there are only two directions.
★ Right hand rule
Curl you right hand about
rotating disk, your fingers
pointing in the direction of
rotation. Your extended thumb
points in the direction of the
angular velocity vector.
z

In pure rotation, a vector defines an axis of rotation,
not a direction in which something moves !
6-4 Are Angular Quantities Vectors
caution
Angular displacements
(unless they are very small)
cannot be treated as vectors!
A vector must obey the rules
of vector addtion, one of
which says that if you add
two vectors, the order in
which you add them does not
matter.
Angular displacements fail
this test !
6-4 Are Angular Quantities Vectors
In pure rotation, the case of constant angular
acceleration is very important !
Equations of Motion for Constant Linear Acceleration and for Constant Angular Acceleration
Equation
Number
(2-43)
(2-47)
(2-48)
v  v0  at
Linear
Equation
v  v0  at
x  x0  v0t  12 at 2
Angular
Equation
  0  t
   0  0t  12  t 2
2
2



 2 (   0 )
0
v  v  2a ( x  x0 )
2
2
0
(2-49)
x  x0  12 (v0  v)t
(2-50)
x  x0  vt  12 at 2
Three replacements:
Equation
Number
(6-18)
(6-19)
(6-20)
  0  12 (0   )t (6-21)
   0  t  12  t 2 (5-22)
x   , v  , a  
6-5 Relating the Linear and Angular Variables
Relate the linear variables s, v and
to the angular variables  ,  and 
★ The Position
s  r (radian measure) (6-23)
v
a
M
at
s
ar
a


r
★ The Speed
M0
Differentiating Eq6-23 with respect to t
d
ds d ds
is the linear speed,

r
dt
dt dt
dt
So we can obtain :
v  r

is the angular speed
(radian measure) (6-24)
Caution: The angle
and the angular speed
measured in radians.

must be
6-5 Relating the Linear and Angular Variables
The period of revolution T for the motion of each point
and for the rigid body itself is
2 r
T 
v


(6-25)
Substituting for v from Eq.6-24
and canceling r, we can find
2
T 
(radian measure) (6-26)

et
ar 
r


 v
at

★ The Acceleration
Tangential acceleration
differentiating
v  r
dv d 
(6-27)
at 

r  r
(6-28)
dt
dt
radial acceleration
v 2 ( r )2
ar 

  2 r (6-29)
r
r
(radian measure)
6-6 Kinetic Energy of Rotation
Treating a rotating rigid body as a collection
of particles with different speeds.
★ The kinetic energy of a rotating body
1 2 1
1 2
2
K  m1v1  m2 v2  ....   mi vi (6-37)
2
2
2
O
z
ri m
i
mi : the mass of the ith particle, vi: Its speed
Substituting for v from v  r, we can get
1
1
2
K   mi ( ri )  ( mi ri 2 ) 2
2
2
(6-38)
★ The rotational inertia ( moment of inertia)
I  mi ri
2
(6-39)
1
K  I 2
2
(radian measure)
(6-40)
6-6 Kinetic Energy of Rotation
★ The rotational inertia ( moment of inertia)
I  mi ri
2
(6-39)
The SI unit for I is kilogram-square
meter ( kg  m 2 )
★ The rotational inertia of a rigid body depends on:
(1) the mass of the rigid body ;
(2) the mass distribution;
(3) the rotation axis
(a) Parallel-Axis Theorem
(b) Perpendicular-Axis Theorem
6-7 Calculating the Rotational Inertia
If a rigid body consists of a great many adjacent par2
ticles, replace the sum in I   mi ri with an integral:
I   r dm
2
( rotational inertia,
continuous body )
(6-41)
Example:
There is a uniform circular disk
with mass m and radius R ,
what is the rotational inertia of
the disk about the axis through
the center o , perpendicular to
the disk?
( 漆安慎力学：P223 例题1 )
m
h
 o
R
6-7 Calculating the Rotational Inertia
Solution: The key idea here is that we divide the
disk into infinite number of thin rings, the mass
of the ring at radius r with width dr is
dm    2 rhdr ( h: thickness ,  : density)
then the rotational inertia of the ring
can be found dI  r 2 dm  2 hr 3dr
Through integration we get
R
I   r dm  
0
2
R
0
1
4
2 hr dr   hR
2
3
h
m
 oo
r
dr
Since m   h R 2, the rotational
inertia of the disk is
1
I  mR 2
2
R
mass element
6-7 Calculating the Rotational Inertia
TABLE 6-2 Some Rotational Inertias
6-7 Calculating the Rotational Inertia
★ Parallel-Axis Theorem
As show in the figure, an axis zc goes through
the center of mass of a rigid body, the rotational
inertia of the body about this axis is Icom . If
another axis z paralle to zc, it can be proved that
the rotational inertia of the rigid body about the z
axis is
I  I com  Mh
2
z
Zc
(6-42)
(parallel-axis theorem)
Where M is the mass of the rigid
body, h is the distance between
the two parallel axes.
M
h
C
6-7 Calculating the Rotational Inertia
★ Proof of the Parallel-Axis Theorem
Let O be the center of mass of the arbitrary shaped
body. Consider an axis through O perpendicular to the
plane, and another axis through point P parallel to the
first axis.
Let dm be a mass element with the general coordinate
x and y. The rotational inertia of the body about the axis
through P is
I   r 2 dm   [( x  a )2  ( y  b )2 ]dm
axis
y Rotation
through P
r
I   ( x  y )2 dm  2a  xdm  2b  ydm   ( a  b )2 dm
0
R2
0
I   R dm   h dm  I com  Mh
2
2
h2
2
dm
y- b
p • x-a
h b
o
a
Rotation axis through
center of mass
x
6-7 Calculating the Rotational Inertia
Sample Problem 6-3
A thin, uniform rod of mass M and length L lies on
an x axis with the origin at the rod’s center.
(a) What is the rotational inertia of the rod about the
perpendicular rotation axis through the center?
(b) What is the rod’s rotational inertia I about a new
rotation axis that is perpendicular to the rod and
through the left end?
M
com
L
2
L
2
(a)
x
M
L
(b )
x
6-7 Calculating the Rotational Inertia
Solution: (a) for a continuous
object using
I  r 2 dm
dm

mass element
dm  ML dx
I com  
L2
L 2
M
rx
x ( )dx 
2 M
L
1
12
L
0
1
3
L
2
M
x
L
2
dm
2
1
3
I   x ( )dx  ML
2 M
L
x
ML
I  ML  M ( )  ML
L 2
2
dx
(a)
2
I  I com  Mh
2
com
L
2
Solution: (b) using parallel-axis
theorem
2
1
12
x
2
x
M
dx
x
L
(b )
6-7 Calculating the Rotational Inertia
★ Perpendicular-Axis Theorem ( 漆安慎力学：P225 )
The rigid body is a very thin plate, a coordinate system
is chosen as the figure shows with the x and y axes lie
in the plate and the z axis perpendicular to the plate.
The rotational inertia of the rigid body about the z axis is
I z  mi ri
2
z
I z  mi x  mi y
2
i
Iz  Ix 
2
i
(perpendicularI y axis theorem)
Where I x , I y is the rotational inertia
about the x, y axis, respectively.
xi
x
o
ri
yi
mi
y
6-7 Calculating the Rotational Inertia
z
★ Perpendicular-Axis Theorem
Iz  Ix  I y
m
(perpendicular-axis theorem)
x
Example: What is the rotational inertia
of a disk about any diameter?
x , y axes are lie in the plane of the
disk,
y
z
m
z axis is perpendicular to them.
C
R
I z  I x  I y  2I x
I z  mR
(from symmetry)
I x  I y  I z  mR
1
2
2
1
2
x
1
4
2
y
6-7 Calculating the Rotational Inertia
★ Torque
A force F is applied on a body (only shown a cross
section)

F
Ft
radial component FF
rr
tangential component
torque

F

Ft
  (r )( F sin  )
F
Rotation
axis
o


F
 Line
of
r
r
r
action of F

Moment arm of F
Two equivalent ways of computing the torque
  ( r )( F sin  )  rFt
  ( r sin  )( F )  r F

r : the moment arm
6-7 Calculating the Rotational Inertia
torque
  (r )( F sin  )
  ( r )( F sin  )  rFt
  ( r sin  )( F )  Frr F

Ft

F
Rotation
axis
o

F


F
 Line
of
r
r
r

action of F
The ability of F to rotate the body
Moment arm of F
depends not only on the magnitude
of its tangential component Ft , but
SI unit : N• m
also on just how far from o the force
is applied.
Torques obey the superposition principle : when several
torques act on a body, the net torque (or resultant torque)
is the sum of individual torques.
net


torque: counterclockwise positive; clockwise negative
6-8 Newton’s Second Law for Rotation
★ Newton’s
Second low for rotation
Fnet  ma
 net  I
Fnet   net , m  I ,
y
F
(6-45)
Ft
a 

Fr
m
r
A force act on the particle ,only the
Rod
tangential component Ft of the force

can accelerate the particle along the o Rotation axis
circular path. So with the Newton’s
second law we can write
From
x
at   r
Ft  mat
The torque acting on the particle is
  Ft r  mat r
  m( r )r  ( mr )
2
  I
 net  I 
(6-47)
( radian
measure )
(6-48)
6-9 Work and Rotational Kinetic Energy
with the work- kinetic energy theorem (Eq 4-10) ,we relate
the change  K in kinetic energy to the work W, writing
★
1 2 1 2
K  K f  Ki  mv f  mvi  W
2
2
W 
xf
xi
Fdx
(work, one-dimensional)
(6-52)
(6-53)
The rate at which the work is done is the power, which
we can find with Eqs 4-41 and 4-46
dW
P
 Fv
dt
(power, one-dimensional) (6-54)
6-9 Work and Rotational Kinetic Energy
★A
rotational situation is similar, so we can write
a rotational kinetic energy as
1 2 1 2
K  K f  Ki  I  f  I  i  W (work-kinetic energy theorem) (6-55)
2
2
We can calculate the work with a rotational equivalent of Eq6-53
W 
f

 d
(work, rotation about fixed axis)
(6-56)
i
 is constant, Eq 6-56 reduces to
W   ( f  i ) (work, constant torque)
When
(6-57)
The rate at which the work is done is the power
dW
P
 
dt
(power, rotation about fixed axis)
(6-58)
6-9 Work and Rotational Kinetic Energy
★
Proof of Equation 6-55 through 6-58
During the rotation, force F does work on the body. Let’s assume
that the only energy of the body that changed by F is the kinetic
energy. Then we can apply the work-kinetic energy theorem
K  K f  K i  W
Using k  12 mv 2 and
K 
Substituting
v  r
(6-59)
we can rewrite the Eq6-59
1 2 2 1 2 2
mr  f  mr  i  W
2
2
I  mr
2
(6-60)
into Eq 6-60 yields
1
1
2
K  I  f  I  2i  W
2
2
6-9 Work and Rotational Kinetic Energy
We write that work dW as Ft ds. However, we can replace ds with
Thus we have
dW  Ft rd 
From
d .
(6-61)
  Ft r ，we can rewrite Eq 6-61 as
dW  d 
(6-62)
The work done during a finite angular
displacement from i to f is then
We can find power P for rotational
motion from Eq 6-62
W 
f

 d
i
dW
d
P

 
dt
dt
6-9 Work and Rotational Kinetic Energy
6-3
From Left to Right : Five replacements
x   , v  , a   , m  I , F  
6-10 Rolling as Translation and Rotation Combined
Consider only objects that roll smoothly along
a surface without slipping.
Rolling can be treated as a combination of the
translation of the center of mass and rotation
of the rest of the object around that center.
6-10 Rolling as Translation and Rotation Combined
A bicycle wheel rolls along a street. During a time interval
t , both O and the contact point P move a distance s . The
wheel rotates through an angle  about the center of the
wheel, The initial contact point
P moves through arc length s :
s R
(6-66)
R
Differentiating Eq. 6-66
with respect to time (with R
held constant) gives us
vcom   R
(6-67)
(smooth rolling motion)
P
6-12
P
6-10 Rolling as Translation and Rotation Combined
+
=
T
P
The combination of Figs (a) and (b) yields the actual rolling
motion of the wheel, Fig. (c). The portion of the wheel at the
bottom (at point P) is stationary and the portion of the wheel
at the top (at point T ) is moving at speed 2vcom , faster than
any other portion of the wheel.
The motion of any round body rolling smoothly over a
surface can be separated into purely rotational and purely
translational motions.
6-10 Rolling as Translation and Rotation Combined
★ Rolling as Pure Rotation： Another
way to look at the rolling motion of the wheel

We consider the rolling motion to be pure
rotation about an axis passing through
point P in Fig 6-22c and perpendicular to
the plane of the figure. The vectors in
Fig.6-24 then represent the instantaneous
velocities of points on the rolling wheel.

P
6-24
What is the angular speed of the rolling
wheel about the new axis ?

The same angular speed
as that the
wheel rotates about its “ COM ” axis !
vtop  (  )( 2 R )  2( R )  2Vcom
vcom  (  )( R )  R v p  (  )( 0 )  0
6-22
Check this answer by calculating
the lineal speed at the top point T,
and the point O and P
We get the same results !
6-11 The Kinetic Energy of Rolling
If we view the rolling as pure rotation about an
axis through P in Fig. 6-24, then from Eq. 6-40
1
K  I 2
2
1
2
K  I P
2
(6-68)
where  is the angular speed of the wheel and I P
is the rotational inertia of the wheel about the axis
through P. From the parallel-axis theorem, we have
I P  I com  MR
2
(6-69)
where M is the mass of the wheel, I com is its rotational
inertia about an axis through its center of mass.
6-11 The Kinetic Energy of Rolling
1
K 
I P 2
2
I P  I com  MR
2
1
1
2
2 2
K  I com  MR 
2
2
vcom   R ， yields
1
1
2
2
K  I com  Mvcom Konig’s
theorem
2
2
Using the relation
(6-70)
A rolling object has two type of kinetic energy :
2
1
a rotational kinetic energy ( 2 I com ) due to its
rotation about its center of mass and a translational kinetic energy ( 1 Mv 2 ) due to translation
com
2
of its center of mass.
6-12 The Forces of Rolling
★ Friction and Rolling
If a net force acts on the rolling wheel to
speed it up
cause acom and
.

tend to make the wheel slide at P.

Tendency
of slide
fs
A frictional force must acts on the wheel
at P to oppose that sliding tendency.
If the wheel does not slide, that frictional
force is a static frictional force f , the
s
motion is smooth rolling.
Differentiating vcom   R with respect to time we have
acom   R
(smooth rolling motion) (6-71)
6-12 The Forces of Rolling
★
Rolling down a Ramp
A round uniform body of radius R rolls
smoothly down a ramp at angle
, along
an
axis.

x
N
Fg sin 
R
★ The gravitational force
Fg , acting at the
COM of the body. Its component along the
ramp is Mg sin 
★ A normal force


Fg
fs
P
Fg cos 
, acting at point P but
is shifted to the COM of the body.
N
★ A static frictional force
f s , acting at point
P and is directed up the ramp.
We can write Newton’s second law for components along the x axis
as
Fnet , x  max
f s  Mg sin   Macom, x
(6-72)
x
6-12 The Forces of Rolling
★ Rolling down a Ramp
N
Next, check all the external torques
acting on the rolling body :
Fg sin 
R
★ the torque of the frictional force :
 Rf s
( counterclockwise )
★ the torque of the gravitational
force :
F (0) ( zero moment arm )


Fg
fs
x
P
Fg cos 
g
★ the torque of the normal force :
N (0)
( zero moment arm )
Apply Newton’s second law in
angular form to the body’s rotation
about its center of mass.
 net  I
Rf s  I com
(6-73)
6-12 The Forces of Rolling
Because the body is rolling smoothly, we can use Eq.6-71 (acom  R )
but we must be cautious because here
is negative ( in the
com
negative direction of x axis ) and
is positive (counterclockwise).
Thus substitute a
/ R for


com
Then, solving for
f s   I com
fs
, we obtain
acom , x
R2
a
(6-74)
f s  Mg sin   Macom, x
Substituting the right side of Eq. 6-74 for
acom, x
fs
in Eq. 6-72, we then find
g sin 

1  I com / MR 2
(6-75)
We can use this equation to find the linear acceleration
any body rolling along an incline of angle
(6-72)

acom , x of
with horizontal.
6-13 Torque Revisited

Torque 
Torque
fixed axis; counterclockwise : +

; clockwise:

fixed point; may have any direction! (expanded defination)
A , r is its position
A single force F acts on the
A particle is at point
vector.
particle.
z 

★ The torque
acts on the particle
relative to the fixed point O is a vector
quantity defined as
  rF

z


F
F
o r
O 

r

*
A
P
(6-76)
We use the right-hand rule for vector products, sweeping
the fingers of the right hand from r (the first vector in the
product) into F (the second vector). The outstretched right
thumb then gives the direction of  .
6-13 Torque Revisited
Determine the magnitude of a torque 
  rF
( Torque defined )
  rF sin 
F  F sin 
(6-77)
r  r sin 
  rF   r F
(6-78)
:
z 

o
F
r

r

F
F

A
(6-79)
r Moment arm of F
6-14 Angular Momentum
A particle of mass m passes through point A with linear momentum
p( mv ), r
is the position vector of the particle.
right-hand-rule
The angular momentum of the particle with
respect to the origin O is a vector quantity
 r  P  m(r  v)
z
(6-80)
p
o
The SI unit of
is (kg.m2/s) or (J. s)
x
 rmv sin 
r
A
Using the right-hand rule we can determine
the direction of the angular momentum .
x
(6-81)

p
z
o
The magnitude of
p
y
y
r
r 
A
p
6-14 Angular Momentum
 rmv sin 
v  v sin 
(6-81)
 rp  rmv
(6-82)
magnitude
r  r sin 
right-hand-rule
 r p  r mv
z
(6-83)
Note:
1. to have angular momentum about O, the
particle does not Itself have to rotate around O !
p
o
x
p
r
A
2. Angular momentum has meaning only with
respect to a specified origin !
3. The direction of the angular momentum
vector is always perpendicular to the plane
formed by the position and linear momentum
vectors !
Sample problem 6-7

y
p
z
o
x
y
r
r 
A
p
6-15 Newton’s Second Law in Angular Form
Newton’s second law written in the form
F net
dP

dt
(single particle)
(6-84)
We have seen enough of the parallelism between linear and
angular quantities. Guided by Eq.6-84, we guess the relation
between torque and angular momentum must be
 net
d

dt
(single particle)
(6-85)
★ The (vector) sum of all the torques acting on a particle is equal to
the time rate of change of the angular momentum of that particle.

Note: defined with the
same origin !
The torques
and the angular momentum
must be
6-15 Newton’s Second Law in Angular Form
Prove of Eq.6-85
 net 
We know the definition of the
angular momentum of a particle:
d
dt
 m(r  v)
Differentiating each side with respect to time t yields
d
dv dr
 m( r 

 v)
dt
dt
dt
d
 m( r  a  v  v )
dt
v v  0
(6-86)
d
 m( r  a )
dt
ma  Fnet
We now use Newton’s Second law, obtaining
(6-87)
d
 r  F net  (r  F )
dt
 net
d

dt
(6-85)
6-16 The Angular Momentum of a System of Particles
The total angular momentum L of a system of particles is
the (vector) sum of the angular momenta
of the individual
particles:
n
L
1

2

3
 .... 
n

i
(6-88)
i 1
By taking the time derivative of Eq.6-88. The change in
be found
(6-89)
dL

dt
n
d

i 1 dt
dL

dt
L can
n

net ,i
(6-90)
i 1
The only torques that can change the total angular momentum L of the system are the external torques acting on
the system.
The sum of the internal torques due to the interaction
between the particles is zero !
6-16 The Angular Momentum of a System of Particles

Let net represent the net external torque. Then Eq.6-90
becomes
dL (system of particles) (6-91)
 
net
dt
This is the Newton’s second law in angular form.
The net extenal torque  net acting on a system of particles
is equal to the time rate of change of the system’s total
angular momentum L .
caution
1. Torques and system’s angular momentum
must be measured relative to the same origin.
2. If the center of mass of the system is not accelerating
relative to an inertia frame, that origin can be any point ;
if the center of mass of the system is accelerating, the
origin can be only at that center of mass .
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
A rigid body rotates about the z axis with angular speed  .
a mass element of mass mi within the body is located by
the position vector ri . It moves about the z axis in a circle
with radius r i and has the linear momentum pi .
ri
The magnitude of the angular momentum
of this mass element, with respect to O is
pi
i
ri
iz
i
i
 ( ri )( pi )(sin 900 )  ( ri )( mi vi )
The angular momentum vector
for the
i
mass element is Shown in Fig.b; its direction
must be perpendicular to those of ri and pi .
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
The
iz
z
cmponent of
i
is
 i sin   (ri sin  )(mi vi )  ri mi vi
Because
v   r , we may write
n
LZ  
i 1
n
iz
n
n
  mi vi ri   mi (ri )ri   ( mi r2i )
i 1
i 1
i 1
n
The quantity
(6-92)
2 is the rotational inertia

m
r
I of the
 i i
i 1
body about the fixed Axis .Thus Eq. 6-92 reduces to
Lz  Iz
z
( rigid body, fixed axis )
(6-93)
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
6-4
6-3
From Left to Right : six replacements
x   , v  , a   , m  I , F   ,
p
PL
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
six repla-
6-3
cements
x ,
v  ,
a  ,
m  I,
6-4
F ,
p
6-3
PL
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
The law of conservation of angular momentum
If no net external torque
acts on the system
or
 net  dL dt
L = a constant
net angular momentum
at some initial time
i
t
Li  L f
dL dt  0
( isolated system ) (6-94)
=
net angular momentum
at some later time
f
( isolated system )
t
(6-95)
★ The law of conservation of angular momentum
If the net external torque acting on a system
is zero, the angular momentum L of the system
remains constant, no matter what changes take
place within the system.
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
The law of conservation of angular momentum
L
= a constant
or
Li  L f
( isolated system ) (6-94) (6-95)
★ If the component of the net external torque on a
system along a certain axis (  z ) is zero, then the
component of the angular momentum of the system
along that axis ( Lz ) cannot change, no matter what
changes take place within the system.
Substituting
L  I into Li  L f ,we get
I ii  I f  f
(6-96)
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
The law of conservation of angular momentum
Li  L f
I ii  I f  f
Like the other two conservation laws ,
The law of conservation of angular momentum
holds beyond the limitations of Newtonian
mechanics. It holds for particles whose speeds
approach that of light ( where the theory of
relativity reigns) and it remains true in the world
of subatomic particles ( where quantum
mechanics reigns). No exceptions to it have ever
been found !
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
Examples
1. The spinning volunteer
A student + a stool
rotate around z axis.
No external torque acts on
the system, the angular
momentum of the system
must remain constant,
At the beginning, the
student stretches out his
both arms with each hand
holding a dumbbell,
Ii  i 
I ii  I f  f
I f  f 
when the person drops both arms to reduce the moment of
inertia the rotational angular velocity of the person and the
stool is increased.
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
2. The springboard diver
The diver leaves the high-diving
board with outstretched arms and
legs and some initial angular
velocity about his centre of gravity.
His angular momentum ( I )
remains constant since no external
torques act on him (gravity exerts no
torque about his centre of gravity).
To make a somersault he must
increase his angular velocity.
He does this by pulling in his legs
and arms so that decreases I
and therefore increases  . By
extending his arms and legs again,
the diver can enter the water with
little splash.
I i  i 
I ii  I f  f
I f  f 
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
3. Spacecraft orientation
The spacecraft + fiywheel form an
isolated system. Therefore, if the
system's total angular momentum
L is zero, it must remain zero.
To change the orientation of the
spacecraft, the flywheel is made to
rotate. The spacecraft will start
to rotate in the opposite sense to
maintain the system's angular
momentum at zero.
When the flywheel is then brought
to rest, the spacecraft will also stop
rotating but will have changed its
orientation.
6-17 The Angular Momentum of a Rigid
Body Rotating About a Fixed Axis
4. The incredible shrinking star
When the nuclear fire in the core of a star
bums low, the star may eventually begin to
collapse.
I1
1
beforeshrinking
shrinking
before
The collapse may go so far as to reduce
the radius of the star from something like
that of the Sun to the incredibly small value
of a few kilometers. The star then becomes
a neutron star.
During this shrinking process, the star
is an isolated system and its angular
momentum L cannot change. Because its
rotationaI inertia is greatly reduced, its
angular speed is correspondingly greatly
increased, to as much as 600 to 800
revolutions per second.
I11  I 22
2
I2
after
shrinking
The neutron star
6-18 Precession of a Gyroscope
A nonspinning gyroscope fslls downword about the tip of the
support O because of the torque:   Mgr sin 90  Mgr
 net
L
A rapidly spinning gyroscope rotates horizontally about a
vertical axis through support point O in a motion called
precession.
Spinning wheel : L  I , Mg produce a torque:   dL
dt
dL   dt
Only change the direction of L !

6-18 Precession of a Gyroscope
  Mgr sin 90  Mgr
dL   dt
  L Only change the direction of L !
dL // 
L
rotates about z axis, Precession!
dL   dt  Mgrdt
d Mgr


dt
I
dL Mgrdt
d 

L
I
(precession rate)
(6-107)