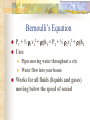Download ap physics b lesson 64, 76 fluid mechanics

Warm-up

For light of a given frequency, ice has an
index of refraction of 1.31 and water has an
index of refraction of 1.33. Find the
critical angle θc for the ray of light at the
ice/water interface.
ice
θc
water
Answer

80º
Problems to skip/add to the HW Sets
Problem Set
Skip
Don't skip
63
11, 12,
13
64
9, 12, 16
65
11, 13, 14, 17
15, 18
Fluid Mechanics
Buoyancy and Pressure
Fluids and Buoyant Force

Fluids



Have no definite shape
Gases do not have definite volume
They flow
Density


Density = mass/volume (kg/m3)
ρ = m/v
Common Densities


Water = 1000kg/m3
Air = 1.29kg/m3

Objects will float if their density is less than
these
Pressure

Force/Area

P=F/A
N/m2 or Pa
 1 N/m2 = 1Pa


Pair = 101,300 Pa
Relationship between ρ, Fg, and P

1m3 of water has a weight of 9800N (1000kg/m3 x 1m3 x
9.8)
 Use 9.8 for all pressure problems
1.0m
9800N
1.0m
1.0m
The pressure on the bottom equals the weight of the cube
P = F/A = 9800N/1.0m2 = 9800Pa
Relationship between ρ, Fg, and P

If we stack three cubes atop one another we get the
following pressure

P = 9800x 3/1.0m2 = 29,400Pa.
Relationship between ρ, Fg, and P


Thus the pressure at a depth in fluid in Pa is numerically
equivalent to the weight of a column of fluid whose cross
sectional area is 1m2.
To find the pressure at any depth in a column of fluid of
any given cross sectional area, the weight per unit
volume is multiplied by the depth!
Relationship between ρ, Fg, and P

Works for gases also!

The average sea level density of air at 25°C and 1 atm is
1.29kg/m3. The density decreases rapidly with altitude. The
total mass of a column of air extending from the top of the
atmosphere down to seal level whose cross sectional area is 1m2
is 10, 330kg and its weight is 101300N. Thus the atmospheric
pressure is 101,300 Pa or 101.3kPa.
Fluid Pressure

P = ρgh
Pressure Varies with Depth


Remember that air pressure is 1.01x105Pa
https://www.youtube.com/watch?v=cEnJIT
nn_4U
Pressure Increasing with Depth


The column of water above you builds as
you go further and further down.
PT = P + Po



PT is the absolute pressure
Po is the atmospheric or original pressure
P is the fluid pressure (pressure from depth)
Gauge Pressure

Gauge Pressure

P g = PT - P o
Example I

On a particular day, the atmospheric
pressure was 101,000 Pa. A) What was the
pressure at a depth of 94.0m below the
surface of the sea? B) What was the gauge
pressure at this depth? The density of
seawater is 1025kg/m3
Answer

1.05x106Pa, 9.49x105Pa
Example II

The fluid in a u-tube is glycerin, whose
density is 1260kg/m3. Atmospheric
pressure is 1.01x105Pa. A) What is the
pressure P in the container? B) What is the
gauge pressure in the container?
Po
gas
Pgas
P14
Px
Px
14cm taller
Answer

1.03x105Pa, 2.0x103Pa
Problems with Pressure

Diving and ascending too fast

The Bends
https://www.youtube.com/watch?v=LfCOnGHhe
ok
Pascal’s Principle
Pascal’s Principle


P1 = F1/A1 and P2 = F2/A2 , but P2 = P1
Therefore

Pincrease = F1/A1 = F2/A2
Example IV

The pressure produced by the force F1 on a
frictionless piston with a cross sectional
area A1 is transmitted through the perfect
fluid. Find the resulting upward force F2
on the piston with area A2. (F1 = 75N and
A1 = 10cm2, A2 = 80cm2)
Answer

600N
Off Topic but Cool

https://www.youtube.com/watch?v=wXCD
eqjWuDg
Buoyancy


Keeps objects afloat
Archimedes’s Principle


The fluid that is displaced by an object that is
submerged is equal to the volume of the
object.
Any object completely or partially submerged
in a fluid experiences an upward buoyant
force equal in magnitude of the weight of the
fluid displaced by the object.
What?????

This means that

FB = ρVfluidg


(density of fluid)(volume of fluid)(9.8)
Buoyant force = weight of the displaced fluid
Buoyancy Extended

No matter what depth the cube is
submerged, the difference in the total force
pressing down on the cube and the total
force pushing up on the cube will always
equal the weight of the volume of water
displaced by the cube!!!!
Further Extensions

Archimedes’ Principle works no matter the
shape of the object. It also works for
hollow objects compared to full objects
(hollow sphere of lead compared to a ball
of lead with the same volume). Both
volumes of lead would have the same
buoyant force acting upon them
Example V

A hollow sphere whose mass is 250kg has
a radius of 1.0m. If it is submerged in salt
water at a depth of 10m by a cable. What
is the tension in the cable? The density of
salt water is 1030kg/m3
Answer

40,000N
Example VI

The rectangular block below is placed in
water and 2.0cm of the block remains
above the water. What is the density of the
block?
10.0cm
10.0cm
40.0cm
Fluids in Motion


Fluid Statics – the study of the
relationships between forces and fluids at
rest.
Fluid Dynamics – the study of the
relationships between moving fluids and
the forces that cause the motion
Fluid Dynamics


When a fluid is in motion in a pipe there
are friction forces at play between the
individual particles of the fluid and
between the fluid and pipe.
If the viscosity is not too great, all particles
follow similar streamlines.
Fluid Dynamics


Streamlines form flow tubes which depict
fluid motion.
Particles in a streamline do not cross paths
with other streamlines in laminar (smooth)
motion
In the figure below we see that the streamlines get closer
together at the middle due to the decrease in area. The fluid is
moving faster at this point.
The streamlines above an airplane wing are closer indicating
greater speed.
Fluids Dynamics

Fluid Flow


Laminar – Smooth and repeating motion
Turbulent – flow becomes irregular

Eddy currents
Ideal Fluids

We will only deal with “ideal fluids”




Nonviscous
The density of the fluid is constant. (cannot
be compressed)
The fluid motion is steady (P, ρ, and v at any
given point does not change).
The flow is streamline and laminar.
So What?????

http://www.youtube.com/watch?v=p08_Kl
TKP50
Flow Rate

Volume of fluid/unit time

Rate = Area x speed of fluid


R = Av
A fluid is pumped into a pipe at a flow rate
of 80cm3/s. If the diameter of the pipe is
1.4cm, what is the average speed of the
fluid at this point?
Making Fluids Flow Faster


Pump it faster (no duh!)
Pinch the hose or make the pipe smaller
Continuity Equation
Continuity Equation

A1v1 = A2v2
Example VII

The radius of a fluid-carrying pipe at a
certain point is 2.0cm and the average
speed of the fluid is 14cm/s. What is the
average speed of the fluid at a point where
the radius is only 1.3cm?
Answer

33cm/s
Warm-Up 4/15/14

Get out your notes and a calculator
Bernoulli’s Principle

The pressure in a fluid decreases as the
velocity increases


This is how lift on an airplane wing works
https://www.youtube.com/watch?v=IDhH91
mfCf8
Bernoulli’s Equation
Bernoulli’s Equation



Based upon conservation of Energy
Flow rate changes when a pipe changes
area (thickness) and elevation.
Pressure + PE/volume + KE/volume =
constant

Sum of pressures before = sum of pressures
after
Bernoulli’s Equation


P1 + ½ 1v12 + gh1 = P2 + ½ 2v22 + gh2
Uses



Pipes moving water throughout a city
Water flow into your house
Works for all fluids (liquids and gases)
moving below the speed of sound
Example VIII

Water whose density is 1000kg/m3flows
through a pipe with a flow rate of 0.80m3/s.
The cross sectional area of the pipe is
initially 0.25m2 and the pressure is 5.2Pa.
The cross sectional area of the pipe
becomes 0.40m2, what is the new pressure
of the fluid.
Answer

3100Pa
Example IX

Ethyl alcohol (ρ = 810kg/m3) has a flow
rate of 0.24m3/s through a pipe whose cross
sectional area is 0.060m2 and in which the
pressure is 9.5x104Pa. The centerline of
the pipes rises 4.0m and the area is reduced
to 0.020m2. What is the fluid pressure in
the elevated pipe?
Answer

11000Pa