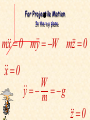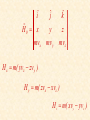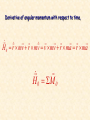Download Kinetics of Particles: Newton`s Second Law

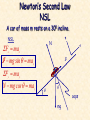
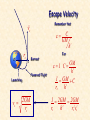
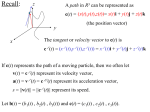
CHAPTER 12
Kinetics of Particles:
Newton’s Second Law
12.1 INTRODUCTION
Reading Assignment
12.2 NEWTON’S SECOND LAW OF
MOTION
If the resultant force acting on a particle
is not zero, the particle will have an
acceleration proportional to the magnitude
of the resultant and in the direction of this
resultant force.
More accurately


F  ma

F  ma
Cause = Effect
Inertial frame
or Newtonian frame of reference –
one in which Newton’s second law equation
holds. Wikipedia definition.
Free Body Diagrams (FBD)
This is a diagram showing some object and the
forces applied to it.
It contains only forces and coordinate
information, nothing else.
There are only two kinds of forces to be
considered in mechanics:
Force of gravity
Contact forces
Example FBD
A car of mass m rests on a 300 incline.
FBD
N
F
y
This completes the FBD.
q
q
mg
x
Example FBD
A car of mass m rests on a 300 incline.
FBD
Just for grins, let’s do
a vector addition.
N
F
q
q
mg
Newton’s Second Law
NSL
A car of mass m rests on a 300 incline.
FBD
NSL
F  ma
F  mg sin q  ma
x
N
x
F
x
F  ma
N  mg cos q  ma
y
y
y
What if friction is smaller?
q
q
mg
Newton’s Second Law
NSL
A car of mass m rests on a 300 incline.
NSL
N
F  ma
F  mg sin q  ma
x
x
F
x
F  ma
N  mg cos q  ma
y
y
y
q
q
oops
mg
12.3 LINEAR MOMENTUM OF A PARTICLE.
RATE OF CHANGE OF LINEAR
MOMENTUM



dv d
F  m  ( mv )
dt dt


L  mv  Linear Momentum

 dL 
F 
L
dt
Linear Momentum Conservation Principle:
If the resultant force on a particle is
zero, the linear momentum of the particle
remains constant in both magnitude and
direction.
 
F  L  0

L  Cons tan t
12.4 SYSTEMS OF UNITS
Reading Assignment
12.5 EQUATIONS OF MOTION
Rectangular Components
 ( Fx î  Fy ˆj  Fz k̂ )  m( a x î  a y ˆj  a z k̂ )
or
Fx  max  mx
Fy  may  my
Fz  maz  mz
y
For Projectile Motion
In the x-y plane
mx  0 my  W mz  0
O
x
z
x  0
W
y     g
m
z  0
Tangential and Normal Components
Ft  mat

m
at
F
y
Fn  man

m
an
F
m
x
And as a reminder
O
z
dv
Ft  m
dt
v
2
Fn  m 
12.6 DYNAMIC EQUILIBRIUM
Take Newton’s second law,


F  ma


F  ma  0
This has the appearance of being
in static equilibrium and is actually
referred to as dynamic equilibrium.
Don’t ever use this method in my course … H. Downing
12.7 ANGULAR MOMENTUM OF A
PARTICLE. RATE OF CHANGE OF
ANGULAR MOMENTUM

mv
y



H 0  r  mv
H 0  rmv sin 

HO


r
x
O
z
Angular Momentum of a Particle



H 0  r  mv
moment of momentum or the
angular momentum of the
particle about O. It is
perpendicular to the plane
containing the position vector
and the velocity vector.
î

H0  x
mvx
ˆj
y
mv y
k̂
z
mvz
H x  m( yvz  zv y )
H y  m( zv x  xvz )
H z  m( xvy  yvx )
For motion in x-y plane
H x  m( yvz  zv y )  0
y
H y  m( zv x  xvz )  0

H z  m( xvy  yvx )
In Polar Coordinates

mvq

mv

r

mvr
x
O
H 0  rmv sin   rmvq  mr q
2
Derivative of angular momentum with respect to time,


 
 

 
 
H 0  r  mv  r  mv  v  mv  r  ma  r  ma


H 0  M 0
12.8 EQUATIONS OF MOTION IN
TERMS OF RADIAL AND
TRANSVERSE COMPONENTS
Consider particle at r and q, in polar
coordinates,
Fr  mar
Fq  maq
 mr  rq 
 mrq  2rq 

Fq
2
y

Fr
This latter result may also be
derived from angular momentum.

r
q
O
x
Fr  mar  mr  rq 2 
Fq  maq  mrq  2rq 
This latter result may also be
derived from angular momentum.
H O  mr q

Fq
2

y

d
rFq 
mr 2q
dt
2 
 m r q  2rrq

Fq  mrq  2rq 


Fr

r
q
O
x
12.9 MOTION UNDER A CENTRAL
FORCE. CONSERVATION OF
ANGULAR MOMENTUM
When the only force acting on particle is directed
toward or away from a fixed point O, the particle is said
to be moving under a central force.
Since the line of action of the central force
passes through O,
y


 M O  HO  0

F
Position vector and motion of particle are in
a plane perpendicular to

HO
O
m
x




H 0  0  H  Constant  r  mv
Position vector and motion of particle
are in a plane perpendicular to

HO
Since the angular momentum is constant,
its magnitude can be written as
y
r0 mv0 sin 0  rmv sin 

F
Remember
mr q  H
2
o
H0
2 

r
q

h
m
O
m
x
Conservation of Angular Momentum
rdq
y
dA
dq
q
O

r

F
x
P
• Radius vector OP sweeps infinitesimal
area
dA  12 r 2 dq
• Areal velocity
dA  1 r 2 dq  1 r 2q
2
2
dt
dt
• Recall, for a body moving under a central
force,
h  r q  constant
2
• When a particle moves under a central
force, its areal velocity is constant.
12.10 NEWTON’S LAW OF GRAVITATION
• Gravitational force exerted by the sun on a
planet or by the earth on a satellite is an
important example of gravitational force.

r
M

-F
m

F
• Newton’s law of universal gravitation - two
particles of mass M and m attract each other
with equal and opposite forces directed along
the line connecting the particles,
F G
Mm
r2
G  cons tant of int egration
3
m
11
2
2

6
.
67

10
N

m
/
kg
 66.7  10 12
kg  s 2
4
ft
8
2
2

3
.
44

10
lb

ft
/
sl
 34.4  10 9
lb  s 4
• For particle of mass m on the earth’s surface,
GM
g  9.81 m / s 2  32.2 ft / s 2
W  m 2  mg
r
12.11 TRAJECTORY OF A PARTICLE
UNDER A CENTRAL FORCE
For particle moving under central force directed towards force center,


m r  rq 2   F r  F


m rq  2rq   Fq  0
Second expression is equivalent to
r 2q  h  constant ,
h

q 2
r
dr dr dq
h dr
d
r 

 2
 h
dq
dt dq dt r dq
Remember that
1
 
r
h

q 2
r
h2 d 2  1 
dr h dr
r 
 2
 2
2  
r dq  r 
dt r dq
Let
1
u
r
2
d
u
2 2
r  h u
2
dq
Remember that


m r  rq 2   F
2
d
u
2 2
r  h u
dq 2


m r  rq 2   F
 2 2 d 2u
2 3
m  h u
 h u    F
2
dq


d 2u
F
u 
2
dq
mh2u 2
This can be solved, sometimes.
If F is a known function of r or u, then particle trajectory
may be found by integrating for u = f(q ), with constants of
integration determined from initial conditions.
12.12 APPLICATION TO SPACE
MECHANICS
Consider earth satellites subjected to only
gravitational pull of the earth.
GMm
F  2  GMmu 2
r
r
O
q
A
d 2u
F
u 
2
dq
mh2u 2
d 2u
GM
u  2
2
dq
h
d 2u
GM
u  2
2
dq
h
There are two solutions:
General Solution
Particular Solution
r
O
q
A
GM 1
u  C cos( q  q0 ) 2  r
h
From the figure choose polar axis so that
q0  0
The above equation for u is a conic section,
that is it is the equation for
ellipses (and circles), parabolas, and hyperbolas.
Conic Sections
Circle
Ellipse
Parabola
Eccentricity
C

GM
Hyperbola
h2
GM 1
u  C cos( q  q0 ) 2  r
h
1  GM  C cos q  GM 1   cos q 
r
h2
h2
Origin, located at earth’s center,
r
O
is a focus of the conic section.
q
A
Trajectory may be ellipse, parabola, or hyperbola
depending on value of eccentricity.
 1
1  GM 1   cos q 
r
h2
Hyperbola, e > 1 or C > GM/h2.
The radius vector becomes
infinite for
q1
r
q
O
A
q1
1   cos q1  0
 GM 
 1
1

q1   cos       cos  
2 


 Ch 
1
 1
1  GM 1   cos q 
r
h2
Parabola,  = 1 or C = GM/h2.
q2
The radius vector becomes
infinite for
r
q
O
A
1  cos q 2  0
q  180
2
0
1  GM 1   cos q 
r
h2
Ellipse,  < 1 or C < GM/h2.
 1
The radius vector is finite for
all q, and is constant for a
circle, for  = 0.
r
O
q
A
r0 v0  h
and

v0
O
r0
A
2
GM  GM  gR
h2
r02 v02 r02 v02
Burnout
Integration constant C is
determined by conditions at
beginning of free flight, q =0,
r = r0 .
Powered Flight
Launching
1 GM
r0  h 2  C
1 GM
C  2
r0
h
Escape Velocity

v0
O
Remember that

C
GM
h
2
For
r0
A
Launching
v0  2GM
r0
Burnout
Powered Flight
  1 C  GM
h2
1  GM  C
2
r0
h
1  2GM  2GM
r0
h2
r02 v02
If the initial velocity is less than the
escape velocity, the satellite will
move in elliptical orbits.
If  = 0, then
 1

r
O
q
C
GM
0
h
2
A
1  GM  C
r0
h2
GM
vcircle 
r0
1  GM  GM
r0
h2
r02 v02
Recall that for a particle moving under a
central force, the areal velocity is constant,
i.e.,
B
dA  1 r 2q  1 h  constant
2
2
dt
a
b
A’
O’
C
O
A
Periodic time or time required
for a satellite to complete an
orbit is equal to the area
within the orbit divided by
areal velocity,
 ab
2 ab


h2
h
Where
r1
r0
a  21 r0  r1 
b  r0 r1
12.13 KEPLER’S LAWS OF PLANETARY
MOTION
• Results obtained for trajectories of satellites around earth
may also be applied to trajectories of planets around the sun.
• Properties of planetary orbits around the sun were
determined by astronomical observations by Johann Kepler
(1571-1630) before Newton had developed his fundamental
theory.
1) Each planet describes an ellipse, with the sun located at
one of its foci.
2) The radius vector drawn from the sun to a planet sweeps
equal areas in equal times.
3) The squares of the periodic times of the planets are
proportional to the cubes of the semimajor axes of their
orbits.