Download File

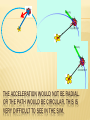
CIRCULAR MOTION AND GRAVITATION
Angular Measure, Angular Speed,
and Angular Velocity
BELLWORK
1. A tube is been placed upon the
1 m-high table and shaped into a
three-quarters circle. A golf ball is
pushed into the tube at one end
at high speed. The ball rolls
through the tube and exits at the
opposite end. Describe the path
of the golf ball as it exits the tube.
2. If the 50g golf ball leaves the
tube with a velocity of 32 m/s at
45o, a) what is it’s maximum
height, b) how long does it take to
land, and c) what is the impulse
force the ground exerts on the
ball to bring it to a stop in 98 μs?
ALGEBRA 2 REVIEW




An arc of a circle is a "portion" of the
circumference of the circle.
The length of an arc is simply the length of its
"portion" of the circumference. Actually, the
circumference itself can be considered an arc length.
The length of an arc (or arc length) is traditionally
symbolized by s.
The radian measure of a central angle of a circle
is defined as the ratio of the length of the
arc the angle subtends, s, divided by the
radius of the circle, r.
ALGEBRA 2 REVIEW, CONT.
Relationship between Degrees and Radians:
 When the arc length equals an entire
circumference, we can use s = θr to get 2πr= θr
and 2π = θ.
 This implies that 2π = 360o
 So
and

To change
from degrees to radians,
multiply by
To change
from radians to degrees,
multiply by
EXAMPLE PROBLEMS
1.
2.
3.
Convert 50º to radians.
Convert π/6 radians to degrees.
How long is the arc subtended by an angle of
7π/4 radians on a circle of radius 20.000 cm?
Answers:
1. 5π/18 radians
2. 30 degrees
3. 109.96 cm
ANGULAR MEASURE
Circular motion is described using
polar coordinates, (r, q)
 x=rcosq and y = rsinq, where q is
measured counterclockwise (ccw)
from the positive x-axis.
 Angle is defined as q = s/r, where s is the arc
length, r is the radius, and q is the angle in
radians. Also expressed as s=rq
 Angular distance, Δq = q - qo is measured in
degrees or radians. A radian is the angle that
subtends an arc length that is equal to the
radius (s=r)
 1 rad = 57.3o , or 2rad = 360o

EXAMPLE 1

When you are watching the NASCAR Daytona
500, the 5.5 m long race car subtends an
angle of 0.31o . What is the distance from the
race car to you?
SOLUTION TO EXAMPLE 1
UNIFORM CIRCULAR MOTION IS THE MOTION OF
AN OBJECT IN A CIRCLE WITH A CONSTANT OR
UNIFORM SPEED.
 When moving in a circle, an object traverses a
distance around the perimeter of the circle
 The distance of one complete cycle around the
perimeter of a circle is known as the
circumference
 This relationship between the circumference of
a circle, the time to complete one cycle around
the circle, and the speed of the object is merely
an extension of the average speed equation
COMBINING KINEMATICS AND CIRCULAR
MEASUREMENT TO CALCULATE SPEED
The circumference of any circle can be
computed using from the radius according to
the equation
Circumference = 2*pi*Radius
 relating the speed of an object moving in
uniform circular motion to the radius of the
circle and the time to make one cycle around
the circle (period, T), where R=radius:

ANGULAR SPEED AND VELOCITY

Instantaneous angular speed is the magnitude of
the instantaneous angular velocity

Tangential (linear) speed and angular speed are
related to each other through
where r is the radius.
 The time it takes for an object to go through one
revolution is called the period, T.
 Then number of revolutions in one second is
called the frequency, f
THE DIRECTION OF THE VELOCITY VECTOR
Velocity, being a vector,
has both a magnitude
and a direction
 Since an object is
moving in a circle, its
direction is continuously
changing
 direction of the velocity
vector is tangential to
the circular path

EXAMPLE 2

A bicycle wheel rotates uniformly through 2.0
revolutions in 4.0 s.
a) What is the angular speed of the wheel?
b) What is the tangential speed of a point
0.10 m from the center of the wheel?
c) What is the period?
d) What is the frequency?
ACCELERATION
an accelerating object is an object which is
changing its velocity.
 a change in either the magnitude or the
direction constitutes a change in the velocity.
 an object moving in a circle at constant speed
is accelerating because the direction of the
velocity vector is changing.

CHANGE IN VELOCITY
The acceleration of the object is in the same
direction as the velocity change vector
 Objects moving in circles at a constant speed
accelerate towards the center of the circle.

CENTRIPETAL ACCELERATION
The linear tangential velocity vector changes
direction as the object moves along the circle.
 This acceleration is called centripetal
acceleration (center-seeking) because it is
always directed toward the center of the circle.
 The magnitude of centripetal acceleration is
given by

CENTRIPETAL FORCE
From Newton’s Second Law, we conclude that
there MUST be a net force associated with
centripetal acceleration.
 Centripetal force is always directed toward the
center of the circle since the net force on an
object is in the same direction as acceleration.

EXAMPLE 3

A car of mass 1500 kg is negotiating a flat
circular curve of radius 50 m with a speed of
20 m/s.
a) What is the source of the centripetal force
on the car? Explain
b) What is the magnitude of the centripetal
acceleration of the car?
c) What is the magnitude of the centripetal
force on the car?
d) What is the minimum coefficient of static
friction between the car and the curve?
WARM-UP

Convert the following angles from degrees to
radians or from radians to degrees, to two
significant figures.
 -285o
 195o
 -90o
 -4/3 π
 -270o
 -3/4 π
 165o
 π/3
CONVERT THE FOLLOWING ANGLES FROM
DEGREES TO RADIANS OR FROM RADIANS TO
DEGREES, TO TWO SIGNIFICANT FIGURES.
 -285o
 -5 rad or 1.6 π
 195o
 3.4 rad or 1.08 π
 -90o
 -1.6 rad or π/2 rad
 -4/3 π
 -240o or4/3 π rad
 -270o
 -4.7 rad or 3/2 π rad
 -3/4 π
 -135o or 3/4 π rad
 165o
 2.9 rad or 0.92 π rad
 π/3
 60o or π/3 rad
EXAMPLE 4: AFTER CLOSING A DEAL WITH A
CLIENT, KENT LEANS BACK IN HIS SWIVEL CHAIR
AND SPINS AROUND WITH A FREQUENCY OF 0.5
HZ. WHAT IS KENT’S PERIOD OF SPIN?
Given: f = 0.5 Hz
 Solve: T = 1/f
T= 1/0.5 Hz
T= 2 s

EXAMPLE 5: CURTIS’ FAVORITE DISCO RECORD
HAS A SCRATCH 12 CM FROM THE CENTER THAT
MAKES THE RECORD SKIP 45 TIMES EACH
MINUTE. WHAT IS THE LINEAR SPEED OF THE
SCRATCH AS IT TURNS?
The record makes 45 revolutions every minute
(60 s), so T = 60 s/45 rev. = 1.3 s
 r = 12 cm
 v = 2πr/T

= 2π(12cm)/1.3s
 = 58 cm/s

EXAMPLE 6: MISSY’S FAVORITE RIDE AT THE
TOPSFIELD FAIR IS THE ROTOR , WHICH HAS A
RADIUS OF 4.0 M. THE RIDE TAKES 2.0 S TO
MAKE ON E FULL REVOLUTION.
A) WHAT IS MISSY’S LINEAR SPEED ON THE
ROTOR?
B) WHAT IS MISSY’S CENTRIPETAL
ACCELERATION ON THE ROTOR?
Given: r = 4.0 m, T = 2.0s
 v=2pir/T = 2pi(4.0m)/2.0s = 13 m/s
 ac = v2/r = 132/4.0 m = 42 m/s2

THE CAUSE OF CENTRIPETAL FORCE
In order to have an acceleration, there MUST be
a force
 What provides that force?

Tension
Applied Force
Friction
Spring Force
Gravitational Force
WHAT HAPPENS WHEN THE FORCE VANISHES?
MOTION IN A HORIZONTAL CIRCLE
The speed at which the object moves depends
on the mass of the object and the tension in
the cord
 The centripetal force is supplied by the tension

CIRCULAR MOTION ABOUT A CONICAL PENDULUM
The object is in equilibrium in the vertical
direction and undergoes uniform circular
motion in the horizontal
direction
 v is independent of m

HORIZONTAL (FLAT) CURVE
The force of static friction
supplies the centripetal force
 The maximum speed at
which the car can negotiate
the curve is

BANKED CURVE

There is a component of
the normal force that
supplies the centripetal
force
FICTIONAL FORCES
From the frame of the passenger (b),
a force appears to push her toward the
door
 From the frame of the Earth, the car
applies a leftward force on the
passenger
 The outward force is often called a
centrifugal force
 It is a fictitious force due to the
acceleration associated with the car’s
change in direction

THE GREAT MISCONCEPTION
Centrifugal, not to be confused with centripetal,
means away from the center or outward.
 Circular motion leaves the moving person with
the sensation of being thrown OUTWARD from
the center of the circle rather than INWARD
 It’s really just inertia!
 http://www.physicsclassroom.com/mmedia/cir
cmot/cf.cfm

EFFECTS OF “PRETEND” FORCES
Although fictitious forces are not real forces, they
can have real effects
 Examples:
 Objects in the car do slide
 You feel pushed to the outside of a rotating
platform
 The Coriolis force is responsible for the rotation of
weather systems and ocean currents

LOOP – THE – LOOP – A VERTICAL CIRCLE
At the bottom of the
loop, the upward force
experienced by the
object is greater than
it’s weight
 Centripetal Force
Vector ADDS to Normal
Force Vector

LOOP – THE – LOOP
At the top of the
circle, the force
exerted on the object
is less than its
weight
 Centripetal Force
Vector TAKES AWAY
from the normal
force

WARM-UP:
Captain Chip, the pilot of a 60500 kg jet plane,
is told he must remain in a holding pattern over
the airport until it is his turn to land. If Captain
Chip flies his plane in a circle whose radius is
50.0 km once every 30.0 min, what centripetal
force must the air exert against the wings to
keep the plane moving in a circle?
EXAMPLE 7.45
Many racetracks have banked turns, which
allow the cars to travel faster around the curves
than if the curves were flat. Actually, cars could
also make turns on these banked curves if
there were no friction at all.
 Use a free body diagram to explain how this is
possible.

EXAMPLE 7.46

An indy car with a speed of 120 km/hr goes
around a level, circular track with a radius of
1.00 km. What is the centripetal acceleration
of the car?
A. 1.11 m/s2
B. 0.555 m/s2
C. 3.49 m/s2
D. 7.54 m/s2
.
EXAMPLE 7.52
A car with a constant speed of 83.0 km/hr
enters a circular flat curve with a radius of
curvature of 0.400 km. If the friction between
the road and the car’s tires can supply a
centripetal acceleration of 1.25 m/s2 does the
car negotiate the curve safely? Justify your
answer.
A. Yes
B. No

EXAMPLE 7.53

A student is to swing a bucket of
water in a vertical circle without
spilling any (Fig. 7.29).
(a) Use a free body diagram to
help explain how this task is
possible (what provides the
centripetal force?).
(b) If the distance from his
shoulder to the center of mass
of the bucket of water is 1.0 m,
what is the minimum speed
required to keep the water from
coming out of the bucket at the
top of the swing?
EXAMPLE 7.58

For a scene in a movie, a
stunt driver drives a
1.50 x 103 kg SUV with a
length of 4.25 m around a circular curve with a
radius of curvature of 0.333 km (Fig. 7.31).
The vehicle is to be driven off the edge of a
gully 10.0 m wide, and land on the other side
2.96 m below the initial side. What is the
minimum centripetal acceleration the truck
must have in going around the circular curve to
clear the gully and land on the other side?
BELLWORK: BONNIE IS ICE SKATING AT THE
OLYMPIC GAMES. SHE IS MAKING A SHARP TURN
WITH A RADIUS OF 22.6 M AND WITH A SPEED OF
16.1 M/S. USE NEWTON'S SECOND LAW TO
DETERMINE THE ACCELERATION AND THE ANGLE
OF LEAN OF BONNIE'S 55.0-KG BODY.
Given Info:
m = 55.0 kg
v = 16.1 m/s
r = 22.6 m
Find:
a = ???
Angle of lean = ???
SOLUTION TO BELLWORK
ac = v2/R a = (16.1 m/s)2/(22.6 m)
= 11.5 m/s2
 Fx = Fnet = m•a Fx
= (55.0 kg)•(11.5 m/s/s)
= 631 N


ANGULAR ACCELERATION:
NON-UNIFORM CIRCULAR MOTION

Angular acceleration = the rate of change of
angular velocity
EXAMPLE 8: A ROTATING CD

A CD accelerates uniformly from rest to its
operational speed of 500 rpm in 3.50 s.
A. What is the angular acceleration of the CD
during this time?
B. What is the angular velocity of the CD after
this time? The angular acceleration after
this time?
C. If the CD comes uniformly to a stop in 4.50
s, what is its angular acceleration during
that part of the motion?
1. WHAT COULD THE POSITION AND VELOCITY
VECTORS FOR THE LADY BUG LOOK LIKE?
A.
B.
C.
D.
2. WHAT COULD THE ACCELERATION AND
VELOCITY VECTORS LOOK LIKE?
A.
B.
C.
D.
3. WHAT COULD THE POSITION &
ACCELERATION VECTORS LOOK LIKE?
A.
B.
C.
D.
THE ACCELERATION WOULD NOT BE RADIAL
OR THE PATH WOULD BE CIRCULAR. THIS IS
VERY DIFFICULT TO SEE IN THE SIM.
4. IF YOU HAD TWO BUGS MOVING IN
CIRCLES LIKE THIS, WHAT COULD THE
VELOCITY VECTORS AT POINT X VS POINT Y
LOOK LIKE?
X
Y
A
B
C
D Any of the above
E None of the above
are possible
X
Y
X
Y
IF THEY WERE CONNECTED WITH A BAR SO THEY
HAD TO GO AROUND TOGETHER, IT WOULD BE LIKE
IN LADYBUG REVOLUTION, BUT OTHERWISE THERE
IS NO WAY TO KNOW THE LENGTH RELATIONSHIP,
BUT THE VECTORS WOULD BE PARALLEL
SEE FIG 7.14, P. 230
The acceleration and force
have tangential
components
 Fc produces the centripetal
acceleration
 Fτ produces the tangential
acceleration
ΣF = ΣFc + ΣFτ

TANGENTIAL ACCELERATION

The tangential acceleration is the rate of
change of tangential velocity
For non-uniform circular motion, there are
angular and tangential acceleration.
 The total acceleration is the vector sum of the
tangential and centripetal accelerations.

EXAMPLE 7.60 THE ANGULAR ACCELERATION IN
CIRCULAR MOTION :
(a) is equal in magnitude to the tangential
acceleration divided by the radius
 (b) increases the angular velocity if both
angular velocity and angular acceleration are in
the same direction
 (c) has units of s-2
 (d) all of the preceding.

EXAMPLE 7.62: FOR UNIFORM CIRCULAR
MOTION,
 (a)
α=0
 (b) ω = 0
 (c) r = 0
 (d) none of the preceding.
EXAMPLE 7.66

During an acceleration, the angular speed of an
engine increases from 600 rpm to 2500 rpm in
3.0 s. What is the average angular acceleration
of the engine?
TORQUE: MEASUREMENT OF THE TENDENCY OF A
FORCE TO PRODUCE A ROTATION ABOUT AN AXIS.
 Torque
= perpendicular force x lever arm
τ=F x d
 d = distance from the pivot point, or
fulcrum, to the point where the
component of the force perpendicular to
the lever arm is being exerted
 The longer the lever arm, the larger the
torque
Counterclockwise rotation = POSITIVE τ
 Clockwise rotation = NEGATIVE τ
 Units = Newton x meter = Nm (but NOT equal to
Joules because torque is not a form of energy)
 NOTE: weight is a force that can produce torque
if the object is not supported at its center of
gravity.

EXAMPLE 1

Ned tightens a bolt in his car engine by exerting
12 N of force on his wrench at a distance of
0.40 m from the fulcrum. How much torque
must Ned produce to turn the bolt?
EXAMPLE 2:

Mabel and Maude are seesawing on the school
playground and decide to see if they can move
to the correct location to make the seesaw
balance. Mabel weighs 400 N and she sits
2.00 m from the fulcrum of the seesaw. Where
should 450-N Maude sit to balance the
seesaw?
ANGULAR MOMENTUM: MEASURE OF HOW
DIFFICULT IT IS TO STOP A ROTATING OBJECT
Moment of Inertia: The resistance of an object
to changes in its rotational motion
moment of inertia = (mass)(radius)2
I = mr2
 SI Units = kilogram meter squared = kgm2
 An object that is rotating tends to continue to
spinning at a constant rate unless acted on by
an unbalanced force to alter that rotation

MOMENT OF INERTIA FOR VARIOUS SHAPES
Hoop rotating about its center
Hoop rotating about its diameter
Solid cylinder
Stick rotating about its center of
gravity
Stick rotating about its end
Solid sphere rotating about its
center of gravity
I=mr2
I = ½ mr2
I = ½ mr2
I = 1/12 ml2
I = 1/3 ml2
I = 2/5 mr2
ANGULAR MOMENTUM
Angular momentum = (mass)(velocity)(radius)
L = mvr
 SI Units = kilogram meter2 per second2
 kgm2/s2
 The product of the mass and the velocity for an
object rotating at a distance, r, from the axis.
 Angular Momentum of a system is conserved
when no outside forces are acting
EXAMPLE 3

On the Wheel of Fortune game show, Ian spins
the 15.0 kg wheel that has a radius of 1.40 m.
What is the moment of inertia of this diskshaped wheel? (thin cylinder)
EXAMPLE 4

Jun is twirling her 0.60 m majorette’s baton
that has a mass of 0.40 kg. What is the
moment of inertia of the baton as it spins
about its center of gravity?
EXAMPLE 5
At Wellesley College in
Massachusetts there is a
favorite tradition called hoop
rolling. In their caps and gowns,
seniors roll wooden hoops in a
race in which the winner is said
to be the first in the class to
marry. Hilary rolls her 0.2 kg
hoop across the finish line. The
moment of inertia of the hoop
is 0.032 kgm2 . What is the
radius of the hoop?
EXAMPLE 6

Jupiter orbits the sun with a speed of 2079 m/s
at an average distance of 71,398,000 m.
If Jupiter has a mass of 1.90 x 1027 kg, what is
its angular momentum as it orbits?