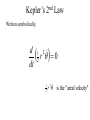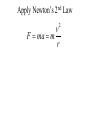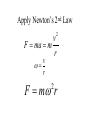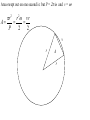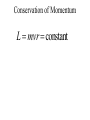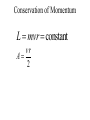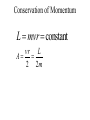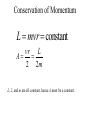* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Document
History of Mars observation wikipedia , lookup
Observational astronomy wikipedia , lookup
Discovery of Neptune wikipedia , lookup
Patronage in astronomy wikipedia , lookup
Lunar theory wikipedia , lookup
Tropical year wikipedia , lookup
Astrobiology wikipedia , lookup
Rare Earth hypothesis wikipedia , lookup
Aquarius (constellation) wikipedia , lookup
Astronomical unit wikipedia , lookup
De revolutionibus orbium coelestium wikipedia , lookup
Planets beyond Neptune wikipedia , lookup
Late Heavy Bombardment wikipedia , lookup
Exoplanetology wikipedia , lookup
Planetary system wikipedia , lookup
History of astronomy wikipedia , lookup
IAU definition of planet wikipedia , lookup
History of Solar System formation and evolution hypotheses wikipedia , lookup
Johannes Kepler wikipedia , lookup
Formation and evolution of the Solar System wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Satellite system (astronomy) wikipedia , lookup
Definition of planet wikipedia , lookup
Planetary habitability wikipedia , lookup
Extraterrestrial life wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
Kepler (spacecraft) wikipedia , lookup
Copernican heliocentrism wikipedia , lookup
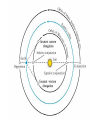
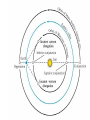
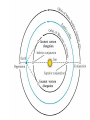
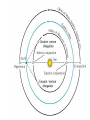
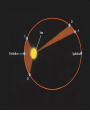
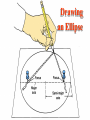
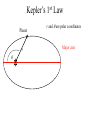
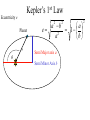
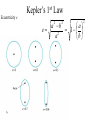
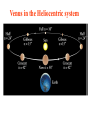
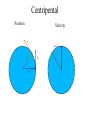
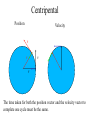
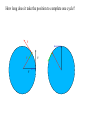
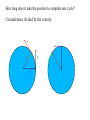
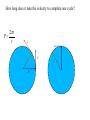
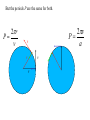
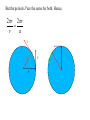
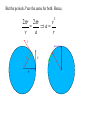
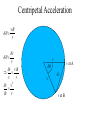
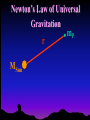
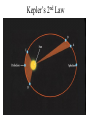
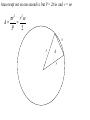
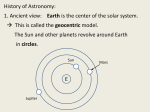
OUR UNIVERSE WEEK 2 Lectures 4 - 6 LEARNING GOALS 1. Understand the difference between geocentric and heliocentric cosmogonies. Understand the Ptolemaic system and how the Copernican heliocentric system better explains our observations of the Moon and planets. 2. Know how Tycho Brahe revolutionized the practice of astronomy. Know Kepler's three laws and be able to explain them. Understand how Galileo's telescopic observations supported a heliocentric cosmogony. 3. Know Newton's three laws of motion and be able to give examples of each. Know Newton's universal law of gravitation. Be able to explain how Newton used his laws of motion and gravity to obtain Kepler's laws. Astronomy seems to have Astronomy seems to have been practised by been practised by most ancient civilisations. most ancient civilisations. Many ideas, myths and Many ideas, myths and misconceptions misconceptions haveand occurred have occurred over over. We follow over a Western and history over. from the Ancient (400 BC to thethe present) We follow Greeks a Western history from Ancient Greeks (400 BC to the present) Gravitation & Planetary Motion or The Copernican Revolution Geocentric versus Heliocentric cosmogony Explains diurnal motion of stars Sun & Moon rotate with celestial sphere, Def. A theory of the Earth's but also drift place in the Universe slowly with respect to stars. The Geocentric cosmogony Explains diurnal motion of stars Merry-go-round analogy Sun & Moon rotate with celestial sphere, but also drift slowly with respect to stars. Gravitation & Planetary Motion The key difficulty is theMARS retrograde motion of the planets (wanderers) In the geocentric view this required epicycles July 2005 to February 2006 Mars’ retrograde motion MARS Aristotle (384-322 BC) • Earth does not feel as if it’s moving • Natural state for any body is to be stationary •The circle: the perfect form • Cycles & epicycles required Geocentric explanation of retrograde motion Ptolemy (140 AD) in Alexandria’s Library set up precise epicycles to fit the observed planetary motions. Geocentric explanation of retrograde motion Ptolemy (140 AD) in Alexandria’s Library set up precise epicycles to fit the observed planetary motions. Ptolemy (140 AD) • Refined the geocentric model to a high degree •Very accurate, but also very complicated - 80 circles! •Refinements kept being added to account for data. •No coherent theory behind it. Ptolemey’s 13 -Volume Almagest covered elements of spherical astronomy, solar, lunar, and planetary theory, eclipses, and the fixed stars. It remained the definitive authority on its subject for nearly 1500 years. Nicolaus Copernicus (1473 - 1543) Polish Polymath: Lawyer, physician, economist, canon of the church, and artist. Gifted in Mathematics and influenced by the ideas of Aristarchus, he turned to Astronomy in the early 1500’s. Nicolaus Copernicus (1473 - 1543) The heliocentric model explains retrograde motion easily. Nicolaus Copernicus (1473 - 1543) Worked out many details: Ordering of planetary orbits. • Mercury & Venus, Inferior planets, always seen near Sun. • Mars, Jupiter, Saturn, Superior planets, sometimes seen on opposite side of the celestial sphere to Sun, high above horizon - Earth between Sun and these planets. Nicolaus Copernicus (1473 - 1543) Explained why planets appear in different parts of the sky on different dates • Mercury & Venus, Inferior planets, seen in west near Sunset, then in east just before sunrise - elongation. • Mars, Jupiter, Saturn, Superior planets, best seen at night in opposition. • Conjunction: The Earth, Sun and a Planet form a straight line in the direction of the Sun (as seen from the Earth) • Opposition: The Earth, Sun and a Planet form a straight line in the direction away from the Sun (as seen from the Earth, • Inferior Planets: Inferior planets can never be in opposition (they are cannot be away from the sun as seen from the earth). • Two Types of Conjunction: Inferior conjunction (same side as the earth) Superior conjunction (opposite side) • Elongation of a Planet Elongation is the angular distance of an inferior planet from the Sun as seen from the earth. • Elongation of Inferior Planets: Greatest Elongation is the maximum angular distance of an inferior planet from the Sun. Mercury 18o – 28o Venus45o – 47o (eliptical orbits) If visible in the morning: (Eastern Elongation) If visible in the evening: (Western Elongation) Minimum Elongation occurs at …….? • Elongation of Inferior Planets: Greatest Elongation is the maximum angular distance of an inferior planet from the Sun. Mercury 18o – 28o Venus45o – 47o (eliptical orbits) If visible in the morning: (Eastern Elongation) If visible in the evening: (Western Elongation) Minimum Elongation occurs at conjunction (0o either inferior or superior) • Elongation of Superior Planets: The minimum elongation of a superior planet occurs at conjunction (= zero degrees) The greatest elongation of a superior planet occurs at opposition ( = 180o) Elongation Period • Greatest elongations of a planet happen periodically, with a eastern followed by western, and vice versa. • The period depends on the relative angular velocity of Earth and the planet, as seen from the Sun. • The time it takes to complete this period is the synodic period of the planet. Elongation Period Let T be the period between successive greatest elongations, ω be the relative angular velocity, ωe Earth's angular velocity and ωp the planet's angular velocity. Then Elongation Period T 2 Hence Elongation Period T 2 But ω = ωp – ωe Hence Elongation Period T Hence 2 But ω = ωp – ωe Hence 2 T p e Elongation Period Since Then 2 T Hence 2 T 2 2 Tp Te Tp/e are the siderial periods Elongation Period Since Then 2 T Hence Te 2 T 2 2 Te T p Te Tp 1 Tp/e are the siderial periods Elongation Period Since Then 2 T Hence Te 2 T 2 2 Te T p Te Tp 1 Tearth = 365 days: Tvenus = 225 days: T = 584 days Relationship between synodic and siderial periods • Copernicus devised a mathematical formula to calculate a planet's sidereal period from its synodic period. Relationship between synodic and siderial periods • Copernicus devised a mathematical formula to calculate a planet's sidereal period from its synodic period. • E = siderial period of the Earth • P = siderial period of the Planet • S = the synodic period. Relationship between synodic and siderial periods • During the time S, the Earth moves over an angle of (360°/E)S (assuming a circular orbit) and the planet moves (360°/P)S. Relationship between synodic and siderial periods • Let us consider an inferior planet. which will complete one revolution before the earth by the time the two return to the same position relative to the sun. Relationship between synodic and siderial periods S S 360 360 360 P E Relationship between synodic and siderial periods S S 360 360 360 P E SP 360S 360 P E SP S P E P P 1 E S 1 1 1 P E S Relationship between synodic and siderial periods S S 360 360 360 P E SP 360S 360 P E SP S P E P P 1 E S 1 1 1 1 1 1 : For Superior Planets P E S P E S for interval inferiorbetween planetsuccessive S is observed as time overtakings of one planet by the other. for superior planet just swap: 1 E 1 P 1 P 1 E 1 S 1 S E ↔P for superior planet Box 4-1 Nicolaus Copernicus (1473 - 1543) Determined planetary distances from Sun by geometry in terms 1 AU Planet------Copernicus---Modern Mercury 0.38 AU 0.39 AU Venus 0.72 AU 0.72 AU Mars 1.52 AU 1.52.AU Jupiter 5.22 AU 5.20 AU Saturn 9.07 AU 9.54 AU Nicolaus Copernicus (1473 - 1543) • His results showed that the larger the orbit, the longer the period & the smaller the speed. • Noticed variable speed on orbits and so included epicycles to keep using circular motion! • This made his model no better than Ptolemy’s geocentric one to astronomers at the time. MORE EVIDENCE NEEDED Copernicus’ De Revolutionibus Orbium Coelestium (1543, year of his death) On the Revolutions of the Celestial Spheres Tycho Brahe (1546 - 1601) Danish Astronomer: Observed Supernova Nov. 11, 1572 Danish king financed observatory Uraniborg (sky castle) on Hven Island. Made measurements of stars and planets with unprecedented accuracy. Repeated measurements with different instruments to assess errors - pioneer of our modern practices. Tycho Brahe (1546 - 1601) Danish Astronomer: Observed Supernova Nov. 11, 1572 Danish king financed observatory Uraniborg (sky castle) on Hven Island. Made measurements of stars and planets with unprecedented accuracy. Repeated measurements with different instruments to assess errors - pioneer of our modern practices. Tycho Brahe (1546 - 1601) • Attempted to test Copernicus’s ideas about the planets orbiting the Sun. • Failed to measure any stellar parallax; concluded Earth was stationary and Copernicus wrong. (We now know the stars were too far away to measure parallax without a telescope) • Compiled a massive data base with 1 = 1 arcmin accuracy (best one can do without a telescope) Tycho Brahe (1546 - 1601) • Attempted to test Copernicus’s ideas about the planets orbiting the Sun. • Failed to measure any stellar parallax; concluded Earth was stationary and Copernicus wrong. (We now know the stars were too far away to measure parallax without a telescope) • Compiled a massive data base with 1 = 1 arcmin accuracy (best one can do without a telescope) Johannes Kepler (1571 - 1630) Employed by Tycho in 1600 in Prague. After Tycho’s death Kepler inherited his data and his position as Imperial Mathematician of the Holy Roman Empire. Johannes Kepler (1571 - 1630) Employed by Tycho in 1600 in Prague. After Tycho’s death Kepler inherited his data and his position as Imperial Mathematician of the Holy Roman Empire. Johannes Kepler (1571 - 1630) Kepler could be said to be the first astrophysicist He could also be said to be the last scientific astrologer. (except maybe me) Johannes Kepler (1571 - 1630) Astrology was once kind of scientific Johannes Kepler (1571 - 1630) Astrology was once kind of scientific What happened last time Venus rose in the constellation of the goat? Maybe something like it will happen again. Johannes Kepler (1571 - 1630) Astrology Disaster: Johannes Kepler (1571 - 1630) Astrology Disaster: from the Greek for bad star Johannes Kepler (1571 - 1630) Astrology Disaster: from the Greek for bad star Influenza: Johannes Kepler (1571 - 1630) Astrology Disaster: from the Greek for bad star Influenza: the influence of the stars Johannes Kepler (1571 - 1630) Astrology Even today, how many papers have a regular astrology column? Johannes Kepler (1571 - 1630) Astrology Even today, how many papers have a regular astrology column? But how many have a regular astronomy column? Johannes Kepler (1571 - 1630) Astrology Based on the idea that the position of the planets in the sky fundamentally affect our lifes. But there are greater influences. Johannes Kepler (1571 - 1630) Kepler believed in the heliocentric model. 29 years of struggle with the data led him to try elliptical orbits with dramatic success. He confirmed this by mapping out the shape of orbits by observations with Earth’s orbit (1 AU) as baseline. Johannes Kepler (1571 - 1630) In Kepler’s time there were only 6 known planets: Mercury, Venus, Earth, Mars, Jupiter and Saturn. Johannes Kepler (1571 - 1630) In Kepler’s time there were only 6 known planets: Mercury, Venus, Earth, Mars, Jupiter and Saturn. Why not 20, or 100? Why these particular spacings? Before Kepler no one had asked such questions. Johannes Kepler (1571 - 1630) Consider an equilateral triangle, Draw a circle outside and one inside Johannes Kepler (1571 - 1630) Consider an equilateral triangle, Draw one circle outside, one inside and remove the triangle. Johannes Kepler (1571 - 1630) These two circles have the same ratio as did the orbit of Jupiter to the orbit of Saturn. Johannes Kepler (1571 - 1630) These two circles have the same ratio as did the orbit of Jupiter to the orbit of Saturn. Spooky eh! Johannes Kepler (1571 - 1630) These two circles have the same ratio as did the orbit of Jupiter to the orbit of Saturn. Spooky eh! But Kepler was intrigue and expanded on it. Johannes Kepler (1571 - 1630) These two circles have the same ratio as did the orbit of Jupiter to the orbit of Saturn. Spooky eh! But Kepler was intrigue and expanded on it. A triangular prism is a tetrahedron Johannes Kepler (1571 - 1630) These two circles have the same ratio as did the orbit of Jupiter to the orbit of Saturn. Spooky eh! But Kepler was intrigue and expanded on it. A triangular prism is a tetrahedron Johannes Kepler (1571 - 1630) Could a similar geometry relate the orbits of the other planets? Johannes Kepler (1571 - 1630) Could a similar geometry relate the orbits of the other planets? Kepler recalled the regular solids of Pythagoras. There were five. Johannes Kepler (1571 - 1630) Could a similar geometry relate the orbits of the other planets? Kepler recalled the regular solids of Pythagoras. There were five. Johannes Kepler (1571 - 1630) He believed they nested one within another. Hence the invisible supports of the 5 solids was the spheres of the 6 planets. Spheres enclosing solids Spheres enclosing solids Spheres enclosing solids All this, is an attempt to fit the orbits of the planets with harmonics in music. Johannes Kepler (1571 - 1630) But no matter how he tried, he could not make it work very well. Johannes Kepler (1571 - 1630) But no matter how he tried, he could not make it work very well. Why not? Johannes Kepler (1571 - 1630) But no matter how he tried, he could not make it work very well. Why not? Because it was wrong. Johannes Kepler (1571 - 1630) But no matter how he tried, he could not make it work very well. Why not? Because it was wrong. The later discovery of Uranus, Neptune, Pluto, and the others prove that Johannes Kepler (1571 - 1630) He spent 29 years trying to make it work, but in the end decided that it was the observations that were right, not his ideas. Hence, he finally abandoned them. Astronomy wins over astrology Johannes Kepler (1571 - 1630) In abandoning his regular solids, he was also able to free his mind of the perfect sphere/circle for orbital motion. Hence he considered that they may be elliptical. Drawing an Ellipse Johannes Kepler (1571 - 1630) Kepler’s 3 Laws of planetary motion: 1) Orbital paths of planets are ellipses, with the Sun at one focus.(1609) 2) Line joining the planet to the Sun sweeps out equal areas in equal times. 3) The square of a planet’s orbital period is proportional to the cube of its semimajor axis Kepler’s 1st Law • The orbit of every planet is an ellipse with the Sun at one focus. Planet P Sun at a focus Empty focus Kepler’s 1st Law r 1 e cos r and are polar coordinates e is the eccentricity of the ellipse is the semi-latus rectum Planet P Sun at a focus Empty focus Kepler’s 1st Law Planet rrP r and are polar coordinates Major axis Kepler’s 1st Law Eccentricity e a b a e 1 2 a b 2 Planet rrP Semi Major axis a Semi Minor Axis b 2 2 Kepler’s 1st Law Eccentricity e a b a e 1 2 a b 2 2 2 Kepler’s 1st Law Semi Latus Rectum Planet =b2/a rrP r 1 e cos Note that a circle is a special type is ellipse (one with e = 0) Kepler’s 2nd Law The line between the sun and a planet sweeps out equal areas in equal time. Kepler’s 2nd Law The line between the sun and a planet sweeps out equal areas in equal time. If the planet moves from A to B in one day. Then the Sun A and B roughly form a triangle. The area of that triangle is the same no matter where the planet is on its orbit. Kepler’s 2nd Law The orbit is an ellipse. Thus, the planet must move faster when near perihelion than it does near aphelion. Kepler’s 2nd Law The orbit is an ellipse. Thus, the planet must move faster when near perihelion than it does near aphelion. This is because the net tangential force involved in an elliptical orbit is zero. As the areal velocity is proportional to angular momentum, Kepler's second law is a statement of the law of conservation of angular momentum.. Kepler’s 2nd Law Written symbolically, d dt 1 2 r 0 2 1 2 r is the " areal velocity" 2 Kepler’s 3rd Law The square of the orbital period of a planet is proportional to the cube of its semi-major axis. P2 a3 Kepler’s 3rd Law The square of the orbital period of a planet is proportional to the cube of its semi-major axis. P2 a3 Example Uranus was found to have a period of 84 years. What is its distance from the Sun? Kepler’s 3rd Law The square of the orbital period of a planet is proportional to the cube of its semi-major axis. P2 a3 Example Uranus was found to have a period of 84 years. What is its distance from the Sun? a = P2/3 = 842/3 = 19 AU Using his laws Kepler was the first astronomer to predict a transit of Venus (for the year 1631) Galileo Galilei (1564 - 1642) One of the first to use a telescope From 1610 onwards he saw: mountains on the Moon, sunspots on the Sun, the rings of Saturn, Jupiter’s moons ( providing a counter example to the view that Earth is the centre of the universe) Galileo Galilei (1564 - 1642) One of the first to use a telescope, His observations constitute the beginnings of modern astronomy. His defence of the Copernican heliocentric solar system was published in The Starry Messenger. (Siderius Nuncius) Galileo Galilei (1564 - 1642) One of the first to use a telescope, His observations constitute the beginnings of modern astronomy. His defence of the Copernican heliocentric solar system was published in The Starry Messenger. (Siderius Nuncius) Galileo Galilei (1564 - 1642) He noted that as the phases of Venus changed, so did its apparent size. This provided decisive evidence against Ptolemaic geocentric system. Phases of Venus as it orbits a = angular diameter (arcsec) Venus in the Heliocentric system Venus in the Geocentric system Galileo Galilei (1564 - 1642) 1610: Using his telescope he discovered 4 moons orbiting Jupiter (the Galilean satellites) This provided a counterexample to the view that Earth is the centre of the universe Jupiter’s moons Jupiter’s moons 1610 Galileo observed Jupiter’s moons. Isaac Newton (1642 - 1727) One of the greatest scientists who ever lived: was a great experimentalist, mathematician, & philosopher of the scientific method . Isaac Newton (1642 - 1727) One of the greatest scientists who ever lived: was a great experimentalist, mathematician, & philosopher of the scientific method . Isaac Newton (1642 - 1727) Principia Mathematica 1667 Newton’s Laws of Motion: 1) A particle will continue moving in a straight line unless acted on by a force. 2) Application of a force, F causes an acceleration, a, given by ma = F 3) Action & reaction are equal and opposite. Isaac Newton (1642 - 1727) Principia 1667 Newton’s derivation of Centripetal Acceleration for motion in a circle using: 1) A particle will continue moving in a straight line unless acted on by a force. 2) Application of a force, F causes an acceleration, a, given by ma = F Centripental Position Velocity Centripental Position Draw a position vector Velocity Centripental Position Velocity Draw a position vector r Centripental Position Velocity Draw a position vector v r Centripental Position Velocity Draw a position vector Draw that velocity vector v r Centripental Position Velocity Draw a position vector Draw that velocity vector v r Centripental Position Velocity Draw that velocity vector v r Draw a position vector some time dt later Centripental Position Velocity Draw that velocity vector r v r Draw a radius vector some time dt later Centripental Position Velocity v r v r Draw a position vector some time dt later Centripental Position Velocity v r v r Draw a position vector some time dt later Draw that new velocity vector Centripental Position Velocity v r v r Draw a position vector some time dt later Draw that new velocity vector Centripental Position Velocity v r v r Now draw an acceleration vector Centripental Position Velocity v r v r Now draw an acceleration vector Centripental Position Velocity v r v r And here Now draw an acceleration vector Centripental Position Velocity v r v r Centripental Position Velocity v r v r The time taken for both the position vector and the velocity vector to complete one cycle must be the same. How long does it take the position to complete one cycle? v r v r How long does it take the position to complete one cycle? Circumference divided by the velocity. v r v r How long does it take the position to complete one cycle? Circumference divided by the thing that is changing: v. 2r P v v r v r How long does it take the velocity to complete one cycle? 2r P v v r v r How long does it take the velocity to complete one cycle? The circumference divided by the thing that is changing: a 2r P v v r v r How long does it take the velocity to complete one cycle? The circumference divided by the thing that is changing: a 2r P v 2v P a v r v r But the periods P are the same for both. 2r P v 2v P a v r v r But the periods P are the same for both. Hence, 2r 2v v a v r v r But the periods P are the same for both. Hence, 2r 2v v a v a r 2 v r v r Centripetal Acceleration v v dx dt dx vdt d dx r vdt d r dx r d r v’ Centripetal Acceleration vdt d r d dv dv v vdt v r dv v 2 dt r v v at A d v’ dv v at B Apply Newton’s 2nd Law 2 v F ma m r Apply Newton’s 2nd Law 2 v F ma m r v r F m r 2 Isaac Newton (1642 - 1727) Principia Mathematica 1667 Newton’s Laws of Motion: 1) A particle will continue moving in a straight line unless acted on by a force. 2) Application of a force, F causes an acceleration, a, given by ma=F 3) Action & reaction are equal and opposite. Isaac Newton (1642 - 1727) Principia 1667 Newton’s Law of Universal Gravitation Newton’s Law of Universal Gravitation mP r MSun Newton’s Law of Universal Gravitation mP r MSun F= G M S un m P r 2 Newton’s Law of Universal Gravitation mP r MSun F= G M S un m P r 2 Newton’s Law of Universal Gravitation m P How did Newton derive this law? r MSun F= G M S un m P r 2 Newton’s Law of Universal Gravitation m P He made it up r MSun F= G M S un m P r 2 Newton’s Law of Universal Gravitation m P Its an educated guess r MSun F= G M S un m P r 2 Newton’s Law of Universal Gravitation m P He made a few educated guesses r Until he found one that worked. MSun F= G M S un m P r 2 Isaac Newton (1642 - 1727) To keep the planet in an orbit of radius r, requires a centripetal force F(centripetal). This is provided by the Sun’s gravitational force F(grav). F(centripetal) = F(grav) Using the astronomer’s notation, r = a = semi-major axis Notice that this law applies to all planets, asteroids etc orbiting the sun. 4π 2 2 3 P = a G M sun P = period a = semi-major axis MSun= Solar mass ( M⊙) Notice that this law applies to all objects orbiting the sun. P 2 4 2 3 a GM Sun Earth has P = 1 yr, a = 1 AU 2 3 P (yrs) = a (AU) Kepler’s 2nd Law Kepler’s 2nd Law The line joining a planet to the sun sweeps out equal areas in equal time. A consequence of the law of conservation of momentum The ice skater Conserves Angular Momentum Angular Momentum is L = Momentum lever arm Illustrate for circular motion: L = mvr = mr Conservation is L = constant r 2 v m v r A r Area swept out on one second is: A r 2 P v r A r Area swept out on one second is: but P = 2p/w A r 2 P v r A r Area swept out on one second is: but P = 2/ r 2 r 2 A P 2 v r A r Area swept out on one second is: but P = 2/ and v = r r 2 r 2 A P 2 v r A r Area swept out on one second is: but P = 2/ and v = r r 2 r 2 vr A P 2 2 v r A r Conservation of Momentum L mvr constant Conservation of Momentum L mvr constant vr A 2 Conservation of Momentum L mvr constant vr L A 2 2m Conservation of Momentum L mvr constant vr L A 2 2m L, 2, and m are all constant, hence A must be a constant. Real Planetary Orbits Both bodies orbit about a common centre of mass. MASSES Real Planetary Orbits 1:1 Both bodies orbit 1:2 about a 1000:1 common centre of mass. SUN:Jupiter reflex motion of SUN 12.4 m/s Real Planetary Orbits rd Kepler's 3 Law (Newton's Form) 3 4π a P = GM 1 + M 2 2 2 Earth’s Moon 27.32 days 0.055 5.14 Example • Jupiter’s moon Europa has a period of 3.55 days and its average distance from the planet is 671,000 km. Determine the mass of Jupiter. 4a m J mE 2 GP 3 4a m J mE 2 GP 3 We know 4, , a, G, and P; but neither of the two masses, giving one equation with two unknowns. 4a m J mE 2 GP 3 We know 4, , a, G, and P; but neither of the two masses, giving one equation with two unknowns. 4a m J mE 2 GP 3 We know 4, , a, G, and P; but neither of the two masses, giving one equation with two unknowns. Make the reasonable assumption that the mass of Europa is zero. 4a m J mE 2 GP 3 We know 4, , a, G, and P; but neither of the two masses, giving one equation with two unknowns. Make the reasonable assumption that the mass of Europa is zero (i.e., that mJ + mE = mJ). 4a mJ 2 GP 3 4 6.7110 27 mJ 1.9 10 kg 2 11 6.67 10 3.55 86400 8 3 In Solar Units a in AU P in years M in solar masses 3 a M≈ P2 a E u r op a = 6 7 1× 1 0 6 /1 .4 9 6× 1 0 1 1 = 4 .4 9× 1 0 -3 A U P E u rop a = 3 .5 5 /3 6 5 .2 5 = 9 .7 × 1 0 -3 y e ars -3 M Ju p it e r = 0.9 6 2 × 1 0 M S u n THE END OF LECTURES 46