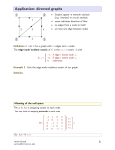
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Homework - BetsyMcCall.net
Euclidean vector wikipedia , lookup
Determinant wikipedia , lookup
Tensor operator wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Jordan normal form wikipedia , lookup
Perron–Frobenius theorem wikipedia , lookup
Vector space wikipedia , lookup
Non-negative matrix factorization wikipedia , lookup
Eigenvalues and eigenvectors wikipedia , lookup
Orthogonal matrix wikipedia , lookup
Singular-value decomposition wikipedia , lookup
Cayley–Hamilton theorem wikipedia , lookup
Covariance and contravariance of vectors wikipedia , lookup
Cartesian tensor wikipedia , lookup
Matrix multiplication wikipedia , lookup
Bra–ket notation wikipedia , lookup
System of linear equations wikipedia , lookup
Linear algebra wikipedia , lookup
Matrix calculus wikipedia , lookup
MAT 202, Homework #5, Summer 2016 Name _______________________________________________
Instructions: Write your work up neatly and attach to this page. Use exact values unless specifically
asked to round. Show all work.
1. For each statement below determine if it is true or false. If the statement is false, briefly explain
why it is false and give the true statement. Assume B is a basis for the vector space V.
a. Asking whether b is in the span a1 , a2 , a3 is the same thing as asking whether the linear
system corresponding to an augmented matrix a1
a2
a3 b has a solution.
b. The equation Ax b is referred to as a vector equation.
c. The equation Ax b is consistent if the augmented matrix A b has a pivot in every
row.
d. If the columns of an mxn matrix A span 𝑅 𝑛 , then the equation Ax b is consistent for each
b in 𝑅 𝑚 .
e. The homogeneous equation Ax 0 has the trivial solution if and only if the equation has a
least one free variable.
f.
The equation x p tv describes a line through v parallel to p .
g. If Ax b is consistent, then the solution of Ax b is obtained by translating the solution
set of Ax 0 .
h. A single vector by itself is linearly independent.
i.
If H span b1 ,..., bn , then b1 ,..., bn is a basis for H.
j.
The columns of an invertible nxn matrix form a basis for R n .
k. The basis is a spanning set that is as large as possible.
l.
In some cases, the linear independence relations among the columns of a matrix can be
affected by certain elementary row operations of the matrix.
m. A linearly independent set in a subspace H is a basis for H.
n. If a finite set S of nonzero vectors spans a vector space V, then some subset of S is a basis for
V.
o. The null space of A is the solution set of the equation Ax 0 .
p. The null space of an mxn matrix is in 𝑅 𝑚 .
q. The kernel of a linear transformation is a vector space.
r.
A null space is a vector space.
s. Col A is the set of all solutions of Ax b .
t.
The standard method for producing a spanning set for Nul A, described previously,
sometimes fails to produce a basis for Nul A.
u. If B is an echelon form of a matrix A, then the pivot columns of B for a basis for Col A.
v. If x is in V and if B contains n vectors, then the B -coordinate vector of x is in R n .
w. The vector space P3 and R 3 are isomorphic.
x. If B is the standard basis for R n , then the B -coordinate vector of an x in R n is x itself.
y. In some cases, a plane in R 3 can be isomorphic to R 2 .
z. The row space of A is the same as the column space of AT.
aa. The sum of the dimensions of the row space and the null space of A equals the number of
rows of A.
bb. The dimensions of the null space of A is the number of columns of A that are not pivot
columns.
cc. If A and B are row equivalent, then their row spaces are the same.
dd. Dim Row A + dim Nul A = n
ee. If the equation Ax 0 has only the trivial solution, then A is row equivalent to the nxn
identity matrix.
ff. If the columns of A are linearly independent then the columns of A span 𝑅 𝑛 .
gg. If there is a b in 𝑅 𝑛 such that the equation Ax b is consistent, then the solution is
unique.
hh. If PB is the change-of-coordinates matrix, then x PB x for x in V.
B
ii. The columns of the change-of-coordinate matrix P are B-coordinate vectors of the
CB
vectors in C.
jj. The columns of P are linearly independent.
CB
2. Describe the possible echelon forms of the matrices below using 0, 1 for the pivot and * for all
other entries.
a. A is a 2x2 matrix with linearly independent columns.
b. A is a 4x3 matrix, A a1
a2
a3 , such that a1 , a2 is linearly independent and a3 is
not in span a1 , a2 .
c. How many pivot columns must a 6x4 matrix have if its columns are independent? Why?
1
4
3
0
3. List 5 vectors in the span of
and .
2
1
0
1
4. Determine if the columns of each matrix spans 𝑅 4.
4
3
a.
5
9
5
7
b.
11
3
5
7
6
1
11
3
5
4
1
4
1
10
6
4
6
7
8
2
4
7
7 12
6 9
9 3
2 7
5. For each of the sets of bases for R 3 , determine which ones are linearly independent and which
ones span R 3 .
1 1 1
a. 0 , 1 , 1
0 0 1
2 2 8
b. 1 , 3 , 5
1 2 4
1 4
c. 2 , 3
4 6
1 0 2 0
d. 2 , 3 , 1 , 0
3 1 5 1
6. Find a basis for the space spanned by the given vectors.
1 0 2 2 3
0 1 2 1 1
a. , , , ,
2 2 8 10 6
3 3 0 3 9
3 3 0 6 6
2 0 2 2 3
b. 6 , 9 , 4 , 14 , 0
0 0 0 0 1
7 6 1 13 0
7. Find vectors that span the null space of the following matrices.
1
0
1
b. 0
0
a.
0
1 3 2
2 4
3 4 3 1
1 3 1 0
0 0 0 0
8. Answer the following questions, and then explain why you know this to be the case. State a
theorem or definition that applies.
a. If a 7x5 matrix A has rank 2, find dim Nul A, dim Row A, and rank AT.
b. Suppose a 6x8 matrix A has 4 pivot columns. What is dim Nul A? Is Col A = R 4 ? Why or
why not?
c. If the null space of an 8x7 matrix is 5-dimensional, what is the dimension of the Col space of
A?
d. If A is a 5x4 matrix, what is the largest possible dimension of the row space of A?
e. If A is a 7x5 matrix, what is the smallest possible dimension of Nul A?
f.
Suppose the solutions of a homogeneous system of 5 linear equations in 6 unknowns are all
multiples of one nonzero solution. Will the system necessarily have a solution for every
possible choice of constants on the right sides of the equations? Explain.
9. Find a basis for the subspace and state the dimension.
p 2q
2 p 5r
a.
: p, q, r R
2q 2r
3
p
6
r
1 3 2 3
b. 2 , 6 , 3 , 5
0 0 5 5
3 2 6 0
1 0 3 7
c.
, for Col A and Nul A.
0 1 4 2
0 0 0 1
d. {1,1 t , 2 4t t 2 ,6 18t 9t 2 t 3}
1
0
0
0
2 4
0 0
0 0
0 0
1 1 2 4 1 2
1
1 2 3 0 2 3
0
10. If A 1 1 0
0
1
6 is row equivalent to B 0
1 3 0
1 2 2
0
1 2 1 4 2 1
0
1 2 4
1 1
0 1
0
1
0
0
0
0
0
0
2
3 1
13 1 ,
1
1
0
1
1
find a basis for Col A, Row A and Nul A. Find rank A and dim Nul A without calculations.
11. Given the bases B and C, and the given vector in one the bases, find the coordinate vector in the
other basis.
−4
1
0 3
1 2 2
a. B= {[2] , [1] , [2]}, C= {[−1] , [1] , [4]}, [𝑥⃗]𝐶 = [ 10 ]
4 3 1
2
1 5
11 𝐶
2
0
2 1
5
2
1
1
5
b. B= {[−2] , [1] , [2] , [0]}, C= {[2] , [ 1 ] , [0] , [0]}, [𝑥⃗]𝐵 = [ 2 ]
2
0 −1 1 0
2 1 3
−3
−1 1 0 1
3
1
0 4
10 𝐵

















![§1.8 Introduction to Linear Transformations Let A = [a 1 a2 an] be](http://s1.studyres.com/store/data/006151798_1-1596c7f77f21452ed436a495dc65f749-150x150.png)