* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Ratio
Survey
Document related concepts
List of important publications in mathematics wikipedia , lookup
Philosophy of mathematics wikipedia , lookup
History of mathematics wikipedia , lookup
Mathematics wikipedia , lookup
Critical mathematics pedagogy wikipedia , lookup
Foundations of mathematics wikipedia , lookup
Secondary School Mathematics Curriculum Improvement Study wikipedia , lookup
Mathematics and art wikipedia , lookup
Ethnomathematics wikipedia , lookup
Mathematics and architecture wikipedia , lookup
List of works designed with the golden ratio wikipedia , lookup
Transcript
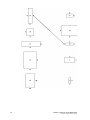
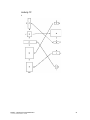
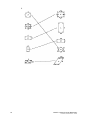
Ratios Ratio 3 What is a ratio? 3 Simplifying ratios 4 Ratios 7 Equivalent ratios 9 Problems involving ratio 11 Dividing a quantity in a given ratio 13 Similar figures 17 Suggested responses to activities 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 22 1 2 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 Ratio What is a ratio? A ratio compares two or more quantities of the same kind in a special order. For example, if you have four red smarties and seven yellow smarties, then the ratio is written as: Red smarties:Yellow smarties = 4:7 Figure 1: Example of ratios We read this as ‘the ratio of red smarties to yellow smarties is 4 to 7’. The numbers 4 and 7 are called the terms of the ratio. Look at the following advertisement: Great bargains!! Melbourne—2 nights from just $259 Gold Coast—5 nights from just $319 Adelaide—2 nights from just $369 Cairns—5 nights from just $589 What is the cost ratio of the Melbourne trip compared to the Adelaide trip? The answer is 259:369. If we wrote 369:259, it would be wrong, as this would be the Adelaide cost compared to the Melbourne price. 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 3 The order of the numbers in a ratio is very important. Simplifying ratios Now let’s look at simplifying ratios. We usually simplify ratios in the same way that we simplify fractions. In comparing two quantities we often do not know the actual size of either. For example, Kate says she has ‘four times as much money as Bjorn.’ There are an infinite number of actual ratios that could describe this situation, such as: (a) $8: $2 (b) $20: $5 (c) $40: $10 (d) $120: $30 (e) 16c: 4c In all of these, the first term is four times the second term and the simplest ratio to express this is 4:1. In this way ratios can be simplified like equivalent fractions. That is: 1 2 Simplify: (a) 8:6 ________________ (b) 36:12 ______________ (c) 9:12:3 ______________ A fruit drink contains 50% pineapple juice, 20% orange juice and the rest is water. What is the ratio of: (a) Pineapple to orange juice? _________________________________ (b) Orange juice to water? ____________________________________ 4 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 1 2 (a) 8:6 = 4:3 (Divide both numbers by 2.) (b) 36:12 = 3:1 (Divide both numbers by 12, the highest factor of both.) 9:12:3 = 3:4:1 (Divide each number by 3.) P:O = 50:20 = 5:2 (Divide both number by 10.) (c) (a) (b) O:W = 20:30 = 2:3 (Divide both numbers by 10 noting that water must make up 30% of the juice giving a total of 100%.) Note: For large terms you may need to divide the numbers several times. For example, to simplify: A ratio is in its simplest form when its terms are whole numbers that have no common factors. Activity 7A Write the answers to the following problems in your workbook. 1 There are four blue-eyed people and one brown-eyed person in my family. Write down the ratio for blue-eyed people to brown-eyed people. 2 A university student has three mathematics texts, four English texts and two psychology texts. What is the ratio of: (a) Mathematics texts to English texts? (b) Psychology texts to mathematics texts? 3 A survey of traffic in the main street stated: ‘There are five trucks for every fourteen cars’. (a) What is the ratio of trucks to cars? (b) Does the statement mean that only five trucks and fourteen cars were counted? 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 5 4 A proportion is a statement that two or more ratios are equal. State whether these proportion statements are true or false: (a) 6:12 = 1:2 (b) 49:7 = 9:1 (c) 8:32 = 4:1 (d) 27:6 = 9:2 (e) 24:36 = 8:13 (f) 2:4:6 = 1:2:3 5 Write the following ratios in their simplest form: (a) 4:8 (b) 20:15 (c) 18:16 (d) 22:12 (e) 2.4:3.6 [Hint: multiply both terms by 10 then simplify.] (f) 15:10:100 (g) 200:40:80 6 Alec and Bertha invest $4200 and $2800 each in a business. What is the ratio of Alec’s share to Bertha’s share? Check your answers with the suggested responses at the end of the topic. 6 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 Ratios in real life It is important that you compare things of the same kind. For example, length must be compared with length, not with weight. In comparing things we usually make sure that they are measured in the same units. Figure 2: Length and weight Example 1 Simplify 18 kg:9 kg. The units are the same, so 18:9 = 2:1 Example 2 This example has different units. Change the hours to minutes. 2 ½ hours: 50 minutes = 150 minutes: 50 minutes = 3: 1 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 (Remember, there are 60 minutes in 1 hour and 30 minutes in ½ hour.) Remember, simplify by dividing. 7 Activity 7B Write the answers to the following problems in your workbook. Write the following ratios in their simplest form, after first changing to the same units. (a) 1 m:50 cm (There are 100 centimetres in 1 metre.) (b) 1 ½ hours:30 minutes (c) 2 days:6 hours (d) $1.50:70 cents (e) $14:$7.50 (f) 1 m:12 cm (g) 2 g:2 kg (There are 1000 grams in 1 kilogram.) (h) 5 cm:20 mm (There are 10 millimetres in 1 centimetre.) (i) 3 L:500 mL (There are 1000 millilitres in 1 litre.) (Remember, 24 hours in one day.) Check your answers with the suggested responses at the end of the topic. 8 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 Equivalent ratios As well as simplifying ratios, you can change them by multiplying the terms by the same number. Here’s an example. Find the missing term in this proportion statement: 8:5 = 24: Answer (Multiply both terms by 3, since 24 = 8 3) Therefore = 15 Another example From a box of smarties take out three orange smarties and two brown smarties. If you double the number of orange smarties to six, what would you have to do to keep the ratio of orange smarties to brown smarties the same? Answer Orange:brown = 3:2 3:2 = 6: (Multiply both terms by 2, since 6 = 3 × 2) So you would need four brown smarties to keep the ratio of orange smarties to brown smarties the same. 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 9 Activity 7C Write the answers to the following problems in your workbook. Complete the following ratios by filling in the blank squares: (a) 2:5 = 4: (b) 8:1 = 24: (c) 3:2 = :6 (d) 3:4 = :40 (e) 2:7 = 12: (f) 6:5 = 30: (g) 9:36 = 36: (h) 1:4 = :12 (i) 2:3:4 = :15: Check your answers with the suggested responses at the end of the topic. 10 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 Problems involving ratio In the first type of ratio problem we will look at, we are told the ratio of two quantities. We are then given one quantity and asked to find the other. Examples 1 In a group of people, the ratio of people with brown eyes to blue eyes is 5:3. If there are 21 blue-eyed people, how many brown-eyed people are there? 2 In a tennis club the ratio of men to women is 4:7. If there are 32 men, how many women are there? Answers 1 Brown:blue = 5:3 That is, 5:3 = :21 (Multiply both terms by 7, since 21 = 3 × 7) So there are 35 brown-eyed people. 2 (Multiply both terms by 8, since 32 = 4 × 8) So there are 56 women in the club. 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 11 Activity 7D Write the answers to the following problems in your workbook. 1 The ratio of adults to children watching a soccer game is 10:3. If there are 60 adults how many children are there? 2 Daniel and Tracey divide some money in the ratio 2:3. If Tracey has $2.70 how much does Daniel have? 3 A mortar mix is made up of sand and cement in the ratio 4: 1. If 12 buckets of sand is used how much cement is needed? 4 The ratio of a boy’s weight to that of his father is 3:7. If the boy weighs 33 kg, how much does his father weigh? 5 The ratio of teachers to students in a TAFE college is 1:15. In a college of 960 students, how many teachers are there? 6 A type of solder is made by mixing lead and tin in the ratio 2:3. How much lead would be needed to be mixed with 150 g of tin? 7 At a college the ratio of female students to male students is 5:4. If there are 420 male students, find: (a) the number of female students (b) the total enrolment of the College. 8 A sum of money is divided between three friends in the ratio 8:3:5. If the smaller share is $15, what are the other shares and how much was there to be divided? Check your answers with the suggested responses at the end of the topic. 12 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 Dividing a quantity in a given ratio The second type of ratio problem involves dividing or sharing a quantity in a given ratio. In this case the total quantity is known. Examples 1 Ahmed and Belinda do some odd jobs for their neighbour, who pays them $40. If Ahmed works for two hours and Belinda works for three hours find: (a) the ratio of Ahmed’s hours to Belinda’s hours ______________________________________________________ (b) what fraction of the total hours did: (i) Ahmed work? ______________________________________ (ii) Belinda work? ______________________________________ (c) How much should each get? ______________________________________________________ ______________________________________________________ 2 3 In a town the ratio of adults to children is 2: 5. If there are 9100 people in the town how many children are there? A dough mix is made by mixing flour, water and salt in the ratio 10:9:1. How much of each ingredient is needed to make 400 g of dough? 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 13 Answers 1 (a) 2:3 (b) (i) (Note: total hours = 2 + 3 = 5) (ii) (c) Ahmed worked for of the time so should get Belinda worked for of the time so should get of 40. of 40. Therefore: 2 Ahmed should get × 40 = $16 Belinda should get × 40 = $24. The total population is 9100. Adults:children = 2:5 Note: There is no need to find the number of adults as the question only asks for the number of children. 3 14 Flour is of the mix. Water is of the mix. 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 Salt is of the mix. Activity 7E Write the answers to the following problems in your workbook. 1 A class contains 14 boys and 16 girls. (a) What is the ratio of boys to girls? (b) What is the ratio of boys to the total number of students in the class? (c) What fraction of the class are boys? (d) What fraction of the class are girls? 2 Concrete is made by mixing cement, sand and gravel in the ratio 1:3:4. (a) What fraction of concrete is cement? (b) What fraction of concrete is gravel? (c) How much gravel is needed to make 64 kg of concrete? 3 Share these amounts in the ratio given: (a) 15 pens in the ratio 1:2 (b) $60 in the ratio 3:2 (c) 420 kg in the ratio 3:4 (d) $2.50 in the ratio 8:2. 4 A chemical solution is made by mixing an acid with water in the ratio 1:24. How much acid is needed for a 200 mL solution? 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 15 5 Company A and Company B wish to invest in the following business opportunity in the ratio 5:6. How much money does each company need to put into the deal? NOWRA REAL ESTATE $88 000 o.n.o. 2 fabulous commercial strata suites. Suit professional or small business Prime position. BARGAIN. 6 Frank and Nigel pooled their savings to start up a lawn mowing business. Frank invested $6000 while Nigel invested $4000. (a) Find the ratio of their investments, in simplest form. (b) In their first month of trading they made a profit of $270. How much should each receive, if this is divided up in the ratio of their investments? 7 Sarah and Rebecca contributed $7 and $3 (respectively) to buy a $10 raffle ticket which had a $25 000 first prize. They won! How much should each receive? 8 A bread mixture is made by mixing flour, water and honey in the ratio 6:3:1. What quantity of each ingredient is needed to make a 450 g loaf? 9 A recipe for a punch requires fruit juice and soft drink to be mixed in the ratio 5:3. To make 10 litres of punch, (a) how much fruit juice is needed? (b) how many 1.25 L bottles of soft drink will need to be purchased? 10 A metal alloy is made by mixing copper and nickel in the ratio 7:5. What mass of each metal is contained in a 6 kg block of the alloy? Check your answers with the suggested responses at the end of the topic. 16 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 Similar figures When we enlarge a photograph, the enlargement is the same shape as the original photo. We say that the enlargement and the original are similar figures. Two figures are similar if they have the same shape. 1 (a) A photograph is 15 cm long and 9 cm wide. If the photograph is to be enlarged so that the length is 30 cm, what will the width be? ___________________________ (b) (c) 2 A photograph is enlarged. If the length is tripled, what happens to its width? ___________________________ When a photograph is enlarged is it possible to increase the length without changing the width? ___________________________ The two rectangles shown are similar. What is the ratio of: (a) the lengths ____________ (b) the widths ____________ 1 (a) 18 cm. 2 (b) (c) (a) It is tripled. No. 8:16 = 1:2 (b) 3:6 = 1:2 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 17 In similar figures all matching angles are equal and all matching sides are in the same ratio. Example The diagram shows two figures with equal angles marked by the same symbol. (a) What is the ratio of corresponding (matching) sides? (b) Are the figures similar? Answer (a) (b) Since matching angles are equal and matching sides are in the same ratio the figures are similar. 18 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 Activity 7F Write the answers to the following problems in your workbook. 1 By checking ratios of matching sides, join each pair of similar rectangles. The first has been done for you. 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 19 20 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 2 After checking that matching angles are equal and that their matching sides are in the same ratio, join each pair of similar figures. Check your answers with the suggested responses at the end of the topic. 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 21 Suggested responses to activities Activity 7A 1 4:1 2 (a) 3:4 3 4 (b) 2:3 (a) 5:14 (b) No. The simplified ratio is 5:14. There may have been 10 trucks and 28 cars, or 50 trucks and 140 cars etc. (a) T (b) (c) (d) (e) F F T F 5 (f) T (a) 1:2 6 (b) 4:3 (c) 9:8 (d) 11:6 (e) 2:3 (f) 3:2:20 (g) 5:1:2 4200:2800 = 3:2. Activity 7B (a) 2:1 (b) 3:1 (c) 8:1 (d) 15:7 (e) 28:15 (f) 25:3 22 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 (g) 1:1000 (h) 5:2 (i) 6:1 Activity 7C (a) 10 (b) 3 (c) 9 (d) 30 (e) 42 (f) 25 (g) 144 (h) 3 (i) 10, 20. Activity 7D 1 18 children 2 $1.80 3 Three buckets of cement. 4 77 kg 5 64 teachers 6 100 g of lead 7 (a) 525 female students (b) 945 students altogether. Other shares: $40 and $25. Total = 40 + 15 + 25 = $80. 8 Activity 7E 1 (a) 14:16 = 7:8 (b) 14:30 = 7:15 (c) (d) 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 23 2 (a) (b) 4 (c) 32 kg of gravel. (a) 5 Pens:10 Pens (b) $36:$24 (c) 180 kg:240 kg (d) $2:$0.50. 8 mL of acid. 5 $40 000 (A) and $48 000 (B) 6 7 (a) 3:2 (b) $162 (Frank) and $108 (Nigel) $17 500 (Sarah) and $7500 (Rebecca) 8 270 g (flour), 135 g (water), 45 g (honey) 9 (a) 3 (b) 3 Bottles of soft drinks (to make 24 of soft drinks) 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 Activity 7F 1 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996 25 2 26 4930CF: 7 Applying Everyday Mathematics DET NSW, 2005/008/012/06/2006 P0025996