Download Meas_chap4-edit

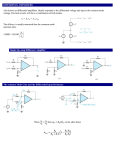
Basic Electrical Measurements and
Sensing Devices


Many measuring devices depend on some basic
electrical principal for their operation. Also, nearly all
data gathering and analysis systems depend on
electronic devices.
Hence, it is crucial to discuss some electrical devices
currently used to emphasize their use in the
measurement process.
Forces of Electromagnetic Origin

If a charge moves through a
conductor which exists in a
magnetic field, a force (F)
exerted on the conductor as
a result of the interaction
between the charge and the
magnetic field.
i
B
F
Forces of Electromagnetic Origin


This force can be written as:
F = BiL
where:
B: magnetic field density, in tesla (Weber/meter square)
i : the current in the conductor
L: the length of the conductor
This equation is very important… It provides a bridge
between a basic electrical quantity (i) and a mechanical
property (F). It reduces the problem of measuring i into
simply measuring F.
Forces of Electromagnetic Origin

Consider the accompanying
figure. As i flows through the
conductor, the spring will
stretch and develop the force
required to balance the
electromagnetic force. By
equating the two forces:
Kx = Bil
i can be found as:
i = (K/BL) x
where K is the spring constant
Fs = Kx
i
F = Bil
B
Basic Analog Meters

In order to extend the previous concept into a more
realistic model of actual current-measuring meters,
we use a coil instead of a single-wire conductor. If
the coil has N turns, then the exerted force can be
given by:
F = NBiL
Basic Analog Meters



The D’ Arsonval movement may be used only for the
measurement of direct current (dc).
Two different types of movements are used for
alternating current (ac) measurement; the iron-vane
or moving-iron, and electrodynamometer.
In the iron-vane instrument, the current is applied to
a fixed coil. The iron vane is movable and connected
to a restraining spring. The displacement of the vane
is then proportional to the inductive force exerted by
the coil.
Basic Analog Meters



In order to measure a dc voltage, a voltmeter may be
easily constructed by placed a resistor in series with a
current meter. Thus, when the instrument is
connected to a voltage source, the current in the
instrument is an indication of the voltage.
A series-resistor arrangement may also be used with
the iron-vane.
Study the electrostatic-voltmeter…(page 156).
Basic Input Circuits

The general method of gathering, processing, and displaying
physical information includes the following steps:
1) Transducer: converts the physical property into an electrical
signal. E.g.: microphone, thermocouple, solar cell…
2) Input circuit.
3) Signal conditioning: for noise reduction.
4) Transmission.
5) Processing: E.g.: AM radio receiver
6) Display: E.g.: cathode-ray screen, flash memory disks,…
Basic Input Circuits
Physical
Signal
Transducer
Input circuit
Property
Display
Signal
Conditioning
Processing
Transmission
Basic Input Circuits

Consider a gas sensor resistance of which changes as a
function of the gas concentration surrounding the sensor.

The following figure represents a simple type of input
circuit which uses the current flow through the sensor
resistance as an indication of the value of the resistance.

The current is given as:
i = E/(R +Ri)
Basic Input Circuits
Ri
i
Ei
Rm
R
Basic Input Circuits-Balanced Bridges



Bridge circuits are used to measure resistances, inductances,
and capacitances.
These bridges can be broadly classified into: balanced and
unbalanced.
The Wheatstone bridge is normally used for measuring
resistances in the range of 1 to 1M, (see figure 4.24.)
Basic Input Circuits-Balanced Bridges

The Wheatstone bridge is widely used for measuring the
output resistance of various transducers, such as resistance
thermometers, strain gages, and other devices that register
the change in the physical variable as a change in output
resistance.

R2 and R3 are normally known. R1 is a variable resistance,
and Rx is the unknown resistance associated with the
transducer output.
Basic Input Circuits-Balanced Bridges


The voltage E is applied to the
bridge.
The bridge may be balanced by
adjusting R1 until the sensing
device (G) indicates no current
flow. When this occurs, the
voltage drop across R2 must be
equal the voltage drop across R1
since this implies the difference
between B and D must be zero.
In this case:
Basic Input Circuits-Balanced Bridges
EB = ED, or:
i2R2 = i1R1
Also at balance:
i2 = i3 = E/(R2 +R3), and:
i1 = ix = E/(R1 +Rx),
By eliminating the currents from these relations, the result is:
Rx = R1R3/R2
Hence, Rx can be found in terms of the other three resistances.
Basic Input Circuits-Unbalanced
Bridges



If the galvanometer does not have a null reading, we say
that the bridge is unbalanced.
Unbalanced bridges are particularly important for the
measurements of dynamic signals where insufficient time is
available for achieving balance conditions.
Consider the bridge circuit shown in figure 4.25. Rg is the
galvanometer resistance; ib and ig are the battery and
galvanometer currents, respectively. Rb represents the
resistance of the power supply.R4 is the unknown resistance
Basic Input Circuits-Unbalanced
Bridges



If the bridge is slightly unbalanced, Rb effect can be
eliminated and ig can be written as:
ig = Eg/(R+Rg) ,
where R is the effective resistance of the bridge circuit
presented to the galvanometer and is given by:
R = R1R4/(R1+R4) + R2R3/(R2+R3)
The voltage presented at the terminals of the galvanometer
Eg is:
Eg = E[(R1/(R1+R4)-R2/(R2+R3)]
Finally, substitute in the ig equation and solve for R4.
Amplifiers

In many experimental measurements the signals are
comparatively weak and must be amplified before they
can be used to “drive” an output device. Typical situations
where amplifiers are used is the sound systems.

Consider the given amplifier schematic below. Without
the feedback-attenuator loop, the amplifier gain (A) is
given as:
A = Eo/Ei
Amplifiers
E=Ei - Ef
Ei
Amplifier
Gain = A
Ef=KEo
Attenuator, K
Eo
Amplifiers

Now, the feedback system attenuates Eo by a factor k and
feeds it back into the input. The feedback voltage is Ef =
KEo, is subtracted from Ei resulting in an input to the
amplifier of E = Ei-Ef. Now the gain of the amplifier with
the feedback system is:
Af = Eo/Ei = Eo/[(Eo/A) + kEo] = A/(1+Ak)

If Ak is very large,
Af  1/k
Amplifiers

A differential amplifier is a device which provides for two
inputs and an output proportional to the difference in the
two input voltages. Generally, it has a gain of:
A = Eo/abs(Ei,1 – Ei,2)
Ei,2
A
Ei,1
Eo
Transformers


Transformers are used to match impedance in many
experimental situations.
An ideal n-turn transformer is shown below
+
i2
n:1
i1
+
v2
v1
-
-
Transformers

For this transformer:
v2 = nv1
i2 = (1/n)i1,
therefore:
v2
v
 n2 1
i2
i1

Also, We may state that the output impedance Z2 is related
to the input impedance Z1 by:
Z 2  n Z1
2
Signal Conditioning



Noise can be defined as the unwanted part of a
signal. It is present in all physical situations in which
measurements are attempted.
A priori knowledge of frequencies ranges in which the
desired signal exits can significantly help the
experimenter.
For example, the human ear responds only to signals
in the range of frequencies between 20 Hz and 18
kHz. Therefore, the processing of a sensor used for
such sounds can consider all frequencies out of this
range as noise.
Signal Conditioning


Filters operate such that they allow only for a certain
range of frequencies to pass through it.
Various arrangements may be used for filter circuits,
but they fall into three categories:
1)lowpass: permits the transmission of signals with
frequencies below a certain cut off value,
2)highpass: permits the transmission of signals with
frequencies above a certain cut off value,
3)banpass circuits: permits the transmission of signals
with frequencies in a certain range.
Signal Conditioning


Gain is a dimensionless quantity, but engineers speak
of decibels of gain or loss as:
Decibels = 10logP2/P1
Decibels = 20logE2/E1
Decibels = 20logI2/I1
where P2/E2/I2 and P1/E1/I1 are the input and output
powers/voltage/current, respectively.
When the ratio of P2/P1 less than 1, the gain in
decibels is negative. For such circuits, insertion loss is
defined as: 10logP1/P2
Signal Conditioning

E.g.: calculate the overall voltage amplification for:
Gain
1000
Eo = 1mV
Gain
25
E1 = 1V
Sol. 20logE2/E0 = 87.92dB
E2 = 25V
Signal Conditioning

A simple RC circuit is to be used as a lowpass filter. It
is desired that the output voltage be attenuated 3 dB
at 100Hz. Calculate the required time constant
(T=RC) value?
Eo/Ei = -3
or: -3= 20logE2/E1
Thus: Eo/Ei = 0.708
= 1/(1+2T2)1/2
where: 2= (2f)2=[2(100)]2
So: T = 0.00159s. That is, the circuit can be built using
a 1.0F capacitor and 1.59k resistor
The Differential Transducer



See figure 4.48.
This is a distance-measuring transducer
Working method:
- An ac voltage is impressed in the primary coil
- the output voltage from the two secondary coils
depends on the magnetic coupling between the core
and the coils.
- this coupling is dependent on the position of the core.
- thus, the output voltage is a measurement of the
displacement of the core. That is, an Eo-displacement
calibration curve can be drawn for this device.
Capacitate Transducer


See figure 4.52
The capacitance (in picofarads) for this arrangement is
given by:
C = 0.0885A/d
where:
d : the distance between the plates, cm
A : overlapping area, cm2
 : dielectric constant (equals1 for air and 3 for plastics)
Capacitate Transducer

Working method:
- changing A, d, or  would result in a change in C.
- C may be measured with bridge circuit.
- this transducer can be used for displacement
measurement through changing in A or d.
- It is also used to measure liquid-levels by changing ,
(see figure 4.53).