* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 3.4: Parallel and Perpendicular Lines 3.5: Parallel Lines and Triangles
Survey
Document related concepts
Technical drawing wikipedia , lookup
Golden ratio wikipedia , lookup
Noether's theorem wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Euler angles wikipedia , lookup
Duality (projective geometry) wikipedia , lookup
Four color theorem wikipedia , lookup
Perspective (graphical) wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Line (geometry) wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Transcript
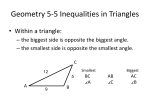
3.4: Parallel and Perpendicular Lines Theorem: If two lines are parallel to the same line, then they are parallel to each other. Theorem: In a plane, if two lines are perpendicular to the same transversal, then the two lines are parallel to each other. Theorem: In a plane, if a line is perpendicular to one of two parallel lines, then it is perpendicular to the other. a ll b and a t a b t 3.5: Parallel Lines and Triangles Triangle: A figure formed by three segments joining three noncollinear points. B Triangle ABC ( ABC) Vertices of C A Sides of Angles of Classify Triangles by the number of congruent sides Classify Triangles by their angles Auxiliary Line: A line added to a diagram to help in a proof. Triangle Sum Theorem Example: The sum of the measure of the angles of a triangle is 180. Find the value of x. Then give the measure of each angle. The measure of on angle of a triangle is 5 more than the measure of the smallest angle. The measure of the third angle is three times the measure of the smallest angle. What are the measures of the 3 angles? Use the given information to ind the unknown angle measures in the triangle. 100 53 12 w x 2x + y y 5x + y 5x The perimeter of my triangle is 60 ft. The sides are in the ratio 3:4:5. What are the sides of my triangle?