Download undergraduate celestial co

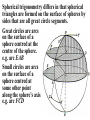
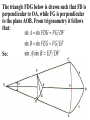
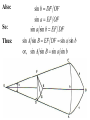
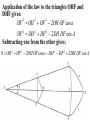
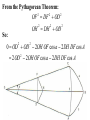
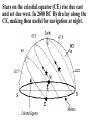
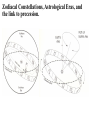
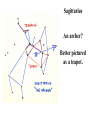
Astronomy 2100
Foundations of Astrophysics
(Astronomy Basics)
Examine directly observable quantities for
stars, such as their positions on the celestial
sphere and the light they emit. Topics
include properties of the celestial sphere,
time-keeping, astronomical catalogues, the
two-body problem, dynamics of star clusters,
emission and absorption lines in stellar
spectra, and the operation of telescopes.
Training in the use of the Burke-Gaffney
Observatory is done in conjunction with
assigned observing projects.
1. The Celestial Sphere
Goals:
1. Gain familiarity with the basic equations
of spherical astronomy and how they are
used for establishing astronomical coordinate systems.
2. Tackle problems in practical astronomy
involving timekeeping and star positions.
3. Introduce a bit of archeoastronomy, and
the origin of the constellations.
Spherical Astronomy:
Recall triangles in plane trigonometry.
A, B, and C denote
angles
a, b, and c denote
opposite sides
Interrelated through:
Spherical trigonometry differs in that spherical
triangles are formed on the surface of spheres by
sides that are all great circle segments.
Great circles are arcs
on the surface of a
sphere centred at the
centre of the sphere.
e.g. arc EAB
Small circles are arcs
on the surface of a
sphere centred at
some other point
along the sphere’s axis.
e.g. arc FCD
The triangle PAB is a spherical
triangle. The triangle PCD is
not, as illustrated, since the
side CD is a small circle. PCD
becomes a spherical triangle
if the points C and D are
connected by a great circle
rather than a small circle.
The triangle ABC at left is a
spherical triangle. Its sides a,
b, and c are angles like A, B,
and C, in this case the arc
lengths subtended by identical
angles a, b, and c at the centre
of the sphere, a = rsphere cos a =
cos a, when rsphere = 1.
By definition, no side of a spherical triangle can
exceed 180 = π radians. Angles in a spherical
triangle denote the angles between two planes
that form the sides of the triangle. The surface
area of a spherical triangle is denoted as Δ.
If θ is the angle between two
great circles on the surface of
a sphere, then the surface
area enclosed by the angle θ is
S(θ). If θ = π, then S(π) must
encompass the entire area of
the sphere, i.e S(π) = 4π.
In general, S(θ) = 4θ.
When the area Δ is demarked, it can be noted that
the sum S(A) + S(B) + S(C) covers the entire
surface of the sphere, and also covers the area Δ
six times. Thus, S(A) + S(B) + S(C) = 4π + 4Δ.
Thus,
4A + 4B + 4C = 4π + 4Δ
or
Δ=A+B+C–π
So the sum of the angles in
a spherical triangle must
exceed 180 = π, otherwise
it would have no area Δ.
The basic formulae of spherical trigonometry can
be derived in several ways. The most concise is
that of Birney in Observational Astronomy, who
considers spherical triangles from the perspective
of how they are connected to the centre of the
sphere. Consider the triangle ABC below, with
sides a, b, and c opposite the angles A, B, and C.
The triangle FDG below is drawn such that FD is
perpendicular to OA, while FG is perpendicular
to the plane AOB. From trigonometry it follows
that:
So:
Also:
So:
Thus:
The same type of analysis can be applied to
derive relationships involving the angle C and
side c. The general formula that applies is
written:
sin A sin a  sin B sin b  sin C sin c
which is the sine formula of spherical
trigonometry.
Memory Aid:
sine angle/sine opposite side = sine angle/sine opposite side
The fundamental formula of spherical
trigonometry is derived in different fashion.
In the spherical triangle ABC the centre of the
sphere is again located at O. Points D, F, and H
are the vertices of a triangle oriented in such a
way that the sides DF and DH are perpendicular
to OA. Note the difference from the previous
diagram. As drawn, the angle FDH is equal to the
angle A. Recall the cosine law from trigonometry,
namely:
a 2  b 2  c 2  2bc cos A
Application of the law to the triangles OHF and
DHF gives:
2
2
2
HF  OH  OF  2OH OF cos a
HF 2  DH 2  DF 2  2DH DF cos A
Subtracting one from the other gives:
0  OH 2  OF 2  2OH OF cos a  DH 2  DF 2  2DH DF cos A
From the Pythagorean Theorem:
2
2
2
OF  DF  OD
OH 2  DH 2  OD 2
So:
0  OD  OD  2OH OF cos a  2 DH DF cos A
2
2
 2 OD  2OH OF cos a  2 DH DF cos A
2
The equation can be solved for cos a by
rearrangement and substitution, namely:
cos a  OD OD  OH OF   DF DH  OH OF  cos A
 OD OF OD OH   DF OF DH OH  cos A
 cos b cos c  sin b sin c cos A
The resulting formula, referred to as the
fundamental formula of spherical trigonometry, is
written:
cos a  cos b cos c  sin b sin c cos A
Memory Aid:
cosine side = cosine adjacent side×cosine adjacent side +
sine adjacent side×sine adjacent side×cosine enclosed angle
There are two other formulae that can be
derived, although their derivation can be found in
Smart’s Spherical Astronomy. It is much less
involved to simply state them:
sin a cos B  cos b sin c  sin b cos c cos A Smart' s Formula C
cos a cos C  sin a cot b  sin c cot B Four Parts Formula
One can usually solve most problems in spherical
astronomy using only the sine and cosine
formulae.
The usefulness of such formulae becomes evident
when one considers how they are applied to
astronomical co-ordinate systems.
Astronomical Co-ordinate Systems:
All co-ordinate systems constructed on spheres
are defined by a fundamental great circle (FGC)
and a reference point (RP) on the FGC.
All co-ordinates are angles measured:
(i) between great circles perpendicular to the
FGC, or
(ii) between small circles parallel to the FGC.
The FGC has two poles, and the RP is defined in
a variety of ways, which accounts for slight
differences from one system to another.
Terrestrial Co-ordinates.
FGC = Earth’s equator, with poles the North Pole
and South Pole.
RP = crossing point of equator by the Greenwich
meridian.
Co-ordinates:
Longitude = angle measured east and west from
the Greenwich meridian. Longitude meridians
are great circles.
Latitude = measured north and south (not plus or
minus) from the Equator. Latitude parallels are
small circles.
Examples: Halifax. 63º 36'.0 W, 44º 36'.0 N
Vancouver. 123º 04'.2 W, 49º 09'.0 N
Problem in terrestrial co-ordinates.
What is the great circle distance between Halifax
and Vancouver, given Earth’s mean radius of
6371 km?
Solution: Sketch the situation with known terms.
12304'.2
90– 4909'.0
6336'.0
90 4436'.0
The corresponding spherical triangle can be
solved for the angular distance d using the cosine
law:
cos a  cos b cos c  sin b sin c cos A
or, here :

 


 
 
cos d  cos 4051' cos 45 24'  sin 4051' sin 45 24' cos 59 28' .2

 0.75642450.702153  0.65408090.7120260.5079894
 0.5311257  0.2365821
 0.7677078
d  cos 1 0.7677078  39.851501
The great circle distance is R d(radians)
= 6371 km (39.851501 × π/180)
= 6371 km × 0.6955399
= 4431 km
Horizon System.
FGC = horizon, with poles the zenith and nadir.
RP = north point.
Co-ordinates:
azimuth = angle measured
through east from 0º to 360.
Azimuth circles are great
circles.
altitude = measured from
horizon towards zenith (positive)
or nadir (negative) from +90º to
–90º. Alternate: zenith distance,
z = 90º – altitude.
Meridian = NS line running through zenith.
Prime vertical = EW line running through zenith.
Use. Airport runways are designated by azimuth
 10°, i.e. runway 33 aligns along azimuth 330°.
Air mass, for correction of photometry, is
calculated from z.
h = height
of plain
parallel
atmosphere
= 1.0
X = h/cos z = h sec z
= sec z (1  0.0012 tan2z) (better)
Photometry from ground level always needs to be
corrected for extinction within the Earth’s
atmosphere, which increases with decreasing
wavelength, i.e. k ~ 1/λ4.
m  m0 = k sec z = kX
where k = extinction coefficient
Earth’s atmosphere also refracts light with a
wavelength dependence, again in proportion to z.
 = actual zenith distance.
z = observed zenith distance.
Then:
sin  = 1.00029 sin z
Denote:
R =   z, the angle of refraction.
Typically, R ≈ 60".29 tan z (undefined at z = 90°)
The refraction at the horizon is denoted as
horizontal refraction, and amounts to R ≈ 33'.
i.e. For z = 90°,  = 90° 33'.
Equatorial System.
FGC = celestial equator (CE, projection on the
sky of Earth’s equator), with poles the north and
south celestial poles, NCP and SCP.
RP = intersection point of meridian with CE
(observer-oriented), or vernal equinox γ (skyorinted).
Co-ordinates:
declination = angle measured
north or south of CE from 0º
to +90 and 90° (δ).
hour angle = angle measured
west of meridian (HA), or
right ascension = angle measured
eastward from vernal equinox (RA).
HA and RA are measured in temporal units and
are equivalent to angles. On the celestial equator:
1h = 15°, 1m = 15', and 1s = 15″, with the equalities
changing by cos δ with increasing declination.
Because of their link to timekeeping, HA and RA
are tied directly to sidereal (star) time and
apparent solar time.
Sidereal time (SidT)= HA(γ)
Apparent solar time = HA() + 12h
Now, HA(γ) = HA(*) + RA(*) = HA() + RA()
Thus, SidT = HA() + RA()
= Apparent solar time  12h + RA()
RA() and δ() during the year are defined by
the apparent motion of the Sun in the sky along
the ecliptic = Sun’s apparent path, and can be
calculated directly or from tables.
Useful values:
Vernal Equinox, March 20:
RA() = 0h, δ() = 0°
Summer Solstice, June 21:
RA() = 6h, δ() = +23½°
Autumnal Equinox, September 23:
RA() = 12h, δ() = 0°
Winter Solstice, December 22:
RA() = 18h, δ() = 23½°
The actual dates of the equinoxes and solstices
slowly change with time. They were March 25,
June 25, September 25, and December 25 when
Julius Caesar modified the original Roman
calendar system (Julian Calendar) in 46 BC.
annual insolation
For many problems it is useful to link the horizon
and celestial systems using the polar triangle.
Interrelationships between the systems are useful
for identifying objects in the sky with points on
the celestial sphere or for determining when
specific objects will be at certain points in the sky.
Note that the cosine law relates the parameters
through:
cos z* = cos(90°φ) cos(90°δ*) +
sin(90°φ) sin(90°δ*) cos HA* , or
cos z* = sin φ sin δ* + cos φ cos δ* cos HA*
where φ is the observer’s latitude on Earth.
Some examples.
1. Suppose φ = 30°N and Betelgeuse crossed the
meridian 2½ hours ago. How far is it from the
zenith?
Solution:
Input data:
φ = +30°
δ(Betelgeuse) = +7° 24' = 7°.4
HA* = 2½h = 2h 30m = 37°.5
 cos z* = sin30° sin7°.4 + cos30° cos7°.4 cos37°.5
= (0.50.1287956) + (0.86602540.99167110.7933533)
= 0.0643978 + 0.6813416 = 0.7457394
 z* = cos1(0.7457394) = 41°.8
So Betelgeuse lies almost 42° from the zenith
when it is 2½ hours past the meridian at a
terrestrial latitude of +30°.
Thought question: How would the answer change
if the observer was located at 30°S rather than N?
2. For how many hours can an observer at 30°N
observe Betelgeuse when its z ≤ 60°? (Since
sec 60° = 2, the situation corresponds to X ≤ 2.)
Solution:
The problem is to obtain Betelgeuse’s HA for z =
60° and double it to get the requested quantity.
Inverting the standard equation gives:
cos HA* = (cos z*  sin φ sin δ*) / cos φ cos δ*
= (cos 60°  sin 30° sin 7°.4) / cos 30° cos 7°.4
= (0.5  0.50.1287956) / (0.86602540.9916711)
= 0.4356022/0.8588123 = 0.5072146
 HA* = cos1(0.5072146) = 59°.521524  15°/h
= 3h.9681016 = 3h 58m
Betelgeuse has X ≤ 2 for 2  3h 58m = 7h 56m.
3. Observations from Arecibo’s radio telescope
(18°N) can only be made for objects with z ≤ 20°.
If an observer wishes to observe a galaxy with δ
= +28°, for how long can it be tracked?
Solution:
Input data:
φ = +18°, and from the last question,
cos HA* = (cos z*  sin φ sin δ*) / cos φ cos δ*
= (cos 20°  sin 18° sin 28°) / cos 18° cos 28°
= (0.9396926  0.30901690.4694715) /
(0.95105650.8829475)
= 0.7946179/0.8397329 = 0.9462746
 HA* = cos1(0.9462746) = 18°.866497  15°/h
= 1h.2577665 = 1h 15m
The galaxy can be observed for 21h 15m = 2h 30m.
4. When is the best time of year to observe the
stars of Orion, RA = 5½h?
Solution:
The optimum time for observing any object is
when it lies on the observer’s meridian at local
midnight, which corresponds to 0h local apparent
solar time (LAST).
i.e. LAST = HA() + 12h = 0h (midnight)
So HA() = 0h  12h = 24h  12h = 12h
Orion is then on the meridian, so local sidereal
time = HA* = 5½h = HA() + RA()
 RA() = 5½hHA() = 5½h12h = 29½h12h = 17½h
The Sun is at RA = 17½h approximately one week
prior to the winter solstice, i.e. around Dec. 15.
Ecliptic System.
FGC = ecliptic, with poles the north and south
ecliptic poles, NEP and SEP.
RP = vernal equinox γ.
Co-ordinates:
celestial (or ecliptic)
longitude, λ = angle
measured eastward
from γ from 0º to 360.
celestial (or ecliptic)
latitude, β = angle
measured from ecliptic.
The system is useful for studies of solar system
objects.
Galactic System.
FGC = Galactic equator (GE), defined by the
Milky Way, with poles the north and south
Galactic poles, NGP and SGP.
RP = direction to the Galactic centre (GC),
defined by Sgr A*.
Co-ordinates:
Galactic longitude, l =
angle measured
Eastward from GC
from 0º to 360.
Galactic latitude, b =
angle measured north or
south of GE from 0º to
+90 and 90°.
Timekeeping.
Apparent solar time is defined by the passage of
the Sun across the sky, but civil time is more
closely related to the motion of the mean Sun, a
fictitious object, across the sky.
Mean solar time = HA(mean Sun) + 12h
The mean Sun differs from the true Sun in the
following way. The true Sun travels along the
ecliptic at a rate that varies according to the
distance of Earth from the Sun. The mean Sun
travels along the celestial equator at a uniform
rate.
Additional complications arise from the use of
time zones and daylight saving time.
The year length varies according to the calendar
system, which has changed from lunar calendars,
through luni-solar calendars, to solar calendars,
such as the Julian Calendar, Gregorian Calendar,
and current modified Gregorian Calendar.
Variable star studies normally cite observations
according to the Julian Date, JD, measured as the
number of sequential days from noon, UT, on
January 1, 4713 BC (named by Joseph Scaliger
after his father Julius Scaliger), or, better yet,
HJD = Heliocentric Julian Date (corrected to the
barycentre of the solar system). Another term,
modified Julian Date, MJD = JD  2400000.5, is
occasionally used.
Precession of the Equinoxes.
The Earth’s axis of rotation precesses about the
perpendicular to the ecliptic as a consequence of
the gravitational influences of the Sun and the
Moon, but not in the fashion
implied by the Wikipedia
figure at right. The sense of
precession is actually
opposite the sense of the
Earth’s rotation.
A top’s
precession.
The effects of precession on the location of the
north celestial pole (NCP) in the sky. Note that
the NCP was located near the bright star Thuban
circa 2700 BC, when
the pyramids were
constructed (see
textbook), and was at
one time located near
Vega, a name that
means “fallen,”
possibly because it has
fallen from its location
near the NCP over
the years.
Precession affects the location of the vernal
equinox γ on the celestial sphere, since the
celestial equator moves as a result of the gradual
realignment of the axis defined by the NCP and
SCP. The location of γ regresses along the
ecliptic, resulting in a constant increase in a star’s
RA, and comparable effects in DEC. The changes
can be expressed as:
Δα = M + N sin α tan δ
Δδ = N cos α
where
M = 1°.2812323T + 0°.0003879T2 + 0°.0000101T3
N = 0°.5567530T  0°.0001185T2  0°.0000116T3
and T = (t  2000.0)/100, with t the current date in
year fractions. See example in textbook.
Archaeoastronomy.
Many constellations bear names originating from
eras when the stellar configuration bore some
resemblance to the object after which they are
named, e.g. Ursa Major, the Great Bear.
Some were named for other reasons, e.g. Hydra.
Stars on the celestial equator (CE) rise due east
and set due west. In 2600 BC Hydra lay along the
CE, making then useful for navigation at night.
Only 50 of the 88
modern constellations
were known in antiquity.
They also outlined only
regions in the northern
sky, most being named
by ancient Minoans.
Ancient star maps.
Zodiacal Constellations, Astrological Eras, and
the link to precession.
The Taurus and Aries Eras.
The Beginnings? The Gemini Era.
The present.
The old constellation of Argo, the Ship, was very
large. It was but one of many symbols associated
with the story of Noah’s Ark.
The Summer
Triangle
Groups that
look like their
namesakes.
Hercules
Normally
pictured
holding the
world.
Sagittarius
An archer?
Better pictured
as a teapot.
The Perseus
Group
A story in the
stars.
Ursa Major
Does this group
truly look like a
bear??!
Stars are presently designated in a variety of
ways: Greek letters, from east to west for stars of
comparable brightness (UMa)…
Greek letters, from from brightest to faintest for
stars of comparable brightness (Ori, Cas), as
well as Bayer-Flamsteed numbers…
and catalogue numbers.
Something different: the General Catalogue of
Variable Stars. All such catalogues are available
on-line these days.
http://cdsarc.u-strasbg.fr/cats/Cats.htx