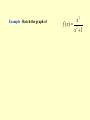* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download + f
Survey
Document related concepts
Transcript
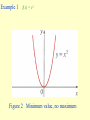
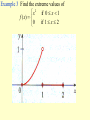
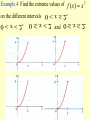
Chapter 3 The mean value theorem and curve sketching 3.3 MONOTONIC FUNCTIONS AND THE FIRST DERIVATIVE TEST In sketching the graph of a function it is very useful to know where it rises and where it falls. The graph shown in Figure1 rises from A to B, falls from B to C, and rises again from C to D. Figure 1 (1) DEFINITION A function f is called increasing on an interval I if f ( x1 ) f ( x2 ) whenever x1 x2 in I . A function that is increasing or decreasing on I is called monotonic on I. TEST FOR MONOTONIC FUNCTIONS Suppose f is continuous on [a, b] and differentiable on (a,b). (a) If f'(x) > 0 for all x in (a,b), then f is increasing on [a, b]. (b) If f'(x) < 0 for all x in (a, b), then f is decreasing on [a, b]. PROOF (a) Let x1 and x2 be any two numbers in [a, b] with x1<x2 . Then f is continuous on [x1, x2] and differentiable on (x1, x2), so by the Mean Value Theorem there is a number c between x1 and x2 such that (2) Now f '(c) > 0 by assumption and x2 -x1> 0 because x1<x2 . Thus the right side of Equation 2 is positive, and so f ( x2 ) f ( x1 ) f (c)( x2 x1 ) This shows that f is increasing on [a,b]. It is similar to prove (b). f ( x2 ) f ( x1 ) 0 or f ( x1 ) f ( x2 ). Example 1 Find where the function f (x) = 3x4 - 4x3 - 12x2 +5 is increasing and where it is decreasing. THE FIRST DERIVATIVE TEST Suppose that c is a critical number of a continuous function f. (a) If f ' changes from positive to negative at c, then f has a local maximum at c. (b) If f ' changes from negative to positive at c then f has a local minimum at c. (c) If f ' does not change sign at c (that is f ' is positive on both sides of c or negative on both sides), then f has no local extremum at c. Example 3 Find the local and absolute extreme values of the function f(x)= x3(x -2)2, -1 3. Sketch its graph. x f(6/5)=1.20592 is a local maximum; f(2)=0 is a local minimum; absolute maximum value is f(3)=27; absolute minimum value is f(-1)=-9. The sketched in Figure 6. 3.4 CONCAVITY AND POINTS OF INFLECTION Figure 1 Figure 2 (a) Concave upward (b) Concave downward (1) DEFINITION If the graph of f lies above all of its tangents on an interval I, then it is called concave upward on I. If the graph of f lies below all of its tangents on f , it is called concave downward on I. Figure 3 shows the graph of a function that is concave upward (abbreviated CU) on the intervals (b, c), (d, e), and (e,p) and concave downward (CD) on the intervals (a, b), (c,d), and (p,q) THE TEST FOR CONCAVITY Suppose f is twice differentiable on an interval I. (a) If f "(x) > 0 for all x in I, then the graph of f is concave upward on I. (b) If f"(x) < 0 for all x in I, then the graph of f is concave downward on I. The equation of this tangent is y f (a) f (a)( x a) we must show that f ( x) f (a) f (a)( x a) whenever x I ( x a) (See Figure 4.) Figure 4 Proof of (a) First let us take the case where x > a. Applying the Mean Value Theorem to f on the interval [a,.x], we get a number c, with a < c < x, such that (2) f (x) - f(a) == f’ (c) (x - a) Since f " > 0 on f we know from the Test for Monotonic Functions that f ' is increasing on I. Thus, since a < c, we have f'(a)<f’(c) and so, multiplying this inequality by the positive number x -a ,we get (3) Now we add f(a) to both sides of this equality: f(a) +. f'(a) (x - a) < f(a) + f'(c) (x - a) But from Equation 2 we have f(x) = f(a) + f'(c) (x -a). So this inequality becomes (4) f(x)>f(a) +f '(a)(x-a) f (a)( x a) .f (c)( x a) which is what we wanted to prove. For the case where x < a,we have f'(c) < f'(a), but multiplication by the negative number x - a reverses the inequality, so we get (3) and (4) as before. (2) DEFINITION A point P on a curve is called a point of inflection if the curve changes from concave upward to concave downward or from concave downward to concave upward at P. Example 1 Determine where the curve y=x3 -3x+1 is concave upward and where it is concave downward. Find the inflection points and sketch the curve. THE SECOND DERIVATIVE TEST Suppose f " is continuous on an open interval that contains c. (a) If f '(c)=0 and f "(c) > 0, then f has a local minimum at c. (b) If f '(c)=0 and f "(c) < 0, then f has a local maximum at c. Example 2 Discuss the curve y = x4 - 4x3 with respect to concavity, points of inflection, and local extrema. Use this information to sketch the curve. Since f '(3) = 0 and f "(3) >0,f (3) = -27 is a local minimum. The point (0,0) is an inflection point since the curve changes from concave upward to concave downward there. Also (2, -16) since the curve changes from concave downward to concave upward there. 3.5 Limits at infinity, horizontal asymptotes Figure 1 (1) DEFINITION Let f be a function defined on some interval , Then lim f ( x) L means that the values of f (x) can be made arbitrarily close to L by taking x sufficiently large. x (2) DEFINITION Let f be a function defined on some interval ( , a), Then lim f ( x) L x means that the values of f(x) can be made arbitrarily close to L by taking x sufficiently large negative. (3) DEFINITION The line y = L is called a horizontal asymptote of the curve y = f(x) if either lim f (x) = L or lim f (x) = L x x (4) THEOREM If r >0 is a rational number, then 1 lim that is0defined for all x, then If r > 0 is a rational number such r x x 1 lim r 0 x x Infinite limits at infinity The notation lim f ( x) x is used to indicate that the values of f(x) become large as x becomes large.Similar meanings are attached to the following symbols: lim f ( x) x lim f ( x) lim f ( x) x x Example 1 Example 2 (5) DEFINITION Let f be a function defined on some interval . Then ( a, ) means that for every N such that therefis( axcorresponding number lim )L x whenever x > N. 0 f ( x) L (6) DEFINITION Let f be a function defined on some interval . Then (, a ) means that for every such that lim f ( x) L there is a corresponding number N x whenever x < N. 0 f ( x) L (7) DEFINITION (a, )Let f be a function defined on some interval . Then lim f ( x ) means that for every positive M there is a corresponding number N such that x whenever x > N. f ( x) M 3.6 Curve sketching (1) This section is to discuss how to sketch the graph of a curve. In high school we learnt to plot points and join the points in order. Example 2 y=x (2) In this section we will draw the graph by following steps: A. Domain The first step is to determine the domai of the function f. B. Intercept Find the x- and y-intersepts . C. Symmetry (i) even (ii) odd (iii) periodic D. Asymptotes: (i) Horizontal asymptotes (ii)Vertical asymptotes (iii)slant asymptotes E. Intervals of increase or decrease Use the test for monotonic functions. F. Local maximum and minimum valuves Find the critical numbers of f. G. Concavity and points of inflection Compute f"(x) and use the test for concavity. H. Sketch the curve Using the information in A---G , draw the graph. Example Discuss the curve 2 2x y 2 x 1 Solution A.Domain B. Intercept C. Symmetry D. Asymptotes E. Intervals of increase or decrease F. Local maximum and minimum values G. Concavity and points of inflection H. Sketch the curve Slant asymptotes Some curves have asymptotes that are oblique, that is, neither horizontal nor vertical. lim [ f ( x) (mx b)] 0 x If , then the line y=mx+b is called a slant asymptotes, because the vertical distance between the curve y=f(x) and the line y=mx+b approaches 0. 3 Example Sketch the graph of x f ( x) 2 x 1 3.9 Applications to Economics Cost function C (x ) Average function If the average cost is a minimum, then marginal cost = average cost Example 1 A company estimates that the cost (in dollars) of producing x items is (a) Find the cost, average cost, and marginal cost of producing 1000 items, 2000 items, and 3000 items. (b) At what production level will the average cost be lowest, and what is this minimum average cost? Solution (a) The average cost function is C ( x) 2600 c ( x ) 2 0 . 001 x The marginal cost function x is x C'(x) = 2 + 0.002x (b) To minimize the average cost we must have marginal cost = average cost C'(x) = c(x) 2 + 0.002x = 2600/x+ 2 + 0.001x This equation simplifies to 0.001x = 2600/x so x2 =2600/0.001 = 2,600,000 and To see that this production level actually gives a minimum we note that c"(x) =5200/x3> 0, so c is concave upward on its entire domain. The minimum average cost is x 2,600,000 1612 c(1612) = 2600/1612+2+0.001(1612) = $5.22/item Let p(x) be the price per unit that the company can charge if it sells x units. Then p is called the demand function (or price function) and we would expect it to be a decreasing function of x. If x units are sold and the price per unit is p(x), then the total revenue is R(x) = x p(x) and R is called the revenue function (or sales function). The derivative R' of the revenue function is called the marginal revenue function and is the rate of change of revenue with respect to the number of units sold. If x units are sold, then the total profit is P(x) = R(x) - C(x) and P is called the profit function. The marginal profit function is P', the derivative of the profit function. In order to maximize profit we look for the critical numbers of P, that is, the numbers where the marginal profit is 0. But if P'(x) = R'(x) - C'(x) = 0 then R'(x) = C'(x) Therefore If the profit is a maximum, then marginal revenue = marginal cost To ensure that this condition gives a maximum we could use the Second Derivative Test. Note that P"(x) = R"(x) - C"(x) < 0 when R"(x) < C"(x) and this condition says that the rate of increase of marginal revenue is less than the rate of increase of marginal cost. Thus the profit will be a maximum when R'(x) = C'(x) and R"(x) < C"(x) Example 2 Determine the production level that will maximize the profit for a company with cost and demand functions C(x) = 3800 + 5x - x2/1000 p(x) = 50 - x/100 SOLUTION The revenue function is R(x) = x p(x) = 50x -x2/100 so the marginal revenue function is R'(x) = 50 -x/50 and the marginal cost function is C'(x)=5-x/500 Thus marginal revenue is equal to marginal cost when 50-x/50=5-x/500 Solving, we get x = 2500 To check that this gives a maximum we compute the second derivatives: R"(x) = -1/50 C"(x) = -1/500 Thus R"(x) < C"(x) for all values of x. Therefore a production level of 2500 units will maximize profits. 3.10 Antiderivatives We know how to solve the derivative problem: given a function, find its derivative. But many problems in mathematics and its applications require us to solve the inverse of the derivative problem: given a function, find a function F whose derivative is f. If such a function F exists, it is called an antiderivative of f. (1) DEFINITION A function F is called an antiderivative of f on an interval I if F '(x) = f (x) for all x in I. (2) THEOREM If F is an antiderivative of f on an interval I, then the most general antiderivative of f on I is F(x) + C where C is an arbitrary constant. (3) Table of antidifferntiation formulas Some of the most important applications of differential calculus are optimization problems, in which we are required to find the optimal (best) way of doing something. In many cases these problems can be reduced to finding the maximum or minimum values of a function. Let us first explain exactly what we mean by maximum and minimum values. 3.1 MAXIMUM AND MINIMUM VALUES Figure 1 Minimum value f(a) Maximum value f(d) In Figure 1, if we consider only values of x near b [for instance, if we restrict our attention to the interval (a,c)], then f(b) is the largest of those values of f(x) and is called a local maximum value of f. Likewise, f(c) is called a local minimum value of f because f(c) f(x) for x near c [in the interval (b, d), for instance]. The function f also has a local minimum at e. In general we have the following definition. Example 1 f(x) = x2 Figure 2 Minimum value, no maximum Example 2 Please find the absolute maximum, the absolute minimum, local maximum and local minimum of the function f ( x) 3x 16 x 18x 4 3 2 1 x 4 We have seen that some functions have extreme values, while others do not. The following theorem gives conditions under which a function is guaranteed to possess extreme values. (3) THE EXTREME VALUE THEOREM If f is continuous on a closed interval [a,b], then f attains an absolute maximum value f(c) and an absolute minimum value f(d) at some numbers c and d in [a, b]. The extreme value theorem is illustrated in the following. Figure 5 Example 3 Find the extreme values of 2 x if 0 x 1 f ( x) if 1 x 2 0 Example 4 Find the extreme values of f ( x) x 2 0 x 2 , on the different intervals 0 x 2, 0 x 2 and 0 x 2. (4) FERMAT' S THEOREM If f has a local extremum (that is, maximum or minimum) at c, and if f '(c) exists, then f '(c) =0. (5) DEFINITION A critical number of a function f is a number c in the domain of f such that either f '(c) = 0 or f '(c) does not exist. (6) If f has a local extremum at c, then c is a critical number of f . (7) To find the absolute maximum and minimum values of a continuous function f on a closed interval [a, b]: 1. Find the values of f at the critical numbers of f in (a, b). 2. Find the values of f(a) and f(b). 3. The largest of the values from steps 1 and 2 is the absolute maximum value; the smallest of these values is the absolute minimum value. Example 5 Find the absolute maximum and minimum values of the function 1 3 2 f ( x) x 3 x 1 x 4 2 3.2 THE MEAN VALUE THEOREM We will see that many of the results of this chapter depend on one central fact, which is called the Mean Value Theorem. But to arrive at the Mean Value Theorem we first need the following result. ROLLE'S THEOREM Let f be a function that satisfies the following three hypotheses: 1. f is continuous on the closed interval [a, b]. 2. f is differentiable on the open interval (a,b). 3. f(a)=f(b) Then there is a number c in (a,b) such that f '(c) = 0. Figure 1 PROOF There are three cases: CASE I f(x) = k, a constant. Then f '(x) = 0, so the number c can be taken any number in (a,b). CASE II f(x)> f(a) for some x in (a, b) [as in Figure l(b) or (c)] By the Extreme Value Theorem (which we can apply by hypothesis 1) f has a maximum value somewhere in [a, b]. Since f (a) = f (b), it must attain this maximum value at a number c in the open interval (a, b). Then f has a local maximum at c and, by hypothesis 2, f is differentiable at c. Therefore f '(c) = 0 by Fermat's Theorem. CASE lll f(x) < f(a) for some x in (a,b) [as in Figure l (c) or (d)] By the Extreme Value Theorem, f has a minimum value in [a, b] and, since f(a) = f(b), it attains this minimum value at a number c in (a,b). Again f '(c) = 0 by Fermat's Theorem. Example 1 Prove that the equation x3 + x -1 = 0 has exactly one real root. SOLUTION First we use the Intermediate Value Theorem (1,5.9) to show that a root exists. To show that the equation has no other real root we use Rolle's Theorem and argue by contradiction. THE MEAN VALUE THEOREM Let f be a function that satisfies the following hypotheses: 1. f is continuous on the closed interval [a, b]. 2. f is differentiable on the open interval (a, b). Then there is a number c in (a,b) such that (1) f (b) f (a) f (c) ba or, equivalently, (2) f (b) f (a) f (c)(b a) we can see that it is reasonable by interpreting it geometrically. The slope of the secant line AB is f (b) f (a) mab ba PROOF The equation of the line AB can be written as f (b) f (a) f (b) f (a) y f (a) ( x a) or as y f (a) ( x a) ba ba Figure 5 f (b) f (a) (3) h( x) f ( x) f (a) ( x a) ba First we must verify that h satisfies the three hypotheses of Rolle's Theorem 1. The function h is continuous on [a, b] because it is the sum of f and a first-degree polynomial, both are continuous. 2. The function h is differentiable on (a, b) because both f and the first-degree polynomial are differentiable. In fact, we can f (b) f (a) compute h' directly from Equation 4: h ( x) f ( x) ba 3. h(a) =h(b). f (b) f (a) 0 h(c) f (c) ba Since h satisfies the hypotheses of Rolle's Theorem, that theorem says there is a number c in (a, b) such that h’ (c) =0. Therefore and so f (b) f (a ) f (c) ba Example 2 To illustrate the Mean Value Theorem with a specific function, let us consider f (x) = x3 - x , a = 0, b = 2. Figure 6 illustrates this calculation: the tangent line at this value of c is parallel to the secant line OB. Figure 6 The Mean Value Theorem can be used to establish some of the basic facts of differential calculus. One of these basic facts is the following theorem. (3) THEOREM If f ' (x) = 0 for all x in an interval (a, b), then f is constant on (a, b) (4) COROLLARY If f '(x) = g'(x) for all x in an interval (a, b), then f - g is constant on (a,b); that is , f (x) = g(x) + c where c is a constant.