* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Document
Photon polarization wikipedia , lookup
Quantum tunnelling wikipedia , lookup
Quantum state wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Quantum gravity wikipedia , lookup
Casimir effect wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Higgs boson wikipedia , lookup
Large Hadron Collider wikipedia , lookup
Quantum field theory wikipedia , lookup
Double-slit experiment wikipedia , lookup
Old quantum theory wikipedia , lookup
Weakly-interacting massive particles wikipedia , lookup
Atomic nucleus wikipedia , lookup
Nuclear structure wikipedia , lookup
Supersymmetry wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
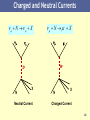
ALICE experiment wikipedia , lookup
Identical particles wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Theory of everything wikipedia , lookup
Renormalization group wikipedia , lookup
Search for the Higgs boson wikipedia , lookup
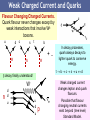
Canonical quantization wikipedia , lookup
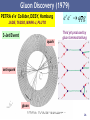
Quantum electrodynamics wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Scalar field theory wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
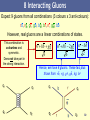
Higgs mechanism wikipedia , lookup
History of quantum field theory wikipedia , lookup
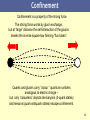
Minimal Supersymmetric Standard Model wikipedia , lookup
Technicolor (physics) wikipedia , lookup
Renormalization wikipedia , lookup
Electron scattering wikipedia , lookup
ATLAS experiment wikipedia , lookup
Future Circular Collider wikipedia , lookup
Strangeness production wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
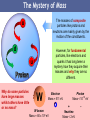
Grand Unified Theory wikipedia , lookup
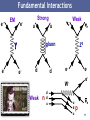
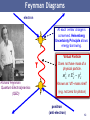
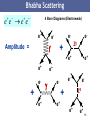
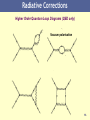
Particle Physics 2 Prof. Glenn Patrick Quantum, Atomic and Nuclear Physics, Year 2 University of Portsmouth, 2012 - 2013 1 Last Week - Recap Particle Physics & Cosmology Matter Particles, Generations Spin – Fermions & Bosons Charged Leptons Antimatter Neutral Leptons - Neutrinos Hadrons Strange Particles and Strangeness Symmetries, Conservation Laws Quantum Numbers, Isospin Eightfold Way and Quark Model Charm, Bottom, Top, Quark Counting 2 Today’s Plan BOOKS 20 November Particle Physics 2 B.R. Martin & G. Shaw, Force Carriers Particle Physics, 3rd Edition, Four Fundamental Interactions Wiley Quantum Field Theory Donald H. Perkins, Introduction to High Energy Feynman Diagrams Physics, 4th edition, CUP Higher Orders/Radiative Corrections Coughlan et al, The Ideas of Anomalous magnetic moment of muon Particle Physics, Cambridge Charged and Neutral Currents Z and W Vector Bosons Gluons Colour Charge and Quantum Chromodynamics (QCD) Unification of Fundamental Forces, Running Coupling Constants Higgs Boson and Field Copies of Lectures: http://hepwww.rl.ac.uk/gpatrick/portsmouth/courses.htm 3 I II III Observed in 2000 4 Force Carriers Last week we looked at the Matter Particles (quarks and leptons). This week we look at the four gauge bosons that make up the Force Particles. Now the smallest Particles of Matter may cohere by strongest Attractions, and compose bigger Particles of weaker Virtue. There are therefore Agents in Nature able to make Particles of Bodies stick together by very strong Attractions. And it is the business of experimental Philosophy to find them out. ISAAC NEWTON (1680) 5 The Four Forces of Nature STRONG WEAK ELECTRO MAGNETIC GRAVITY 6 Forces in Classical Physics Classically, forces are described by charges and fields Field is a physical quantity which has a value for each point in space-time. 7 Can be a scalar or vector field. Quantum Field Theory Quantum Mechanics + Relativity Forces are transmitted by exchange of force particles between matter particles. 4 forces with different force particles. Heisenberg Uncertainty Principle Energy ΔE is “borrowed for a time Δt Maximum distance of exchange particle Et t E x ct Mc 1 Range of Force mass of exchange particle Photon has zero mass, so infinite range If we associate M with the pion mass, we get the Yukawa potential that we saw 8 when we talked about the “nuclear force” in Nuclear Physics 1. Four Forces of Nature STRONG FORCE ELECTROMAGNETIC FORCE Strength: 1, Range: 10-15 m Exchange: Gluon Strength: 1/137, Range: Infinite Exchange: Photon A FIFTH FORCE? GRAVITY WEAK FORCE Strength: 6x10-39 m, Range: Infinite, Exchange: ? Strength: 10-6 m, Range: 10-18 m Exchange: W±, Z0 Modified gravity? Dark matter, Dark energy, etc. 9 g S2 S ~1 4c EM e2 1 ~ 4c 137 GF m 2p ~ 10 5 10 GN m 2p ~ 10 36 Fundamental Interactions e- EM e- Strong u u e- e Weak gluon e- d d Z0 e- ee- WWeak n d d u e u d u e p 11 Feynman Diagrams electron At each ‘vertex’ charge is conserved. Heisenberg Uncertainty Principle allows energy borrowing. Virtual Particle Does not have mass of a physical particle. m X2 E X2 p X2 Richard Feynman Quantum Electrodynamics (QED) Known as “off –mass shell” (e.g. not zero for photon) positron (anti-electron) 12 Feynman Diagrams Annihilation Exchange External legs represent amplitudes of initial and final state particles. Positron is drawn as electron travelling backwards in time. Internal lines (propagators) represent amplitude of exchanged particle. Charge, baryon number and lepton number conserved at each vertex. Quark flavour conserved for strong and EM interactions. Vertices represent coupling strength of interacting particles. Perturbation theory. Expand and keep the most important terms for calculations. 13 Feynman Diagrams Associate each vertex with the square root of the appropriate coupling constant, i.e. √𝛼. When the amplitude is squared to yield a cross-section there will be a factor 𝛼 𝑛 , where n is the number of vertices (known as the “order” of the diagram). For QED: Lowest order Second order e2 1 4c 137 Add the amplitudes from all possible diagrams to get the total amplitude, M, for a process transition probability. 2 2 Transition Rate M (phase space) Fermi’s Golden Rule 14 Bhabha Scattering e e e e 4 Born Diagrams (Electroweak) e- Amplitude = e- e- eZ0 + e+ e+ e- + e+ e+ e+ e- e- eZ0 + e+ e+ e+ 15 Radiative Corrections Higher Order Quantum Loop Diagrams (QED only) Vacuum polarisation 16 Anomalous Magnetic Moment of the Muon Dirac theory predicts g=2, but this is modified by quantum fluctuations. e+ e- QED e+ e+ e- B Z0 WEAK µ µ µ µ W µ W e- 3rd order corrections e+ e- + STRONG Radiation and re-absorption of virtual photons contributes an anomalous magnetic moment. 1 a ( g 2) 0.00116 Lowest order correction 2 2 a (exp) 116592089 10 11 (0.54 ppm) a (the) 116591802 10 11 (0.42 ppm) a 287 80 10 11 ~3.6σ effect New Physics? 17 Hundreds of diagrams! Muon g-2: Testing the Standard Model athe aQED ahad aweak anew Experimental measurements of aμ Beyond the Standard Model (BSM) Physics? Uncertainty on aμ and physics reach as the uncertainty has decreased. J.P. Miller et al, Ann. Rev. Nucl. Part. Sci., 62 (Nov. 2012), 237 18 Photon – EM Boson 1900 Planck Black Body Radiation explained in terms of light quanta Nobel Prize. Quantum energy of photon E h h = Planck’s constant = frequency 1905 Einstein explained the Photoelectric Effect in terms of quanta of energy Nobel Prize. 1925 G.N. Lewis proposed the name Photon for quanta of light. 1925 Compton showed quantum (particle) nature of X-rays Nobel Prize. 19 Charged and Neutral Currents N X N X W+ Z0 N - X Neutral Current N X Charged Current 20 Discovery of Weak Neutral Currents (1973) Bremsstrahlung effects electron e e 21 21 Gargamelle Bubble Chamber Z and W Story Carlo Rubbia (UA1) Two Experiments: UA1 and UA2. Rubbia came up with idea and led UA1. 1984 Simon van der Meer Super Proton Synchrotron turned into proton-antiproton collider. Stochastic cooling technique. UA1 UA2 22 W Boson Discovery – UA1 (1982) 𝒑 + 𝒑 → 𝑾± + 𝑿 𝑾± → 𝒆± + 𝝂(𝝂) “Missing Energy” = neutrino Type equation here. electron 23 Z Boson Discovery – UA1 (1983) 𝒑 + 𝒑 → 𝒁𝟎 + 𝑿 𝒁𝟎 → 𝒆+ + 𝒆− electron positron 24 Weak Charged Current and Quarks Flavour Changing Charged Currents. Quark flavour never changes except by weak interactions that involve W± bosons. u d c s t b + .. W W W tbcsud decay finally understood! W- n d d u In decay processes, quark always decays to lighter quark to conserve energy. u d u e p Weak charged current changes lepton and quark flavours. Possible that flavour changing neutral currents exist beyond (tree level) Standard Model. 25 Gluon Discovery (1979) PETRA e+e- Collider, DESY, Hamburg JADE, TASSO, MARK-J, PLUTO e e qq g Third jet produced by gluon bremsstrahlung 3-Jet Event quark anti-quark gluon 26 Inside the Proton There are 3 “valence” quarks inside the proton bound together by gluons. Quantum theory allows quarks to change into quark-antiquark pairs for a short time. There is a bubbling “sea” of gluons, quarks and antiquarks. There is however a problem with the basic quark model….. 27 Colour Charge Some particles apparently contain quarks in the same state violates Pauli Exclusion Principle (e.g. ++ = uuu). Proposed that quarks carry an extra quantum number called “colour”. Red Green Blue Quarks Cyan Magenta Yellow Anti-quarks All physical particles are colour neutral or “white”. baryon meson 28 Quark Species quarks antiquarks u u d d c c u d c s s t t b b s t b u up down d charm c strange s top t bottom b u u d c d c s s t t b b 29 8 Interacting Gluons Expect 9 gluons from all combinations (3 colours x 3 anti-colours): rb, rg, gr, gb, bg, br, rr, gg, bb However, real gluons are a linear combinations of states. This combination is colourless and symmetric. Does not take part in the strong interaction. rr bb gg 3 rr bb 2 gg 6 rr bb 2 Hence, we have 8 gluons. These two plus those from 𝑟𝑏, 𝑟𝑔, 𝑔𝑟, 𝑔𝑏, 𝑏𝑔, 𝑏𝑟 30 Counting Colours In Particle Physics 1, we counted quarks. Can also count colours using R. below top energy threshold 31 Quantum Chromodynamics (QCD) Quantum Chromodynamics (QCD) is the theory of the Strong Interaction in the Standard Model. Gluons carry colour+anti-colour charge, e.g. red-anti blue. Colour charge always conserved so quarks can change colour when emitting a gluon. Since gluons (8) carry colour charge, they can interact with one another! Fragmentation If a quark is pulled from a neighbour, the colour field “stretches”. At some point, it is easier for the field to snap into two new quarks. 32 Confinement Confinement Confinement is a property of the strong force. The strong force works by gluon exchange, but at “large” distance the self-interaction of the gluons breaks the inverse square-law forming “flux tubes”: Quarks and gluons carry “colour “ quantum numbers analogous to electric charge – but only “colourless” objects like baryons (3-quark states) and mesons (quark-antiquark states) escape confinement. 33 Quark Interactions Only one pair of quarks interact, the rest are spectators. 34 Residual Forces How do molecules form if atoms are electrically neutral? Residual EM Force Electrons in one atom are attracted to protons in another atom. How do protons bind to form the nucleus? Protons & neutrons are colour neutral. Residual Strong Interaction between quarks in different protons overcomes EM repulsion. 35 Force Particles Bosons = Spin 1 Force Particle Charge Mass (GeV) 0 Strong gluon (g) 0 EM photon () 0 0 Weak Z0 boson W boson 0 1 91.2 80.4 Relative Strength 1 Range (m) 10-15 1/137 infinite 10-5 10-18 Bosons = Spin 2 Gravity graviton 0 (not observed yet!) 0 10-39 infinite 36 36 Particles and Forces Summary of how different particles feel the different forces: u quark d quark electron e c quark s quark muon t quark b quark tau Charge +2/3 -1/3 -1 0 +2/3 -1/3 -1 0 +2/3 -1/3 -1 0 Strong Yes Yes No No Yes Yes No No Yes Yes No No EM Yes Yes Yes No Yes Yes Yes No Yes Yes Yes No Weak Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes 37 Unification of the Forces Grand Unification – Unite strong interaction with electroweak interaction. Grand Unified Theories (GUTs) predict that protons are unstable. ~Planck scale Final step would then be to add quantum gravity to form a Theory of Everything (TOE). Because gravitons interact with one another field theory is nonre-normalisable. Graviton has not been discovered! Planck Units Length Time Energy Temp 1.62 x 10-35 m 5.39 x 10-44 s 19 2 1.22 x 10 3832 GeV/c 38 1.42 x 10 K Electroweak Force or EW symmetry breaking 39 Running Coupling Constants e2 at low energy 1 4 0 c 137.035999074 GF M 2 c 5 ~ 1 . 03 10 Weak W 3 g S2 ( E ) ~1 Strong S ( E ) c GN M 2 40 ~ 5 10 Gravity g 4c EM coupling constant 𝛼 = fine structure constant Coupling constants have an energy dependence due to (higher order) virtual interactions. These change the measured value of the coupling constant and make it depend on the energy scale at which it is measured (logarithmic dependence). The strong and weak couplings decrease with energy whilst the EM coupling increases. It is therefore possible that at some energy scale, all 3 forces 40 become equal. Grand Unification Grand-Unified Theories (GUT), favoured, (e.g. by non-zero 𝜈 masses) predict the 3 coupling constants (QED, Weak, QCD) to unify at GUT scale of 3x1016 GeV. This unification does not happen in the Standard Model (+GUT), but does in Supersymmetry with a 1 TeV scale. Starting from the measured values of αQED(mZ) and sin2W as input, one can predict: S (mZ ) 0.073 0.002 (Standard GUT) S (mZ ) 0.129 0.010 (SUSY GUT) Standard Model + GUT LEP, Amaldi et al, 1991 To be compared to the experimental value (mostly constrained by LEP): S (mZ ) 0.118 0.003 Baryon Number violated in GUTs. Conflict with measurements? ( p e 0 ) 1034 yrs (SuperK) SUSY at 1 TeV + GUT 41 Missing Ingredient: Higgs Sector Generates mass? Graviton not yet found 42 The Mystery of Mass The masses of composite particles like protons and neutrons are mainly given by the motion of the constituents. u d However, for fundamental particles, like electrons and quarks it has long been a mystery how they acquire their masses and why they are so different. u Why do some particles have large masses whilst others have little or no mass? W Electron Mass = 511 eV W boson Mass = 80 x 109 eV Photon Mass < 10-18 eV e Neutrino Mass < 2 eV 43 Top Quark Heavier than Silver Atom! M(top) = 172 GeV ± 0.9 ± 1.3 GeV Silver (A=108) 44 Higgs Mechanism Standard Model in basic form leads to massless particles. 1961- 1968: Glashow, Weinberg & Salam developed theory that unifies EM and weak forces into one electroweak force. Predicted weak neutral current. Nobel Prize: 1979 1964: Higgs, Kibble, Brout, Englert et al introduced the Higg’s field. Gives mass to Z and W bosons. Nobel Prize: ?? Peter Higgs 1971: Veltman, t Hooft - Solved the problems of infinities through renormalisation. Nobel Prize: 1999 Higgs boson is a neutral, scalar (spin=0) particle. Coupling to particles is proportional to their mass. No prediction for Higgs mass. Vacuum should be filled with Higgs field – boson is the quantum of this field 45 in the same way that the photon is the quantum of the EM field. Space is not Empty The classical vacuum just consists of empty space-time and is featureless. In reality, it’s sea of virtual particle-antiparticle pairs from quantum fluctuations. Vacuum is the state of minimum energy for the Universe. WARNING: Quantum field theory gives cosmological constant (or zero point energy) 120 orders of magnitude too high! 46 Higgs Field and Higgs Boson Higg’s Boson H H H H H H H H H H H H H Higg’s Field 47 Mexican Hat Potential State in which the Higgs field is zero is not the lowest energy state. EM - Electric & Magnetic Fields (Vector) Energy lowest when field is zero. EW - Higgs Field (Scalar) Energy lowest when field is not zero. Law is basically symmetric, but equilibrium state is not. Symmetry is said to be spontaneously broken. 48 Electroweak Symmetry Breaking At high enough temperatures, particles were (symmetrically) massless. As the Universe cooled, ring of stable points appeared. W and Z got mass from the field, but the stayed massless. 49 Higgs Hunting Indirect Fit to LEP EW Measurements Direct Searches at LEP Collider f e- f Z* Z0 H e+ f f mH 114.4 GeV (95% CL) Also, limits from Tevatron Preferred Value 29 94 - 24 GeV mH 185 GeV (95% CL)50 Higgs Particle Discovery? 4 Jul 2012, CERN 51 Francois Englert & Peter Higgs 𝑯 → 𝜸𝜸 𝑪𝒉𝒂𝒏𝒏𝒆𝒍 Higgs does not couple to zero mass photon. Possible via a top quark loop. CMS ATLAS Phys. Lett. B 716 (17 Sept 2012), Issue 1 52 𝑯 → 𝒁𝒁∗ → 𝟒ℓ 𝑪𝒉𝒂𝒏𝒏𝒆𝒍 ℓ 𝒎𝒆𝒂𝒏𝒔 𝒍𝒆𝒑𝒕𝒐𝒏 ATLAS Phys. Lett. B 716 (17 Sept 2012), Issue 1 CMS 53 Higgs Particle – Properties? MASS M H 126.0 0.4( stat ) 0.4( sys) GeV ATLAS M H 125.3 0.4( stat ) 0.5( sys) GeV CMS Phys. Lett. B 716 (17 Sept 2012), Issue 1 Spin/Parity of Standard Model Higgs is expected to be JP = 0+ Spin 0 consistent with decay channels seen so far. Spin 1 already ruled out. The first scalar elementary particle. 54 Higgs Spin Spin is quantised and measured wrt an axis. Sz = -S, -S+1, -S+2, … +S-1, +S However, photon is massless, so in this case Sz can only be +1 or -1 c/o Aidan Randle, ATLAS ATLAS and CMS will need to do a proper spin analysis by analysing angular 55 distributions of decay products to get the definitive answer. Beyond the Standard Model? ● 18 input parameters from experiment (e.g. particle masses, coupling constants). ● Gravity not included. Hierarchy problem. ● Why 3 generations of particles? ● Are these particles fundamental? ● What is mass? (Higg’s particle) ● Missing antimatter? ● Missing matter (dark matter & dark energy)? ● Neutrino masses. ● Cosmological constant predicted 56 to be 10120 too large for vacuum. End CONTACT Professor Glenn Patrick email: [email protected]