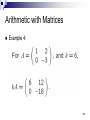Download Matrix Review

390 Codes, Ciphers,
and Cryptography
Polygraphic Substitution
Ciphers – Matrix Review
Polygraphic Substitution Cipher




A polygraphic substitution cipher is one in which
blocks of plaintext characters are replaced by blocks of
ciphertext characters.
The Playfair cipher and Double Playfair cipher (see
Singh’s Appendix E and NOVA’s Decoding Nazi Secrets
webpage) are examples of polygraphic substitution
ciphers!
Another famous polygraphic cipher is Hill’s System,
which was invented by American mathematician Lester
Hill in 1931.
To understand Hill’s scheme, we need to review some
matrix theory!
2
Matrix Definition

A matrix is a rectangular
array of elements (usually
numbers) written in rows
and columns.

Example 1: Some
matrices:
3
Matrix Definition

Example 1 (cont.):






Matrix A is a 3 x 2 matrix of
integers.
A has 3 rows and 2
columns.
Matrix B is a 2 x 2 matrix of
rational numbers.
Matrix C is a 1 x 4 matrix of
elements of Z26.
We also call C a row vector.
A matrix consisting of a single
column is often called a
column vector.
4
Matrix Definition

Notation:
5
Arithmetic with Matrices
Matrices of the same size (i.e. same
number of rows and same number of
columns), with elements from the same
set, can be added or subtracted!
 The way to do this is to add or subtract
corresponding entries!

6
Arithmetic with Matrices
7
Arithmetic with Matrices

Example 2: For matrices A and B given
below, find A+B and A-B.
8
Arithmetic with Matrices

Example 2 (cont):
Solution:

Note that A+B and A-B are the same size as A
and B, namely 2 x 3.
9
Arithmetic with Matrices

Matrices can also be multiplied. For AB to make sense, the
number of columns in A must equal the number of rows in B.
10
Arithmetic with Matrices

Example 3: For matrices A and B given below,
find AB and BA.
11
Arithmetic with Matrices



Example 3 (cont.):
A x B is a 3 x 2 matrix. To get the row i, column j entry of this matrix, multiply
corresponding entries of row i of A with column j of B and add.
Since B has 2 columns and A has 3 rows, we cannot find the product BA (#
columns of 1st matrix must equal # rows of 2cd matrix).
12
Arithmetic with Matrices
Another useful operation with matrices is
scalar multiplication, i.e. multiplying a
matrix by a number.
 For scalar k and matrix A, kA=Ak is the
matrix formed by multiplying every entry of
A by k.

13
Arithmetic with Matrices

Example 4:
14
Identities and Inverses





Recall that for any real number a,
a+0 = 0+a = a and (a)(1) = (1)(a) = a.
We call 0 the additive identity and 1 the multiplicative identity
for the set of real numbers.
For any real number a, there exists a real number -a, such that
a+(-a) = -a+a = 0.
Also, for any non-zero real number a, there exists a real number
a-1 = 1/a, such that
(a-1)(a) = (a)(a-1) = 1.
We all -a and a-1 the additive inverse and multiplicative
inverse of a, respectively.
15
Identities and Inverses

For matrices, we also have an additive identity and
multiplicative identity!
16
Identities and Inverses
A+0 = 0+A = A and AI = IA = A holds.
(HW-check!)
17
Identities and Inverses

Clearly, A+(-A) = -A + A = 0 follows! Note also that B-A = B+(-A)
holds for any m x n matrices A and B.
18
Identities and Inverses

Example 5:
19
Identities and Inverses

Example 5 (cont):
20
Identities and Inverses

Example 5 (cont.)
21
Identities and Inverses

Example 5 (cont.)
22
Identities and Inverses

Example 5 (cont):
23
Identities and Inverses
For multiplicative inverses, more work is
needed.
 For example, here is one way to find the
matrix A-1, given matrix A, in the 2 x 2
case!

24
Identities and Inverses
25
Identities and Inverses





From the first matrix equation, we see that e, f, g, and h must satisfy the
system of equations:
ae + bg = 1
af + bh = 0
ce + dg = 0
cf + dh = 1.
One can also show that if e, f, g, and h satisfy this system, then the second
matrix equation above also holds!
Solving the system of equations, we find that ad-bc  0 must hold and
e = d/(ad-bc),
f = -b/(ad-bc),
g = -c/(ad-bc),
h = a/(ad-bc).
Thus, we have the following result for 2 x 2 matrices:
26
Identities and Inverses



In this case, we say A is invertible.
If ad-bc = 0, A-1 does not exist and we say A is
not invertible.
We call the quantity ad-bc the determinant of
matrix A.
27
Identities and Inverses

Example 6: For matrices A and B below,
find A-1 and B-1, if possible.
28
Identities and Inverses




Example 6 (cont.)
Solution: For matrix A, ad-bc = (1)(4)-(2)(3)= 4-6 = -20, so A
is invertible. For matrix B, ad-bc = (3)(2)-(1)(6) = 6-6 = 0, so
B is not invertible.
HW-Check that AA-1 = A-1A = I!!
Note: For any n x n matrix, A-1 exists, provided the
determinant of A is non-zero.
29
Linear Systems of Equations
One use of matrices is to solve systems of
linear equations.
 Example 7: Solve the system
x + 2y = 1
3x + 4y = -1
 Solution: This system can be written in
matrix form AX=b with:

30
Linear Systems of Equations

Example 7 (cont.)

Since we know from Example 6 that A-1 exists,
we can multiply both sides of AX = b by A-1 on
the left to get:
A-1AX = A-1(AX)= A-1b => X = A-1b.
Thus, we get in this case:

31
Linear Systems of Equations

Example 7 (cont.):
32
References
Elementary Linear Algebra (4th ed) by
Howard Anton.
 Cryptological Mathematics by Robert
Edward Lewand (section on matrices).

33