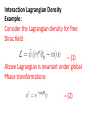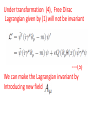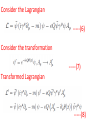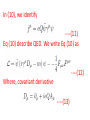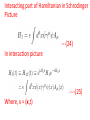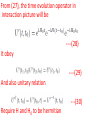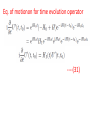Download Document

Chapter V
Interacting Fields
Lecture 1
Books Recommended:
Lectures on Quantum Field Theory by Ashok
Das
 Advanced Quantum Mechanics by Schwabl
Interaction Lagrangian Density
Example:
Consider the Lagrangian density for free
Dirac field
---(1)
Above Lagrangian is invariant under global
Phase transformations
---(2)
Invariance of (1) under (2) lead to conserved
current
----(3)
Now, consider the invariance of Eq (1) under
Transformations in which phase angle
Function of space-time coordinates i.e.
--(4)
Under transformation (4), Free Dirac
Lagrangian given by (1) will not be invariant
----(5)
We can make the Lagrangian invariant by
Introducing new field
Consider the Lagrangian
-----(6)
Consider the transformation
-----(7)
Transformed Lagrangian
-----(8)
Comparing (6) and (8)
----(9)
Recall that the above transformation leave
the free Lagrangian of e.m. field invariant.
We identify
as photon field and in (6)
Introduce corresponding free term
-----(10)
In (10), we identify
----(11)
Eq (10) describe QED. We write Eq (10) as
----(12)
Where, covariant derivative
----(13)
Example 2: Phi-four theory
λ dimensionless coupling constant.
Self-interactions of Higgs field in electroweak
theory involve above interaction.
Eq of motion:
Example 3: Yukawa Theory
g is dimensionless coupling constant.
Use: Interaction of nucleons with pions
In standard model, scalar Higgs field couple
Quarks and leptons.
Remark: Any QFT should be renormalizble.
In perturbation theory higher order terms will
Involve integrals over 4-momenta of virtual
Particles.
To avoid divergence cut off parameter Λ is used
At end one again takes
and if physical
quantity remain independent of Λ, we say
theory is renormalizable.
Suppose theory have coupling constants having
dimensions mass raise to power negative
dimensions.
Coupling constant is multiplied by factor having
dimension mass raise to power positive
dimensions so that scattering amplitude is
dimensionless. This quatitiy will be and
When we take
theory will
Not remain renormalizble.
Theory should not have coupling constant with
–Ve mass dimensions.
•Action is dimensionless
• Lagrangian density should have dimension
mass4 or simple 4 .
Scalar filed d = 1, Fermion , d = 3/2
E.M field, d = 1 .
Now consider in scalar theory
d =1,
d=0
For n>4 i.e.
.
No terms will be allowed as coupling constant
then should have dimension 4-n, which is –ve
and theory will diverge.
• Spinor self interactions are not allowed
e.g.
, d = 9/2. Not Lorentz invariant.
•
allowed.
•Vector-spinor interaction QED
• Scalar QED Lagrangian
• Vector self interactions
Interaction Representation
The Lagrangian or Hamiltonian for an
interacting system can be divided into
Free part and interacting part
----(14)
If interaction Lagrangian do not have derivative
Term, then the corresponding interacting part
of Hamiltonian will be
----(15)
In Schrodinger picture
-----(16)
In interaction picture
--(17)
Eq. of motion
---(18)
Notations in interaction picture in subsequent
Discussion
-----(19)
Eq. Of motion for field operators
---(20)
Since interacting part of Lagrangian does not
contain derivative terms and therefore, the
canonical conjugate fields remain same
-----(21)
Equal time commutation relations of
Interacting fields are same as for free fields.
The interacting fields obey the same
commutation relations as the free fields.
The plane waves (spinor solutions, free
photons, and free mesons) are still
solutions of the equations of motion and
lead to the same expansion of the field
operators as in the free case.
The Feynman propagators are still same.
Schrodinger and Heisenberg operators are
related through
----(22)
In interaction representation
---(23)
Interacting part of Hamiltonian in Schrodinger
Picture
---(24)
In interaction picture
----(25)
Where, x = (x,t)
Time evolution operator in interaction picture
In Schrodinger picture:
---(26)
In interaction picture:
---(27)
From (27), the time evolution operator in
interaction picture will be
----(28)
It obey
----(29)
And also unitary relation
---(30)
Require H and H0 to be hermitian
Eq. of motionon for time evolution operator
----(31)