* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Ideal Transformer Model
Induction motor wikipedia , lookup
Electrical ballast wikipedia , lookup
Ground (electricity) wikipedia , lookup
Power engineering wikipedia , lookup
Electric machine wikipedia , lookup
Power inverter wikipedia , lookup
Current source wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Stepper motor wikipedia , lookup
Voltage regulator wikipedia , lookup
Stray voltage wikipedia , lookup
Single-wire earth return wikipedia , lookup
Electrical substation wikipedia , lookup
Voltage optimisation wikipedia , lookup
Buck converter wikipedia , lookup
Rectiverter wikipedia , lookup
Three-phase electric power wikipedia , lookup
Opto-isolator wikipedia , lookup
Earthing system wikipedia , lookup
History of electric power transmission wikipedia , lookup
Mains electricity wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Resonant inductive coupling wikipedia , lookup
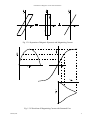
Introduction to Magnetic Circuits and Transformers Transformer Modeling and Analysis 1.1 The Ideal Transformer One of the most important magnetic circuit devices is the transformer which makes possible changing the level of voltage (and current) in any ac system with very little power loss, voltage drop or waveform distortion. Properly designed transformers are so nearly "ideal" that in many applications a model which neglects the inevitable imperfections but correctly represents the fundamental performance properties is adequate. This idealized model is referred to as an ideal transformer. The basic structure of a two winding, shell type transformer is shown in Fig. 1.1.1 It consists of a magnetic core with two windings arranged so that to as great an extent as possible they link the same magnetic flux. In the figure the main (or mutual) flux which links both windings is illustrated by the heavy black arrows. Note that in this shell type core the main flux divides in two and returns in the outside legs of the core. The designations primary and secondary are arbitrary except that it is common to think of the winding connected to the power source as the primary winding. Main (or Mutual) Flux . . . . . . . . . . . . . . . . Primary Winding Secondary Winding . . . . + + + + + + + + + + + + + + + + Core Fig. 1.1.1 Shell Type Transformer. To develop a model of an ideal transformer, the following assumptions are necessary: 1) the resistances of the coils are negligible. 2) the flux is entirely confined to the core and thus totally links both windings. March, 2007 1 Introduction to Magnetic Circuits and Transformers 3) the core requires no MMF to support flux (infinite permeability) and has negligible core loss. Assumptions 1 and 2 applied with Faraday's Law lead immediately to the first of the equations describing the ideal transformer, since with zero resistance dφ1 v1 = N1 dt dφ2 v2 = N2 dt (1.1.1) Since the flux is the same for each winding, φ1 = φ2 and therefore v2 v1 = N1 N2 . (1.1.2) This result demonstrates the voltage level changing ability of a transformer. Note that the voltage waveform is faithfully reproduced for any ac waveform for which the assumptions are valid (these limitations are described later). Note also that this result is not limited to only two windings, it can be generalized to any number of windings v2 v3 v1 = = N1 N2 N3 vn =.........= N . n (1.1.3) and is perhaps best remembered as "the volts per turn is a constant in a transformer". The second equation describing the ideal transformer results from Ampere's Law and the assumption that a negligible MMF is required in the core to support the flux. Writing Ampere's Law around the core encircling the windings as shown in Fig 1.1.2 yields N1i1 – N2i2 = Hiron liron = 0 (1.1.4) This equation indicates that the currents are transformed in the inverse way as the voltages; a necessary result since the input and output power of the transformer must be equal because there are no active elements inside the device. As with the voltage equation, this result can be generalized to any number of windings N1i1 ± N2i2 ± N3i3 ± ....... ±Nnin = 0 (1.1.5) where the signs of the terms depend on the way the currents are assigned relative to the coil directions. When the current references are chosen to all produce flux in the same direction all the signs are positive and the relation is best remembered as "the sum of all the MMF's is zero". March, 2007 2 Introduction to Magnetic Circuits and Transformers . . . . . . . . . . . . . . . . . . . . + + + + + + + + + + + + + + + + Ampere's Law Path Fig. 1.1.2 Ampere's Law Path for Determination of Current Law The matter of coil polarity is usually handled in theoretical work by placing "dot marks" on the terminals that have the same relative polarity. For voltage this means the marked terminals go positive at the same time. For currents it means currents into the marked terminals all produce MMF in the same direction. In real transformers coil terminals are often sequentially numbered and all even numbered terminals have the same relative polarity. For a two winding transformer the voltage and current relations in Eqs. 1.1.2 and 1.1.4 can be used to derive an impedance transformation relationship as follows. For a secondary side impedance defined by – –Z = V2 2 – I2 (1.1.6) the input impedance can be written as N1 – – V2 –Z = V1 = N2 1 – N2 – I1 N1 I 2 N1 = N 2 –Z 2 2 (1.1.7) which demonstrates that impedances are transformed by the square of the turns ratio when viewed on the opposite side of a transformer. This property is often used in situations where "impedance matching" is desired and is also very useful in analytically manipulating circuits containing transformers to reduce circuit complexity for calculations. March, 2007 3 Introduction to Magnetic Circuits and Transformers 1.1.1 Example - Ideal Transformer Model To illustrate the application of the ideal transformer model and especially determination of the correct signs in the equations, consider the three winding transformer shown in Fig. 1.1.3. In using the model the first step is to select the reference directions for all of the currents and voltages. This selection is totally arbitrary but is often made to minimize the number of minus signs which will occur in the resulting equations. The choices in Fig. 1.1.3 have been made to create minus signs for purposes of illustration. . + v N 2 2 i2 . . – – v1 N1 i1 N3 + + i3 v3 – Fig. 1.1.3 Three Winding Transformer with References Selected For the voltage references in the figure, Eq 1.1.3 becomes v1 –N 1 v2 =N 2 v3 =N 3 (1.1.8) where the minus sign on the v1 / N1 term occurs because the reference on v 1 is opposite to that on v2 and v3. The ampere turn equation for the current references in the figure is N1i1 – N2i2 + N3i3 = 0 (1.1.9) since the direction of i2 is opposite to that of i1 and i3. 1.2 Ideal Autotransformers Although transformers are often used to conductively decouple circuits as well as to change voltage levels, a considerable reduction in size is possible if a conductive connection between primary and secondary is permissible. The size reduction is made possible by the fact that an interconnection between primary and secondary allows addition or subtraction of the primary and secondary voltages and currents thus increasing the rating over that of the two winding, conductively decoupled connection. March, 2007 4 Introduction to Magnetic Circuits and Transformers As an example, consider the autotransformer connection shown in Fig. 1.2.1. From the diagram in the figure, the volt-amperes delivered at the input is N1 N1 VAin = v1(i1 + i2) = v1(i1 + N i1) = v1i1 (1+ N ) 2 (1.2.1) 2 while that at the output is N1 N1 VAout = i2(v1 + v2) = i2(N v2+ v2) = v2i2 (1+ N ) 2 . + v N 2 i1+ i2 2 + i2 v1 + v . – + Source (1.2.2) 2 v1 N1 2 Load i1 – – Fig 1.2.1 Two Winding Transformer Used As An Autotransformer As is required the input and output volt-amperes are equal since v 1i1 = v2i2 and the allowable rating of the autotransformer compared to the two winding transformer is VAA VAT = N1 v1i1 (1+ N ) 2 v1i1 N1 = 1+ N 2 (1.2.3) The amount of increase in rating depends on the turn ratio N1 /N 2 of the original two winding transformer with a large ratio giving a large increase. The voltage ratio of the autotransformer is v1 + v 2 = v1 N2 v1 + N v1 1 v1 N2 = 1+ N 1 (1.2.4) so that a large rating increase corresponds to a small ratio of output to input voltage in the autotransformer. Thus, whenever a small change in voltage level is needed, an autotransformer connection should be considered since it results in a much smaller size magnetic device. It is often argued that the increase in rating occurs because a portion of the transferred power is conductively transferred and in fact this is the case since the VA which are actually magnetically transferred at full March, 2007 5 Introduction to Magnetic Circuits and Transformers power are exactly equal to the two winding transformer rating. Probably the most commonly used autotransformer is the "Variac" used in most laboratories as a variable voltage ac supply. 1.3 Transformer Resistances and Reactances While it is possible to design transformers which function very nearly as ideal transformers in specific applications, there are always parasitic effects which become apparent at the extremes of the operating envelope or are allowed to become significant for size, cost or other design related reasons. These parasitic effects are primarily associated with the three assumptions stated earlier and repeated here for convenience. Ideal transformer assumptions: 1) the resistances of the coils are negligible. 2) the flux is entirely confined to the core and thus totally links both windings. 3) the core requires no MMF to support flux (infinite permeability) and has negligible core loss. The principal transformer parasitics will now be described and incorporated into a more complete transformer equivalent circuit model. Winding Resistance While the resistances of the windings can be kept small by using appropriate size wire for a specific application, the resistance can never be made zero. Typically the IR drop at full current is kept less than 1 or 2% of rated voltage and often less than this in large transformers (scaling relations indicate that the resistance and pu resistance inherently decrease as a transformer is made larger). To incorporate the winding resistances into a transformer model it is only necessary to connect appropriate resistors in series with the primary and secondary windings of the ideal transformer as shown in Fig.1.3.1. R2 R1 Ideal + + + + i 2 i1 v e e v . . 1 – 1 2 – – N1 N 2 – 2 Fig. 1.3.1 Transformer Equivalent Circuit Showing Winding Resistances March, 2007 6 Introduction to Magnetic Circuits and Transformers Winding Leakage Inductance The second assumption which states that all of the flux links every winding is also never totally true because of the spatially distributed nature of the magnetic flux. Conceptually, one can divide the flux into main or mutual flux and leakage flux as illustrated in Fig. 1.3.2 in which the space between the windings where the leakage flux exists has been exaggerated. The ideal transformer relations then apply to the mutual flux part of the total flux and the leakage flux is treated as a parasitic. The voltage associated with the leakage flux subtracts from the input voltage in the same way as the IR drop and reduces the voltage applied to the ideal transformer. The relations are φ1 = φl + φm (1.3.1) where φl is the leakage flux and φm is the mutual flux as shown in the center post of Fig 1.3.2. The total voltage produced by φ1 is dφl dφ1 dφm v1 = N1 dt = N1 dt + N1 dt = e1l + e1 (1.3.2) Main (or Mutual) Flux . . . . . . . . . . . . . . . . . . . . + + + + + + + + + + + + + + + + Leakage Flux Fig. 1.3.2 Concept of Main (or Mutual) Flux and Leakage Flux March, 2007 7 Introduction to Magnetic Circuits and Transformers where e 1l is the voltage produced by the leakage flux in the primary winding. The voltage e1 is produced by the mutual flux in the primary winding and is the voltage applied to the ideal transformer portion of the model in Fig. 1.3.1. By definition the leakage flux is that flux that links one winding but not the second winding. Although often represented as having components associated with each winding individually, the magnetic structure of a transformer is such that it can only realistically be defined by reference to both windings simultaneously, The leakage flux passes through the air space occupied by the windings and is produced by the combination of the MMF's N1i1 and N2i2 as illustrated in Fig 1.3.3. As suggested by the dashed Amperes Law paths in the figure, the MMF driving the leakage flux is provided by the winding currents, starting with zero MMF at the center post iron, building up in an approximately linear fashion to N1i1 at the interwinding space and then dropping back to zero across the secondary winding as a result of the ampere turn balance N1i1 = N2i2. It is apparent from the figure that the leakage flux passing between the two windings links the winding closest to the center post (considered to be the primary for this discussion) but does not link the outer winding. Main (or Mutual) Flux Leakage Flux . . . . . . . . N1I1 . . . . . . . . . . . . + + + + + + + + + + + + + + + + Sample Ampere’s Law Paths for Evaluation of MMF Creating Leakage Flux MMF Distribution Creating Leakage Flux Fig. 1.3.3 Leakage Flux Paths and MMF Distribution Creating the Leakage Flux March, 2007 8 Introduction to Magnetic Circuits and Transformers Because a large portion of the leakage path length is in air and because the MMF driving the leakage is N1 i1 , the primary leakage flux is for practical purposes a linear function of the primary current i1, which allows writing the leakage voltage flux as φ1l = P l N1i1 (1.3.3) where Pl is the permeance of the leakage path. The leakage voltage e1l can then be expressed as dφ1l dN1P li1 di1 di1 = (N1)2P l dt = L1l dt e1l = N1 dt = N1 dt (1.3.4) where L 1l is the leakage inductance referred to the primary. A similar development can be carried out for the secondary leading to the leakage inductance referred to the secondary. The only difference in the two is the turns L1l = (N1)2P l L2l = (N2)2P l (1.3.4) which can also be interpreted as referring the leakage reactance through the ideal transformer in the circuit model. R2 R1 L 1l Ideal + + + + i 2 i1 v e e v . . 1 – 1 2 – – N1 N 2 – 2 Leakage Referred to Primary L 2l R1 + + v1 – R2 Ideal i1 . . + e e1 – + i2 2 – N1 N v 2 – 2 Leakage Referred to Secondary Fig. 1.3.4 Transformer Equivalent Circuit Showing Resistances and Leakage Reactances March, 2007 9 Introduction to Magnetic Circuits and Transformers The parasitic resistance and leakage flux of a real transformer are thus represented by series resistances and inductances connected in series with an ideal transformer. The voltages which appear across these series elements subtract from the input voltage and thus alter the actual voltage ratio of the transformer in comparison to the ideal value equal to the turns ratio. In a well designed transformer the departure from the ideal is small under normal conditions. In cases of operation at the extremes of possible operation, for example at short circuit on the secondary, the parasitic resistance and leakage inductance are the whole story and they determine the amount of short circuit current. It is often convenient to shift all the resistance and leakage inductance to one side of the transformer using the impedance relation in Eq. 1.1.7. If this is done by transferring the secondary values to the primary, the result is N1 Req1 = R1 + N 2 R2 (1.3.5) Leq1 = L1l (1.3.6) 2 Fig.1.3.5 illustrates the resulting simplified circuit. Req L eq1 1 + + v1 Ideal i1 – . . e e1 – i2 2 – N1 N + + v 2 – 2 Fig. 1.3.5 Simplified Equivalent Circuit with all Resistance and Leakage Inductance Referred to Primary Magnetizing Inductance and Core Loss The remaining principal parasitic is the influence of the large but finite permeability of the core and the losses caused by the ac core flux. The finite permeability modifies Eq.1.14, repeated here for convenience, March, 2007 10 Introduction to Magnetic Circuits and Transformers N1i1 – N2i2 = Hiron liron = 0 (1.1.4) in that Hiron is no longer zero. As a result the sum of the ampere turns is no longer exactly zero; the ampere turns of the winding supplied by the source must be a bit larger than the second winding to supply the required magnetizing MMF. This is conveniently modeled by defining an exciting current i1ex which supplies the required core MMF and losses according to the relation N1i1ex = Hiron liron + loss component (1.3.7) i1 = i1id + i1ex (1.3.8) with With these definitions, Eq. 1.1.4 without the (= 0) becomes N1 (i1id + i1ex ) – N2i2 = Hiron liron + loss component and using Eq 1.3.7 results in N1i1id – N2i2 = 0 (1.3.9) The concept is illustrated in Fig.1.3.6. The primary current is viewed as having two components; i1ex which supplies the necessary MMF and power to create the core flux and i1id which provides the useful interaction with the secondary winding following the ideal transformer laws. i1 i 1id + + v1 – i 1ex i2 Ideal . . e1 – + + e v 2 – N1 N 2 – 2 Fig. 1.3.6 Equivalent Circuit Showing Exciting Current Resulting from Finite Core Permeability and Core Losses The remaining task is to determine the nature of i1ex and means of representing it in terms of a simple circuit model. Two limiting cases are of value in understanding the nature of the exciting current. First, consider the case of finite, constant core permeability and zero core loss. In this case the core is easily modeled as having a constant permeance and the core flux is then given by March, 2007 11 Introduction to Magnetic Circuits and Transformers µcAc φm = l N1i1ex =P cN1i1ex c (1.3.10) which leads to the magnetizing inductance L m N1 φm Lm = i = ( N1) 2 P c 1ex (1.3.11) Second, consider the case where the core is infinitely permeable (so L m is infinite) but there are eddy current losses in the core. The eddy currents are created by the voltage produced in the core by the time changing core flux - exactly the same process that creates the voltages in the transformer windings. A resistive load on a winding will therefore absorb power in a very similar fashion as the eddy current losses. It is therefore reasonable to model the eddy current loss as a resistor connected such that it is exposed to a voltage generated by the core flux. These two limiting cases lead to the circuit shown in Fig. 1.3.7, which is also the most common form of representation of the excitation and core loss requirements of a real transformer. While strictly speaking the model is only valid for constant permeability and for eddy current losses, it is used as an approximation for the more realistic situations where saturation creates variable permeability and where the core loss includes hysteresis loss. i2 i1 i 1id Ideal + + + + i . . 1ex i 1c – e e1 v1 2 v 2 i 1m – – N1 N – 2 Fig. 1.3.7 Equivalent Circuit Showing Magnetizing and Core Loss Currents To demonstrate that the circuit of Fig. 1.3.7 is a reasonable model for a system with magnetic hysteresis, consider the flux-current characteristics shown in Fig. 1.3.8. As shown in the figure, the total flux-current characteristic for any steady state flux cycle can be separated into a roughly rectangular hysteresis loop and the associated magnetizing current curve. Focusing on the hysteresis loop, note that March, 2007 12 Introduction to Magnetic Circuits and Transformers λ λ i λ i i Fig. 1.3.8 Separation of Magnetic Hysteresis and Magnetizing Current λ λ i t i t Fig. 1.3.9 Waveform of Magnetizing Current with Saturated Core March, 2007 13 Introduction to Magnetic Circuits and Transformers whenever the flux is increasing the current required is positive (in the case shown, a positive constant). Since from Faraday's Law an increasing flux requires a positive voltage, both the voltage and current are positive and thus "in phase" as in a resistor. For a material with a true rectangular hysteresis loop the current is a rectangular wave in time which is in phase with the voltage wave (and independent of the voltage waveform). For realistic designs the magnetizing current curve almost always shows some saturation and this results in a magnetizing current which is non-sinusoidal when the applied voltage is sinusoidal. The relationships are illustrated in Fig. 1.3.7. Here it is assumed that the IR drop is negligible and hence the sinusoidal voltage results in a sinusoidal flux linkage. However the saturation non linearity of the core maps this sinusoidal flux linkage into a magnetizing current which has a peak in the center of the flux wave and thus near the zero crossings of the voltage wave. Note that it is important to keep this nonsinusoidal current small enough so the resulting IR drop is small compared to the input voltage or flux waveform distortion (and hence output voltage distortion) will occur. 1.4 Transformer Equivalent Circuit Combining the concept of leakage flux and inductance depicted in Fig. 1.3.4 and that of main flux and magnetizing inductance depicted in Fig. 1.3.7 yields the generally accepted transformer equivalent circuit shown in Fig. 1.4.1. L 1l = L eq1 R1 + i1 i 1ex i 1id v1 + . . Rm L m + e e1 i 1c – R2 Ideal i 1m – 2 – N1 N + i2 v 2 – 2 Fig 1.4.1 Transformer Equivalent Circuit Because of the quality of most well designed transformers (i.e. small R1 , R2 , L1l and large Rm and Lm) it is seldom necessary to use the full circuit in the form shown in Fig 1.4.1. For example: March, 2007 14 Introduction to Magnetic Circuits and Transformers 1) Rm and L m can usually be neglected except for operation at light load, when efficiency is being evaluated or if greater than rated voltage is applied. Req L 1l = L eq1 1 Ideal + + v1 i1 – . . L 1l e e1 – + + i2 – – N1 N v 2 2 2 Fig 1.4.2 Transformer Equivalent Circuit with Rm and Xm Neglected 2) In large transformers or high frequency transformers the resistances are typically small compared to ωL1l and can be neglected along with Rm and Lm. The equivalent circuit then reduces to a single reactance equal to ωL 1l or ωL 2l depending on which side of the ideal transformer is modeled. L 1l = L eq1 + + v1 – Ideal i1 . . e e1 – + + i2 2 – N1 N v 2 – 2 Fig 1.4.3 Transformer Equivalent Circuit with Req, Rm and Xm Neglected 3) Often the reactance X1l or X2l is small compared to other impedances in the circuit and can be neglected. The transformer equivalent circuit then becomes that of an ideal transformer. Ideal + + + + i2 i1 v e e v . . 1 – 1 2 – – N1 N 2 – 2 Fig 1.4.4 Ideal Transformer - All Parasitics Neglected 1.5 Transformer Core Materials and Core Construction Historically, electric motors, transformers and inductors have been constructed from magnetic steels usually in the form of thin laminations, electrical conductors (either copper or aluminum), March, 2007 15 Introduction to Magnetic Circuits and Transformers insulation for the conductors and slots, high tensile strength steel for shafts and steel or copper alloys for bearings. The laminations used in most general purpose motors, transformers and inductors have been “common iron” or low carbon steel. Although low in cost, this material typically produces devices of only modest efficiency. More recently, high efficiency designs often feature higher quality silicon steels at a correspondingly higher cost. The percent of silicon in the steel has a beneficial effect in reducing losses in the steel but at the same time tends to reduce the saturation flux density. The percent of silicon in motor steels typically ranges from 1% to 3.25%. The corresponding losses range from 0.6 watt per pound of core for the 3.25% steel to 1.0 watt per pound for the 1% silicon steel at a flux density of 15,000 gauss (1.5 tesla). Nickel alloys, such as permalloy, have low losses but are very expensive and have low saturation flux density. The cobalt alloys such as Supermendur (49% iron, 49% cobalt and 2% vanadium) have peak flux densities over 20,000 gauss, but are also very expensive and have higher losses. When the magnetic structure is assembled by means of stacking laminations punched from thin sheet material, the volume occupied by the stacked laminations does not truly represent the volume of iron that supports the magnetic flux. A region whose permeability is that of air exists between the laminations because of the presence of irregularities in the laminations or due to a thin coat of insulating varnish applied to avoid circulating current flow between laminations (eddy currents). In order to allow for this effect, the effective cross- sectional area of iron is equal to the cross-sectional area of the stack times a factor called the stacking factor. This factor, defined as the ratio of the cross sectional area of the actual iron to the cross sectional area of the stack, ranges between about 0.95 and 0.90 for lamination thickness between 0.025 inch and 0.014 inch (25 and 14 mil) respectively. For thinner laminations, for example 1 mil to 5 mil thick, the stacking factor can be in the range of 0.4 to 0.75. Thinner laminations than 14 mil are generally not used at 60 hz unless iron loss is a severe problem but are common at higher frequencies, for example in aircraft generators or higher switching frequency power supplies. A new group of alloys has already been developed grouped under the generic title of amorphous metal alloys. These materials represent a new state of matter for electromagnetic materials, the so called amorphous or non-crystalline state. Ordinary window glass is a typical example of an amorphous material. Some of these new amorphous alloys have magnetic properties which surpass the properties of conventional alloys. Thus, they appear to be a potentially useful new class of soft magnetic material. These alloys contain about 80% ferritic elements such as iron, nickel and cobalt, and 20% glasseous elements such a silicon, phosphorous, boron, and carbon. A good example of an amorphous alloy having 80% iron and 20% boron by atomic weight is Fe80B 20 (Allied Chemical’s Metglass). Major advantages of amorphous metal include low cost, very low core loss ( one fifth that of the best silicon steels), low annealing temperature and high tensile strength. Unfortunately, this new material has not yet been used on a large scale at typical power line frequencies because the high tensile strength also March, 2007 16 Introduction to Magnetic Circuits and Transformers makes the material difficult to punch or otherwise utilize in conventional structures. Also, amorphous materials are presently only available in thicknesses of 1 to 2 mils (0.001” to 0.002”) which results in a poor stacking factor and creates problems during assembly. Tape wound cores for applications up to 10 to 20 khz are available and represent an important alternative at these frequencies. An important class of materials for higher frequency devices (from low audio frequencies to several hundred megahertz) are the soft ferrites. Ferrites are ceramic materials composed of various oxides with iron oxide as the main ingredient. They offer low loss combined with high permeability, very high resistivity (virtually all of the core loss is hysteresis loss) and are easily produced in a wide range of shapes. Disadvantages include limited flux densities, brittleness and low thermal conductivity. A wide variety of material types exist to cover the very large frequency range served by ferrites. Ferrite is very often the only realistic choice in high frequency applications and the core selection process is essentially one of finding the best ferrite type for the specific task. Because of the very high electrical resistivity the losses in ferrites at typical operating frequencies are almost entirely hysteresis losses. As a result the loss is linearly dependent on frequency and virtually independent of the waveform of the flux. These statements follow from the hysteresis energy loss dependence on the area of the hysteresis loop and thus on the number of loops per second for the power loss. Waveform independence follows from the fact that the rate at which portions of the loop are traversed does not matter; only the area of the total loop is significant. There is an exception to the waveform independence for loops containing a minor loop as shown in Fig. 1.5.1. Creation of a minor loop requires that the direction of flux change be reversed and subsequently rereversed. This in turn requires that the polarity of the induced voltage change sign (have multiple zero crossings) as illustrated in Fig. 1.5.1. The hysteresis loss is generally increased by the minor loop since part of the area of the loop is covered twice. Powdered materials provide another important class of core materials, especially for inductors. These cores generally have low but highly controlled relative permeability in the range of ten to a few hundred. Typical materials include molypermalloy, nickel-iron and iron-aluminum-silicon. In general these materials provide the equivalent of a distributed air gap and can provide significant improvement in performance compared to a conventional core plus air gap design. March, 2007 17 Introduction to Magnetic Circuits and Transformers B Minor Loop H Negative Voltage Creating Minor Loop v(t) t Fig.1.5.1 Illustration of Creation of a Minor Loop and Associated Increase of Hysteresis Loss March, 2007 18