Download Ideal Transformer Model

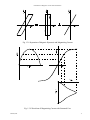
Introduction to Magnetic Circuits and Transformers
Transformer Modeling and Analysis
1.1 The Ideal Transformer
One of the most important magnetic circuit devices is the transformer which makes possible
changing the level of voltage (and current) in any ac system with very little power loss, voltage drop or
waveform distortion. Properly designed transformers are so nearly "ideal" that in many applications a
model which neglects the inevitable imperfections but correctly represents the fundamental performance
properties is adequate. This idealized model is referred to as an ideal transformer.
The basic structure of a two winding, shell type transformer is shown in Fig. 1.1.1 It consists of a
magnetic core with two windings arranged so that to as great an extent as possible they link the same
magnetic flux. In the figure the main (or mutual) flux which links both windings is illustrated by the
heavy black arrows. Note that in this shell type core the main flux divides in two and returns in the
outside legs of the core. The designations primary and secondary are arbitrary except that it is common
to think of the winding connected to the power source as the primary winding.
Main (or Mutual) Flux
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Primary Winding
Secondary Winding
.
.
.
.
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Core
Fig. 1.1.1 Shell Type Transformer.
To develop a model of an ideal transformer, the following assumptions are necessary:
1) the resistances of the coils are negligible.
2) the flux is entirely confined to the core and thus totally links both windings.
March, 2007
1
Introduction to Magnetic Circuits and Transformers
3) the core requires no MMF to support flux (infinite permeability) and has negligible core loss.
Assumptions 1 and 2 applied with Faraday's Law lead immediately to the first of the equations
describing the ideal transformer, since with zero resistance
dφ1
v1 = N1 dt
dφ2
v2 = N2 dt
(1.1.1)
Since the flux is the same for each winding, φ1 = φ2 and therefore
v2
v1
=
N1
N2 .
(1.1.2)
This result demonstrates the voltage level changing ability of a transformer. Note that the voltage
waveform is faithfully reproduced for any ac waveform for which the assumptions are valid (these
limitations are described later). Note also that this result is not limited to only two windings, it can be
generalized to any number of windings
v2
v3
v1
=
=
N1
N2
N3
vn
=.........= N .
n
(1.1.3)
and is perhaps best remembered as "the volts per turn is a constant in a transformer".
The second equation describing the ideal transformer results from Ampere's Law and the assumption
that a negligible MMF is required in the core to support the flux. Writing Ampere's Law around the
core encircling the windings as shown in Fig 1.1.2 yields
N1i1 – N2i2 = Hiron liron = 0
(1.1.4)
This equation indicates that the currents are transformed in the inverse way as the voltages; a necessary
result since the input and output power of the transformer must be equal because there are no active
elements inside the device. As with the voltage equation, this result can be generalized to any number of
windings
N1i1 ± N2i2 ± N3i3 ± ....... ±Nnin = 0
(1.1.5)
where the signs of the terms depend on the way the currents are assigned relative to the coil directions.
When the current references are chosen to all produce flux in the same direction all the signs are positive
and the relation is best remembered as "the sum of all the MMF's is zero".
March, 2007
2
Introduction to Magnetic Circuits and Transformers
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Ampere's Law Path
Fig. 1.1.2 Ampere's Law Path for Determination of Current Law
The matter of coil polarity is usually handled in theoretical work by placing "dot marks" on the
terminals that have the same relative polarity. For voltage this means the marked terminals go positive
at the same time. For currents it means currents into the marked terminals all produce MMF in the same
direction. In real transformers coil terminals are often sequentially numbered and all even numbered
terminals have the same relative polarity.
For a two winding transformer the voltage and current relations in Eqs. 1.1.2 and 1.1.4 can be used
to derive an impedance transformation relationship as follows. For a secondary side impedance defined
by
–
–Z = V2
2 –
I2
(1.1.6)
the input impedance can be written as
N1 –
–
V2
–Z = V1 = N2
1 –
N2 –
I1
N1 I 2
N1 
= N  2 –Z 2
2
(1.1.7)
which demonstrates that impedances are transformed by the square of the turns ratio when viewed on the
opposite side of a transformer. This property is often used in situations where "impedance matching" is
desired and is also very useful in analytically manipulating circuits containing transformers to reduce
circuit complexity for calculations.
March, 2007
3
Introduction to Magnetic Circuits and Transformers
1.1.1 Example - Ideal Transformer Model
To illustrate the application of the ideal transformer model and especially determination of the
correct signs in the equations, consider the three winding transformer shown in Fig. 1.1.3. In using the
model the first step is to select the reference directions for all of the currents and voltages. This
selection is totally arbitrary but is often made to minimize the number of minus signs which will occur
in the resulting equations. The choices in Fig. 1.1.3 have been made to create minus signs for purposes
of illustration.
.
+
v
N
2
2
i2
.
.
–
–
v1
N1
i1
N3
+
+
i3
v3
–
Fig. 1.1.3 Three Winding Transformer with References Selected
For the voltage references in the figure, Eq 1.1.3 becomes
v1
–N
1
v2
=N
2
v3
=N
3
(1.1.8)
where the minus sign on the v1 / N1 term occurs because the reference on v 1 is opposite to that on v2 and
v3. The ampere turn equation for the current references in the figure is
N1i1 – N2i2 + N3i3 = 0
(1.1.9)
since the direction of i2 is opposite to that of i1 and i3.
1.2 Ideal Autotransformers
Although transformers are often used to conductively decouple circuits as well as to change voltage
levels, a considerable reduction in size is possible if a conductive connection between primary and
secondary is permissible. The size reduction is made possible by the fact that an interconnection
between primary and secondary allows addition or subtraction of the primary and secondary voltages
and currents thus increasing the rating over that of the two winding, conductively decoupled connection.
March, 2007
4
Introduction to Magnetic Circuits and Transformers
As an example, consider the autotransformer connection shown in Fig. 1.2.1. From the diagram in
the figure, the volt-amperes delivered at the input is
N1
N1
VAin = v1(i1 + i2) = v1(i1 + N i1) = v1i1 (1+ N )
2
(1.2.1)
2
while that at the output is
N1
N1
VAout = i2(v1 + v2) = i2(N v2+ v2) = v2i2 (1+ N )
2
.
+
v
N
2
i1+ i2
2
+
i2
v1 + v
.
–
+
Source
(1.2.2)
2
v1
N1
2
Load
i1
–
–
Fig 1.2.1 Two Winding Transformer Used As An Autotransformer
As is required the input and output volt-amperes are equal since v 1i1 = v2i2 and the allowable rating of
the autotransformer compared to the two winding transformer is
VAA
VAT =
N1
v1i1 (1+ N )
2
v1i1
N1
= 1+ N
2
(1.2.3)
The amount of increase in rating depends on the turn ratio N1 /N 2 of the original two winding
transformer with a large ratio giving a large increase. The voltage ratio of the autotransformer is
v1 + v 2
=
v1
N2
v1 + N v1
1
v1
N2
= 1+ N
1
(1.2.4)
so that a large rating increase corresponds to a small ratio of output to input voltage in the
autotransformer. Thus, whenever a small change in voltage level is needed, an autotransformer
connection should be considered since it results in a much smaller size magnetic device. It is often
argued that the increase in rating occurs because a portion of the transferred power is conductively
transferred and in fact this is the case since the VA which are actually magnetically transferred at full
March, 2007
5
Introduction to Magnetic Circuits and Transformers
power are exactly equal to the two winding transformer rating. Probably the most commonly used
autotransformer is the "Variac" used in most laboratories as a variable voltage ac supply.
1.3 Transformer Resistances and Reactances
While it is possible to design transformers which function very nearly as ideal transformers in
specific applications, there are always parasitic effects which become apparent at the extremes of the
operating envelope or are allowed to become significant for size, cost or other design related reasons.
These parasitic effects are primarily associated with the three assumptions stated earlier and repeated
here for convenience.
Ideal transformer assumptions:
1) the resistances of the coils are negligible.
2) the flux is entirely confined to the core and thus totally links both windings.
3) the core requires no MMF to support flux (infinite permeability) and has
negligible core loss.
The principal transformer parasitics will now be described and incorporated into a more complete
transformer equivalent circuit model.
Winding Resistance
While the resistances of the windings can be kept small by using appropriate size wire for a specific
application, the resistance can never be made zero. Typically the IR drop at full current is kept less than
1 or 2% of rated voltage and often less than this in large transformers (scaling relations indicate that the
resistance and pu resistance inherently decrease as a transformer is made larger).
To incorporate the winding resistances into a transformer model it is only necessary to connect
appropriate resistors in series with the primary and secondary windings of the ideal transformer as
shown in Fig.1.3.1.
R2
R1
Ideal
+
+
+
+
i
2
i1
v
e
e
v
. .
1
–
1
2
–
–
N1
N
2
–
2
Fig. 1.3.1 Transformer Equivalent Circuit Showing Winding Resistances
March, 2007
6
Introduction to Magnetic Circuits and Transformers
Winding Leakage Inductance
The second assumption which states that all of the flux links every winding is also never totally true
because of the spatially distributed nature of the magnetic flux. Conceptually, one can divide the flux
into main or mutual flux and leakage flux as illustrated in Fig. 1.3.2 in which the space between the
windings where the leakage flux exists has been exaggerated. The ideal transformer relations then apply
to the mutual flux part of the total flux and the leakage flux is treated as a parasitic. The voltage
associated with the leakage flux subtracts from the input voltage in the same way as the IR drop and
reduces the voltage applied to the ideal transformer. The relations are
φ1 = φl + φm
(1.3.1)
where φl is the leakage flux and φm is the mutual flux as shown in the center post of Fig 1.3.2. The total
voltage produced by φ1 is
dφl
dφ1
dφm
v1 = N1 dt = N1 dt + N1 dt = e1l + e1
(1.3.2)
Main (or Mutual) Flux
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Leakage Flux
Fig. 1.3.2 Concept of Main (or Mutual) Flux and Leakage Flux
March, 2007
7
Introduction to Magnetic Circuits and Transformers
where e 1l is the voltage produced by the leakage flux in the primary winding. The voltage e1 is
produced by the mutual flux in the primary winding and is the voltage applied to the ideal transformer
portion of the model in Fig. 1.3.1.
By definition the leakage flux is that flux that links one winding but not the second winding.
Although often represented as having components associated with each winding individually, the
magnetic structure of a transformer is such that it can only realistically be defined by reference to both
windings simultaneously, The leakage flux passes through the air space occupied by the windings and
is produced by the combination of the MMF's N1i1 and N2i2 as illustrated in Fig 1.3.3. As suggested by
the dashed Amperes Law paths in the figure, the MMF driving the leakage flux is provided by the
winding currents, starting with zero MMF at the center post iron, building up in an approximately linear
fashion to N1i1 at the interwinding space and then dropping back to zero across the secondary winding
as a result of the ampere turn balance N1i1 = N2i2. It is apparent from the figure that the leakage flux
passing between the two windings links the winding closest to the center post (considered to be the
primary for this discussion) but does not link the outer winding.
Main (or Mutual) Flux
Leakage Flux
.
.
.
.
.
.
.
.
N1I1
.
.
.
.
.
.
.
.
.
.
.
.
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Sample Ampere’s Law Paths
for Evaluation of MMF
Creating Leakage Flux
MMF Distribution Creating Leakage Flux
Fig. 1.3.3 Leakage Flux Paths and MMF Distribution Creating the Leakage Flux
March, 2007
8
Introduction to Magnetic Circuits and Transformers
Because a large portion of the leakage path length is in air and because the MMF driving the
leakage is N1 i1 , the primary leakage flux is for practical purposes a linear function of the primary
current i1, which allows writing the leakage voltage flux as
φ1l = P l N1i1
(1.3.3)
where Pl is the permeance of the leakage path. The leakage voltage e1l can then be expressed as
dφ1l
dN1P li1
di1
di1
= (N1)2P l dt = L1l dt
e1l = N1 dt = N1 dt
(1.3.4)
where L 1l is the leakage inductance referred to the primary. A similar development can be carried out
for the secondary leading to the leakage inductance referred to the secondary. The only difference in
the two is the turns
L1l = (N1)2P l
L2l = (N2)2P l
(1.3.4)
which can also be interpreted as referring the leakage reactance through the ideal transformer in the
circuit model.
R2
R1
L 1l
Ideal
+
+
+
+
i
2
i1
v
e
e
v
. .
1
–
1
2
–
–
N1
N
2
–
2
Leakage Referred to Primary
L 2l
R1
+
+
v1
–
R2
Ideal
i1
. .
+
e
e1
–
+
i2
2
–
N1
N
v
2
–
2
Leakage Referred to Secondary
Fig. 1.3.4 Transformer Equivalent Circuit Showing Resistances and
Leakage Reactances
March, 2007
9
Introduction to Magnetic Circuits and Transformers
The parasitic resistance and leakage flux of a real transformer are thus represented by series
resistances and inductances connected in series with an ideal transformer. The voltages which appear
across these series elements subtract from the input voltage and thus alter the actual voltage ratio of the
transformer in comparison to the ideal value equal to the turns ratio. In a well designed transformer the
departure from the ideal is small under normal conditions. In cases of operation at the extremes of
possible operation, for example at short circuit on the secondary, the parasitic resistance and leakage
inductance are the whole story and they determine the amount of short circuit current.
It is often convenient to shift all the resistance and leakage inductance to one side of the transformer
using the impedance relation in Eq. 1.1.7. If this is done by transferring the secondary values to the
primary, the result is
N1
Req1 = R1 + N  2 R2
(1.3.5)
Leq1 = L1l
(1.3.6)
2
Fig.1.3.5 illustrates the resulting simplified circuit.
Req
L eq1
1
+
+
v1
Ideal
i1
–
. .
e
e1
–
i2
2
–
N1
N
+
+
v
2
–
2
Fig. 1.3.5 Simplified Equivalent Circuit with all Resistance and Leakage
Inductance Referred to Primary
Magnetizing Inductance and Core Loss
The remaining principal parasitic is the influence of the large but finite permeability of the core and
the losses caused by the ac core flux. The finite permeability modifies Eq.1.14, repeated here for
convenience,
March, 2007
10
Introduction to Magnetic Circuits and Transformers
N1i1 – N2i2 = Hiron liron = 0
(1.1.4)
in that Hiron is no longer zero. As a result the sum of the ampere turns is no longer exactly zero; the
ampere turns of the winding supplied by the source must be a bit larger than the second winding to
supply the required magnetizing MMF. This is conveniently modeled by defining an exciting current
i1ex which supplies the required core MMF and losses according to the relation
N1i1ex = Hiron liron + loss component
(1.3.7)
i1 = i1id + i1ex
(1.3.8)
with
With these definitions, Eq. 1.1.4 without the (= 0) becomes
N1 (i1id + i1ex ) – N2i2 = Hiron liron + loss component
and using Eq 1.3.7 results in
N1i1id – N2i2 = 0
(1.3.9)
The concept is illustrated in Fig.1.3.6. The primary current is viewed as having two components; i1ex
which supplies the necessary MMF and power to create the core flux and i1id which provides the useful
interaction with the secondary winding following the ideal transformer laws.
i1
i 1id
+
+
v1
–
i 1ex
i2
Ideal
. .
e1
–
+
+
e
v
2
–
N1
N
2
–
2
Fig. 1.3.6 Equivalent Circuit Showing Exciting Current Resulting from Finite
Core Permeability and Core Losses
The remaining task is to determine the nature of i1ex and means of representing it in terms of a
simple circuit model. Two limiting cases are of value in understanding the nature of the exciting
current. First, consider the case of finite, constant core permeability and zero core loss. In this case the
core is easily modeled as having a constant permeance and the core flux is then given by
March, 2007
11
Introduction to Magnetic Circuits and Transformers
µcAc
φm = l
N1i1ex =P cN1i1ex
c
(1.3.10)
which leads to the magnetizing inductance L m
N1 φm
Lm = i
= ( N1) 2 P c
1ex
(1.3.11)
Second, consider the case where the core is infinitely permeable (so L m is infinite) but there are eddy
current losses in the core. The eddy currents are created by the voltage produced in the core by the time
changing core flux - exactly the same process that creates the voltages in the transformer windings. A
resistive load on a winding will therefore absorb power in a very similar fashion as the eddy current
losses. It is therefore reasonable to model the eddy current loss as a resistor connected such that it is
exposed to a voltage generated by the core flux.
These two limiting cases lead to the circuit shown in Fig. 1.3.7, which is also the most common form
of representation of the excitation and core loss requirements of a real transformer. While strictly
speaking the model is only valid for constant permeability and for eddy current losses, it is used as an
approximation for the more realistic situations where saturation creates variable permeability and where
the core loss includes hysteresis loss.
i2
i1
i 1id
Ideal
+
+
+
+
i
. .
1ex
i 1c
–
e
e1
v1
2
v
2
i 1m
–
–
N1
N
–
2
Fig. 1.3.7 Equivalent Circuit Showing Magnetizing and Core Loss Currents
To demonstrate that the circuit of Fig. 1.3.7 is a reasonable model for a system with magnetic
hysteresis, consider the flux-current characteristics shown in Fig. 1.3.8. As shown in the figure, the total
flux-current characteristic for any steady state flux cycle can be separated into a roughly rectangular
hysteresis loop and the associated magnetizing current curve. Focusing on the hysteresis loop, note that
March, 2007
12
Introduction to Magnetic Circuits and Transformers
λ
λ
i
λ
i
i
Fig. 1.3.8 Separation of Magnetic Hysteresis and Magnetizing Current
λ
λ
i
t
i
t
Fig. 1.3.9 Waveform of Magnetizing Current with Saturated Core
March, 2007
13
Introduction to Magnetic Circuits and Transformers
whenever the flux is increasing the current required is positive (in the case shown, a positive constant).
Since from Faraday's Law an increasing flux requires a positive voltage, both the voltage and current are
positive and thus "in phase" as in a resistor. For a material with a true rectangular hysteresis loop the
current is a rectangular wave in time which is in phase with the voltage wave (and independent of the
voltage waveform).
For realistic designs the magnetizing current curve almost always shows some saturation and this
results in a magnetizing current which is non-sinusoidal when the applied voltage is sinusoidal. The
relationships are illustrated in Fig. 1.3.7. Here it is assumed that the IR drop is negligible and hence the
sinusoidal voltage results in a sinusoidal flux linkage. However the saturation non linearity of the core
maps this sinusoidal flux linkage into a magnetizing current which has a peak in the center of the flux
wave and thus near the zero crossings of the voltage wave. Note that it is important to keep this nonsinusoidal current small enough so the resulting IR drop is small compared to the input voltage or flux
waveform distortion (and hence output voltage distortion) will occur.
1.4 Transformer Equivalent Circuit
Combining the concept of leakage flux and inductance depicted in Fig. 1.3.4 and that of main flux and
magnetizing inductance depicted in Fig. 1.3.7 yields the generally accepted transformer equivalent
circuit shown in Fig. 1.4.1.
L 1l = L eq1
R1
+
i1
i 1ex
i 1id
v1
+
. .
Rm L m
+
e
e1
i 1c
–
R2
Ideal
i 1m
–
2
–
N1
N
+
i2
v
2
–
2
Fig 1.4.1 Transformer Equivalent Circuit
Because of the quality of most well designed transformers (i.e. small R1 , R2 , L1l and large Rm and
Lm) it is seldom necessary to use the full circuit in the form shown in Fig 1.4.1. For example:
March, 2007
14
Introduction to Magnetic Circuits and Transformers
1) Rm and L m can usually be neglected except for operation at light load, when efficiency is
being evaluated or if greater than rated voltage is applied.
Req
L 1l = L eq1
1
Ideal
+
+
v1
i1
–
. .
L 1l
e
e1
–
+
+
i2
–
–
N1
N
v
2
2
2
Fig 1.4.2 Transformer Equivalent Circuit with Rm and Xm Neglected
2) In large transformers or high frequency transformers the resistances are typically small
compared to ωL1l and can be neglected along with Rm and Lm. The equivalent circuit then
reduces to a single reactance equal to ωL 1l or ωL 2l depending on which side of the ideal
transformer is modeled.
L 1l = L eq1
+
+
v1
–
Ideal
i1
. .
e
e1
–
+
+
i2
2
–
N1
N
v
2
–
2
Fig 1.4.3 Transformer Equivalent Circuit with Req, Rm and Xm Neglected
3) Often the reactance X1l or X2l is small compared to other impedances in the circuit and can
be neglected. The transformer equivalent circuit then becomes that of an ideal transformer.
Ideal
+
+
+
+
i2
i1
v
e
e
v
. .
1
–
1
2
–
–
N1
N
2
–
2
Fig 1.4.4 Ideal Transformer - All Parasitics Neglected
1.5 Transformer Core Materials and Core Construction
Historically, electric motors, transformers and inductors have been constructed from magnetic
steels usually in the form of thin laminations, electrical conductors (either copper or aluminum),
March, 2007
15
Introduction to Magnetic Circuits and Transformers
insulation for the conductors and slots, high tensile strength steel for shafts and steel or copper alloys for
bearings. The laminations used in most general purpose motors, transformers and inductors have been
“common iron” or low carbon steel. Although low in cost, this material typically produces devices of
only modest efficiency. More recently, high efficiency designs often feature higher quality silicon steels
at a correspondingly higher cost. The percent of silicon in the steel has a beneficial effect in reducing
losses in the steel but at the same time tends to reduce the saturation flux density. The percent of silicon
in motor steels typically ranges from 1% to 3.25%. The corresponding losses range from 0.6 watt per
pound of core for the 3.25% steel to 1.0 watt per pound for the 1% silicon steel at a flux density of
15,000 gauss (1.5 tesla). Nickel alloys, such as permalloy, have low losses but are very expensive and
have low saturation flux density. The cobalt alloys such as Supermendur (49% iron, 49% cobalt and 2%
vanadium) have peak flux densities over 20,000 gauss, but are also very expensive and have higher
losses.
When the magnetic structure is assembled by means of stacking laminations punched from thin sheet
material, the volume occupied by the stacked laminations does not truly represent the volume of iron
that supports the magnetic flux. A region whose permeability is that of air exists between the
laminations because of the presence of irregularities in the laminations or due to a thin coat of insulating
varnish applied to avoid circulating current flow between laminations (eddy currents). In order to allow
for this effect, the effective cross- sectional area of iron is equal to the cross-sectional area of the stack
times a factor called the stacking factor. This factor, defined as the ratio of the cross sectional area of the
actual iron to the cross sectional area of the stack, ranges between about 0.95 and 0.90 for lamination
thickness between 0.025 inch and 0.014 inch (25 and 14 mil) respectively. For thinner laminations, for
example 1 mil to 5 mil thick, the stacking factor can be in the range of 0.4 to 0.75. Thinner laminations
than 14 mil are generally not used at 60 hz unless iron loss is a severe problem but are common at higher
frequencies, for example in aircraft generators or higher switching frequency power supplies.
A new group of alloys has already been developed grouped under the generic title of amorphous
metal alloys. These materials represent a new state of matter for electromagnetic materials, the so called
amorphous or non-crystalline state. Ordinary window glass is a typical example of an amorphous
material. Some of these new amorphous alloys have magnetic properties which surpass the properties of
conventional alloys. Thus, they appear to be a potentially useful new class of soft magnetic material.
These alloys contain about 80% ferritic elements such as iron, nickel and cobalt, and 20% glasseous
elements such a silicon, phosphorous, boron, and carbon. A good example of an amorphous alloy
having 80% iron and 20% boron by atomic weight is Fe80B 20 (Allied Chemical’s Metglass). Major
advantages of amorphous metal include low cost, very low core loss ( one fifth that of the best silicon
steels), low annealing temperature and high tensile strength. Unfortunately, this new material has not
yet been used on a large scale at typical power line frequencies because the high tensile strength also
March, 2007
16
Introduction to Magnetic Circuits and Transformers
makes the material difficult to punch or otherwise utilize in conventional structures. Also, amorphous
materials are presently only available in thicknesses of 1 to 2 mils (0.001” to 0.002”) which results in a
poor stacking factor and creates problems during assembly. Tape wound cores for applications up to 10
to 20 khz are available and represent an important alternative at these frequencies.
An important class of materials for higher frequency devices (from low audio frequencies to several
hundred megahertz) are the soft ferrites. Ferrites are ceramic materials composed of various oxides with
iron oxide as the main ingredient. They offer low loss combined with high permeability, very high
resistivity (virtually all of the core loss is hysteresis loss) and are easily produced in a wide range of
shapes. Disadvantages include limited flux densities, brittleness and low thermal conductivity. A wide
variety of material types exist to cover the very large frequency range served by ferrites. Ferrite is very
often the only realistic choice in high frequency applications and the core selection process is essentially
one of finding the best ferrite type for the specific task.
Because of the very high electrical resistivity the losses in ferrites at typical operating frequencies
are almost entirely hysteresis losses. As a result the loss is linearly dependent on frequency and virtually
independent of the waveform of the flux. These statements follow from the hysteresis energy loss
dependence on the area of the hysteresis loop and thus on the number of loops per second for the power
loss. Waveform independence follows from the fact that the rate at which portions of the loop are
traversed does not matter; only the area of the total loop is significant. There is an exception to the
waveform independence for loops containing a minor loop as shown in Fig. 1.5.1. Creation of a minor
loop requires that the direction of flux change be reversed and subsequently rereversed. This in turn
requires that the polarity of the induced voltage change sign (have multiple zero crossings) as illustrated
in Fig. 1.5.1. The hysteresis loss is generally increased by the minor loop since part of the area of the
loop is covered twice.
Powdered materials provide another important class of core materials, especially for inductors.
These cores generally have low but highly controlled relative permeability in the range of ten to a few
hundred. Typical materials include molypermalloy, nickel-iron and iron-aluminum-silicon. In general
these materials provide the equivalent of a distributed air gap and can provide significant improvement
in performance compared to a conventional core plus air gap design.
March, 2007
17
Introduction to Magnetic Circuits and Transformers
B
Minor Loop
H
Negative Voltage
Creating Minor Loop
v(t)
t
Fig.1.5.1 Illustration of Creation of a Minor Loop and Associated Increase of Hysteresis Loss
March, 2007
18