Download 1 = A

DYNAMICAL SYMMETRIES IN NANOPHYSICS
K. Kikoin
(Tel-Aviv University)
PLAN
I.
• Group theory in quantum mechanics. Basic definitions .
• Symmetry of Hamiltonian.
• Hidden symmetry of Hamiltonian
• Dynamical symmetries of multiplet
II.
• Nanoobjects: single-electron tunneling through quantum dots and molecules
• Dynamical symmetries of few-electron systems
• Kondo effect and Kondo-regime in single electron tunneling
• Kondo exotics
Galitsky-2010
1
OMNIPRESENT GROUP THEORY
Set of elements E,A,B,C,… N plus multiplication rule
1.
2.
3.
4.
Closeness: Product of two elements AB=C in the set belongs to the set
Associativity: (AB)C = A(BC)
Existence of a unite element: EA = AE = A
Existence of inverse elements: AA-1 = A-1A = E for any A
The set without (4) forms semigroup
Tutorial example:
Multiplication table:
E
J
K
L
M
N
E J
K L M N
E
J
K
L
M N
J
K
E
N
L
M
K
E
J
M N
L
L
M N
E
J
K
M N
L
K
E
J
N
M J
K
E
L
Galitsky-2010
Isomorphism:
= Group D3 of discrete rotations
= Permutation group P123
1
3
2
2
GROUP THEORY IN QUANTUM MECHANICS
Ingredients:
Noether theorem: Any differentiable symmetry of the action has a corresponding conservation law.
Homogeneity in time – energy conservation
Homogeneity in space: – momentum conservation
Isotropy in space: – angular momentum conservation
Wigner theorem:
The wave functions belonging to a given eigen energy E
transform along a representation of the group G of the
Schroedinger equation
Hψ({x}) = Eψ({x})
HRψ({x}) = ERψ({x}).
δr
Infinitesimal operators as generators of Lie algebras
These operators perform infinitesimal translations and rotations
in space time and form the basis if irreducible representations
of continuous Lie groups. Example: rotations on a 3D sphere
Laplacian Δ is invariant under transformations in Euclidean space. In case of rotation group SO(3)
we deal with
invariant under rotations on the sphere.
Galitsky-2010
3
These operator form closed Lie algebra o(3)
J2 is the Casimir operator, which commutes with unit operator. In general case several
Casimir operators may be constructed from group generators. Usually Casimir operators
explicitly enter the Hamiltonian. In particular, one may use J2 instead of Δ .
In some special cases Casimir operators do not enter the Hamiltonian. This is the sign of
hidden symmetry
Example: electron in a Coulomb potential ~ 1/r .
It was noticed (W. Pauli, 1927, V.A. Fock, 1935) that the Schroedinger equation with this
potential is in fact 4-dimensional (in {p,ε}-space) . As a result three more generators may be
introduced which form a Runge-Lenz vector (L=iħI)
Two last equation define two Casimir operators for a group of 4D rotations SO(4)
in this specific potential. But the operator N does not enter the Hamiltonian!
Galitsky-2010
4
SO(4) group of rotations on 4D sphere – example of semisimple group.
Let us add one more dimension to our Euclidean 3D world. Time t may play part of his
additional coordinate. To describe rotations on 4D sphere one needs three more infinitesimal
operators
(*)
These 6 operators form closed so(4) algebra
Two Casimir operators are
A linear transformation converts (*) into another basis
with commutation relations
Triads with commutation relations of this type form ideals of the o(4) algebra. Algebra possessing
non-Abelian ideal is qualified as a semisimple algebra.
Two Casimir operators in these terms are
Galitsky-2010
5
Now we are prepared to discussion of
dynamical symmetries
Representation theory in quantum mechanics implies symmetry operations on matrices. Each symmetry
group is realized in some basis forming the irreducible representations. In case of rotation group SO(3)
these are spherical functions Ylm ( φ,θ). Wigner theorem in these terms means that the matrix
representation of Schroedinger equation has a block-diagonal form
Δl=1 Δl=2
l=2
…
s
l=1
Question:
what about
off-diagonal
blocks ?
p
d
…
l – operators have nonzero matrix
elements only within a given block.
Each block corresponds to the eigen
energy El
…
s
l=0
…
p
d
…
To find the answer let us return to the physical realization
of SO(4) symmetry, namely to rigid quantum rotator
Galitsky-2010
6
z’
z
α
Angular coordinates contain three angles: (φ,θ,α). The latter angle describes precession
of rotator axis z’ around cartesian axis z in 3D space. This angle play the same part as
the time t in definition of the operator M . Thus, effective dimension of phase space
for the states of rigid rotation is D=4.
Basis of representations of SO(4) group in angular coordinates is given by
hyperspherical functions
Ladder operators Mi act on the spherical functions with given n in the following way:
(cl and al are some constants). Thus M-operators unlike L-operators raise (lower) orbital index l , and
the set of operators L, M involves both diagonal blocks and off-diagonal blocks with Δl = 1 in the
Hamiltonian matrix.
One says that the group SO(4) realizes the dynamical symmetry of rigid rotator.
Generators of dynamical symmetry group describes transitions between the levels of the
supermultiplet, i.e., the levels belonging to different irreducible representations and different
eigenstates of the Hamiltonian.
Galitsky-2010
7
SO(4) symmetry in spin systems: singlet-triplet multiplet formed by two electrons
4 states form spinor of 4th rank
1
s
0
-1
R
S=1
s
S=0
These operators were invented by J. Hubbard
T
…
Spin 1 operators S generate o(3) algebra and generators Sz, S+, S- describe rotations on a 3D sphere
in spin space. Adding vector R (allowing singlet-triplet transitions) we extend the rotation group from
SO(3) to SO(4).
Galitsky-2010
8
Commutation relations are the same as for operators L and M in quantum rotator problem.
Casimir operators:
Electron spins are not independent in SO(4) group: they are constrained by the second Casimir operator.
When the dynamical symmetry becomes actual?
In stationary state spin is conserved as well as angular momentum, and we are satisfied with
conventional (Wigner’s) symmetry of the Hamiltonian.
Dynamical symmetry is activated in interaction with external fields (electromagnetic field etc)
and in interaction with environment.
The latter possibility is realized in nanophysics.
Galitsky-2010
9
One more physical example: SO(5) algebra for Wannier excitons
for three vectors S,R,M and scalar A
Singlet GS
T-exciton
S-Exciton
S = 2 X 10 +X 0− 1 ; S z =X 11− X − 1− 1
R = 2 X 1S− X S− 1 ; R z = − X 0S +X S0
+
1
E E
1 z
0
E
E
0
M
=
2
X
X
;
M
=
X
+
X
(
)
(
)
A
M
S
E E
S
A
=
i
X
X
(
)
Commutation relations
1
s
0
R
-1
[Si,Sk] = ie ijkSk, [Si,Rk] = ie ijkSk, [Ri,Rk] = ie ijkSk,
[Si,Mk] = ie ijkMk, [Mi,Mk] = ie ijkSk, [Ri,Mk] = iAΔ ik
Kinematics: three Casimir operators
S2 + R2 + M2 + A2 = 4
Galitsky-2010
10
This construction may be generalized for higher groups SO(n)
Group generators are combined in vectors (V) and
scalars (A)
Multiplet consists of singlets (S) and triplets (T)
In some physical problems group generators form tensors (e.g. spin systems with uniaxial magnetic
anistropy). In the latter case the dynamical symmetry SU(3) is realized by one vector and one
tensor.
Galitsky-2010
11
A little more about SU(n) groups in a context of dynamical symmetries
Mathematically SU(n) is a group of unitary matrices of n-th rank. In nanophysics one frequently
deals with the groups SU(3) and SU(4).
SU(3) group describes all interlevel transitions in a three-level system.
Its generators are so called Gell-Mann matrices which are the
generalization of su(2) Pauli matrices σ. The GM matrices may be
combined in three triads:
3x3
Only eight of these matrices may be used
as linearly independent generators of
SU(3) group.
σ+
σ-
σ3
Galitsky-2010
12
The simplest physical realization of SU(4) symmetry group is a two-well potential with one electron inside.
Electron is characterized by spin with two projections (up and down)
and its position in the wells (left and right). Both quantum numbers are
realized by means of Pauli matrices σ and τ (spin and pseudospin, resp.).
15 generators of SU(4) group are constructed as
(*)
These generators describe all positions of electron in the potential relief and all possible transitions
between the quantum states. If one is interested only in spin conserving transitions between two
wells, but the spin flips in a given well are allowed, the matrix (*) reduces to
In this case the dynamical symmetry is reduced:
Now we are well equipped for investigation of dynamical symmetries in quantum
dots and related nano-objects.
Galitsky-2010
13
Planar quantum dots
Galitsky-2010
14
Coulomb blockade due to noticeable capacitive energy of QD.
Galitsky-2010
15
Coulomb windows diagram: tunnel conductance G as a function of eV, Vg
odd
even
odd
even
G = dI/dV
Single electron tunneling
Galitsky-2010
16
In a Coulomb window direct tunneling is suppressed by Coulomb blockade and only cotunneling
processes are possible. These processes are accompanied by creation of electron- hole pairs
either in the same lead or in different leads. The latter process is responsible for charge transport.
The electron spin is not conserved in cotunneling processes.
σ’
σ
(a)
σ
(b)
σ’
(c)
Galitsky-2010
(d)
17
CONVENTIONAL KONDO COTUNNELING:
theory
Zero energy spin reversal peak ~δ(0)
develops into resonance due to dynamical
screening by electron-hole pairs
from continuum (Kondo cloud)
N=1
E+U
TK ~ D0 exp(-1/2νJ(0))
E
Kondo Hamiltonian
H = J (S s)
S=1/2
Galitsky-2010
18
How does Kondo effect in quantum dots looks experimentally:
G = dI/dV – tunneling conductance
a
Galitsky-2010
b
19
KONDO SCREENING
Undersreened
N
N-1
reduced spin+
free electrons
screened
N
N-1
Kondo singlet +
free electrons (FL)
overscreened (two-channel)
N
N
N-1
N-1
...
non-Fermi liquid (NFL)
Magnetic response:
1/T + const
const - (T/TK)2
Galitsky-2010
Ta
20
Kondo cotunnelling through DQD: N=2
Two electrons always form spin Singlet and spin Triplet
1
S
0 T
R
T
S
Generalized Kondo Hamiltonian
H= J1 (S s) + J2 (R s)
S=1 plus singlet
-1
Usually ground state is S,
but the S/T level crossing
is possible under certain conditions.
Unconventional features of
Kondo tunneling may be observed
when
ΔTS ~ T K Δ TS
Galitsky-2010
21
General view on emergence of dynamical symmetries
C
O
N
T
I
N
U
U
M
δE
Flow RG?
Galitsky-2010
22
Dynamical symmetry alters (or arises) in the course of contraction of the energy scale δE.
Let us look how does this mechanism work in case of Kondo effect.
Even conventional Kondo effect (N=1) may be described in terms of dynamical symmetries.
Basic Hamiltonian is that of the Anderson model describing cotunneling through a quantum dot.
E
2D0
εd +U
0
εd
The Renormalization Group procedure is applied to this Hamiltonian.
In the course of energy scale reduction the dot level εd shifts ~ ln (D0 -D).
(a)
When the renormalized level crosses the boundary D the first stage of
RG procedure terminates. We are now in a regime of localized spin
described by the Kondo Hamiltonian H = J (S s) with J ~ W2/ εd , and
in the second stage of scaling procedure the coupling constant J is renormalized.
The scaling equation reads
with
D0
D
0
(b)
Its solution is
J(T) turns to infinity (reaches the stable fixed point) at T=TK
Galitsky-2010
23
The same procedure in terms of dynamical symmetries:
Kinematic scheme of possible spin and charge transitions
E
Symmetric Hubbard parabola
N= 0
1
2
0, 2
1
0
0
Spin
Charge
All these transitions in 4-level system are described by generators of SU(4) group.
This is the basic symmetry of Hubbard atom with varying N =0,1,2
Galitsky-2010
24
If E(2) – E(1) >> E(0) – E(1), the doubly occupied state
is first to be integrated out in the process if RG procedure
and we remain with SU(3) symmetry
0
E
N= 0
Asymmetric Hubbard parabola
1
2
1
0
Spin
Charge
Transition from Anderson model to exchange model means elimination of empty state and
eventually we come to the scheme containing only spin states and describing SU(2) Kondo effect.
Galitsky-2010
25
This construction is only rephrasing of the well known procedure which means not too much from
practical point of view, but dynamical symmetries are deeply involved in
Kondo effect at even occupation .
Within the energy interval δE ~ ΔTS ~ T K Δ TS
the exchange (cotunneling) Hamiltonian is
H= J1 (S s) + J2 (R s)
and both parameters J1 and J2 are subject to RG renormalization. The system of scaling flow equations
Solution of this system gives for TK as a
function of exchange gap
0
- ΔTS
Maximum TK is reached at ΔTS = 0, where the singlet and triplet states are degenerate. The sign and
the magnitude of this gap may be controlled by the gate voltage vg , so this effect is experimentally
checkable.
Galitsky-2010
26
Magnetic field induced (!) Kondo effect
-1
ET
0
S
ES
1
B
R = 2 X 1S , R z =X 11− X SS
H Kondo =J R⋅ s
It was the first example of Kondo effect due to
dynamical symmetry of DQD
D. Kobden et al, Nature, 408, 342 (2000)
M. Pustilnik, Y. Avishai & KK, PRL, 84, 1756 (2000)
Galitsky-2010
27
Intermezzo: other types of quantum dots.
“Fock – Darwin” atoms with cylindrical symmetry
Vertical dots with parabolic
confinement potential
l=
-2
-1
●●
0
+1 +2
n
●●
●●
2
●●
●●
1
0
●●
Galitsky-2010
28
“Periodic table” for vertical dots
Transition between the oscillator levels are described
by SO(2,1) two-dimensional Lorenz group.
Galitsky-2010
29
Endofullerene
Fullerene quantum dots
Nanotube quantum dots
Galitsky-2010
30
Double and triple quantum dots
Ring-like dots
Self-assembled semiconductor quantum dots
Excitonic atom
Galitsky-2010
31
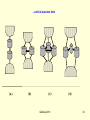
Basic configurations of double quantum dots
s
W
V
W
(a)
r
l
d
(b)
(c)
Galitsky-2010
(d)
32
… triple quantum dots
(a)
(b)
(c)
(d)
W
V
(e)
(f)
(g)
Galitsky-2010
(h)
(i)
33
…vertical quantum dots
(a)
(b)
(c)
Galitsky-2010
(d)
34
Kondo effect and Aharonov – Bohm interference in “which path” geometry
Ф
Two paths have different chirality when turning the magnetic
flux from the left and from the right. As a result two partial
waves meet in the dot 3 with phase difference
W
V
The interference effect ~ 1 –
may partially or completele suppress Kondo tunneling
Galitsky-2010
35
Exotic Kondo effect where spin and charge variables change their role.
Triple quantum dot in parallel configuration. Central dot is smaller than side dots, and the Coulomb
blockade is stronger.
εc + Qc
s
Qic
l
εi + Qic
r
c
εi
W
d
εc
Galitsky-2010
36
Two electrons, singlet ground state with S = 0
Spin reversal is impossible in a singlet state, but position of the level have changed (pseudospin reversal).
This is possible realization of two-channel Kondo effect, where spin enumerates channels and
position plays part of spin!
Galitsky-2010
37
CONCLUDING REMARKS
In artificial nanoobjects various types of dynamical symmetries
may be realized and used in practical (?) applications
Y. Avishai (Israel)
Y. Oreg (Israel)
M. Kiselev (Italy)
T. Kuzmenko (Israel)
R. Shekhter (Sweden)
M. Wegewijs (Germany)
Galitsky-2010
38