Download form Given matrix The determinant is indicated by

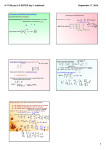
DETERMINANTS
Dr. Shildneck
Fall, 2015
What is a DETERMINANT?
▪ The determinant of a matrix is a NUMBER that is
associated to that matrix that helps us to determine
things about that matrix.
▪ Only SQUARE matrices have determinants.
▪ You will be required to find determinants of 2x2
and 3x3 determinants by hand.
NOTATIONS for DETERMINANTS
A determinant might be asked for in a couple of
different ways.
▪ “DET” form
▪ “Bar” form
“DET” form
Given matrix
1
A=
3
2
4
The determinant is indicated by
1
2
Det(A) or Det
3 4
“BAR” form
Given matrix
1
A=
3
2
4
The determinant is also indicated by
|A|
or
1
3
2
4
The DETERMINANT of a 2x2 Matrix
▪ To find the determinant of a 2x2 matrix use the
“Down – Up” Diagonal Method.
𝑎
det
𝑐
𝑏 = ad - cb
𝑑
The DETERMINANT of a 2x2 Matrix
Find the value of the determinant
1 2
det
3 4
The DETERMINANT of a 2x2 Matrix
Find the value of the determinant
7
8
−3
2
The DETERMINANT of a 3x3 Matrix
To find the determinant of a 3x3 matrix
we will use the LATTICE METHOD…
This method ultimately turns into an
augmented version of the “Down – Up”
Diagonal Method.
The LATTICE METHOD
1) Copy the first and second column to the right of the
matrix/determinant.
2) Draw “Down” diagonals under each of the three 3-term
“down” diagonals.
3) Multiply the numbers in each diagonal and add them
together… this is your “DOWN” total.
4) Draw “Up” diagonals under each of the three 3-term “Up”
diagonals.
5) Multiply the numbers in each diagonal and add them
together… this is your “UP” total.
6) Now do “Down minus Up.”
The LATTICE METHOD
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
= ( aei +bfg +cdh ) - ( gec +hfa +idb )
The LATTICE METHOD
2 3 0
1 2 1
4 2 −1
DETERMINANT EQUATIONS
Since Determinants are just numbers, they can be equal to
some value, even if there are variables inside.
To solve a variable equation, just evaluate the determinant
using the processes we have discussed and simplify the
algebraic expression.
Then, set that expression equal to the value of the
determinant and solve for the variable.
The DETERMINANT EQUATION
Find the value of the unknown.
𝑥
1
5
=16
−3