Download Newton`s Laws and His System of the World

PART C
Newton's Laws & His System of the
World
9. Newton's Laws of Motion
10. Rotational Motion
11. Newton’s Law of Universal Gravitation
MAJ. Wasono & Team
Newton's Laws and His System of the World



This subject of the formation of the
three laws of motion and of the law
of gravitation deserves critical
attention.
The whole development of thought
occupied exactly two generations. It
commenced with Galileo and ended
with Newton's Principia; and Newton
was born in the year that Galileo
died.
Also the lives of Descartes and
Huygens fall within the period
occupied by these great terminal
figures.
(A. N. Whitehead, Science
and the Modern World)



As we look into history, it seems that sometimes progress in a
field of learning depended on one person's incisive formulation
of the right problem at the right time. This is so with the
section of mechanics called dynamics, the science that deals
with the effects of forces on moving bodies.
The person was Isaac Newton, and the formulation was that of
the concepts force and mass, expounded in three
interconnected statements that have come to be called
Newton's three laws of motion.
But also, with the help of Newton's law of universal gravitation,
we can solve some of the outstanding problems in astronomy
introduced in Part A. Once we have successfully dealt with
such problems, Newtonian dynamics becomes a powerful tool
for advancing to the next level of understanding the physical
sciences.
Newton's Laws of Motion

Contents :
9.1 Science in the 17th Century












Between the time of Galileo's death and the publication of Isaac Newton's Philosophia
Naturalis Principia Mathematica (1687) lie barely 44 years, yet an amazing change in the
intellectual climate of science has taken place in that brief interval.
The "New Philosophy“ of experimental science is becoming a respected and respectable tool
in the hands of vigorous and inventive investigators; and, on the other, this attitude is
responsible for a gathering storm of inventions, discoveries, and theories.
Covering less than half of the 17th century and only the physical sciences, will show the
justification for the term "the century of genius" :
The work on vacuums and pneumatics by Torricelli, Pascal, von Guericke, Boyle, and
Mariotte;
Descartes‘ great studies on analytical geometry and on optics;
Huygens' work in astronomy and on centripetal force, his perfection of the pendulum clock,
and his book on light;
The establishment of the laws of collisions by Wallis,Wren, and Huygens;
Newton's work on optics, including the interpretation of the solar spectrum, and his
invention of calculus almost simultaneously with Leibniz;
The opening of the famous Greenwich observatory; and
Hooke's work, including that on elasticity.
Science is clearly becoming well defined, strong, and international.
What is behind this sudden blossoming?



One aspect is that both craftsmen and men of leisure and
money begin to turn to science, the one group for
improvement of methods and products and the other for
a new and exciting hobby-as amateurs (in the original
sense, as lovers of the subject).
But availability of money and time, the need for science,
and the presence of interest and organizations do not
alone explain or sustain such a thriving enterprise.
Even more important ingredients are able scientists,
well educated persons, well-formulated problems,
and good mathematical and experimental tools.
9.2 A Short Sketch of Newton's Life





Isaac Newton was born on Christmas day in 1642, in the small village of
Woolsthorpe in Lincolnshire, England.
He was a quiet farm boy who, like young Galileo, loved to build and tinker with
mechanical gadgets and seemed to have a secret liking for mathematics.
Through the fortunate intervention of an uncle he was allowed to go to Trinity
College, Cambridge University, in 1661 (where he appears to have initially enrolled
in the study of mathematics as applied to astrology!).
He proved an eager and excellent student. By 1666, at age 24, he had quietly made
spectacular discoveries in mathematics (binomial theorem, differential calculus),
optics (theory of colors), and mechanics.
Referring to this period, Newton once wrote:
 And the same year I began to think of gravity extending to the orb of the Moon, and . . .
from Kepler's Rule [third law] . . . I deduced that the forces which keep the Planets in
their orbs must [be] reciprocally as the squares of their distances from the centers
about which they revolve: and thereby compared the force requisite to keep the Moon
in her orb with the force of gravity at the surface of the earth, and found them to
answer pretty nearly. All this was in the two plague years of 1665 and 1666, for in those
days I was in the prime of my age for invention, and pIinded Mathematics and
Philosophy more than at any time since.

(quoted in Westfall, Never at Rest)


From his descriptions we may conclude that during those
years of the plague, having left Cambridge for the time to study
in isolation at his home in Woolsthorpe, Newton had
developed a clear idea of the first two laws of motion and of
the formula for centripetal acceleration, although he did not
announce the latter until many years after Huygens' equivalent
statement.
After his return to Cambridge, he did such creditable work
that he followed his teacher as professor of mathematics. He
lectured and contributed papers to the Royal Society, at first
particularly on optics. His Theory of Light and Colors, when
finally published, involved him in so long and bitter a
controversy with rivals that the shy and introspective man
even resolved not to publish anything else.


Newton now concentrated most on an extension of his
early efforts in celestial mechanics the study of planetary
motions as a problem of physics.
In1684 the devoted friend Halley came to ask his advice
in a dispute with Wren and Hooke as to the force that
would have to act on a body executing motion along an
ellipse in accord with Kepler's laws; Newton had some
time before found the rigorous solution to this problem
("and much other matter") . Halley persuaded his
reluctant friend to publish the work, which touched on
one of the most debated and intriguing questions of the
time.



In less than two years of incredible labors the Principia
was ready for the printer; the publication of the volume
(divided into three "Books") in 1687 established Newton
almost at once as one of the greatest thinkers in history.
A few years afterward, Newton, who had always been in
delicate health, appears to have had what we would now
call a nervous breakdown.
On recovering, and for the next 35 years until his death in
1727, he made no major new discoveries, but rounded
out earlier studies on heat and optics, and turned more
and more to writing on theology.
9.3 Newton's Principia

In the original preface to Newton's we find a clear outline:



Since the ancients considered mechanics to be of the greatest
importance in the investigation of nature and science, and since the
moderns have undertaken to reduce the phenomena of nature to
mathematical laws, it has seemed best in this treatise to concentrate on
mathematics as it relates to natural philosophy [we would say "physical
science"] . . .
For the basic problem of philosophy seems to be to discover the forces
of nature from the phenomena of motions and then demonstrate the
other phenomena from these forces. It is to these ends that the general
propositions in Books 1 and 2 are directed, while in Book 3 our
explanation of the system of the world illustrates these propositions. For
in Book 3, by means of propositions demonstrated mathematically in
Books 1 and 2, we derive from celestial phenomena the gravitational
forces by which bodies tend toward the sun and toward the individual
planets.
Then the motions of the planets, the comets, the moon, and the sea
[tides] are deduced from these forces by propositions that are also
mathematical.


What a prospect! The work begins with a set of definitions: in this case,
mass, momentum, inertia, force, and centripetal force. Then follows a
section on absolute and relative space, time, and motion.
Mass

Newton was very successful in using the concept of mass, but less so in
clarifying its meaning. He states that mass or "quantity of matter“ is "the
product of density and bulk" (bulk volume). But what is density? Later on in
the Principia, he defines density as the ratio of "inertia“ to bulk; yet at the
beginning, he had defined inertia as proportional to mass.
=


Thus a modem text or encyclopedia typically states that mass is simply an
undefined concept that cannot be defined in terms of anything more
fundamental, but must be understood operationally as the entity that
relates two observable quantities, force and acceleration. Newton's second
law, to be introduced below, can be regarded as a definition of mass.
What is more important is that Newton clearly established the modem
distinction between mass and weight-the former being an inherent
property of a body, whereas the latter depends on the acceleration due to
gravity at a particular location.

Time. Newton writes:



Absolute, true, and mathematical time, in and of itself and of its own nature,
without relation to anything external, flows uniformly, and by another name is
called duration.
Relative, apparent, and common time, is any sensible and external measure
(precise or imprecise) of duration by means of motion such a measure-for
example, an hour, a day, a month, a year-is commonly used instead of true time.
Space. Newton continues:



Absolute space, of its own nature without reference to anything external, always
remains homogeneous and immovable.
Relative space is any movable measure or dimension of this absolute space; such
a measure or dimension is determined by our senses from the situation of the
space with respect to bodies . . .
Since these parts of space cannot be seen and cannot be distinguished from one
another by our senses, we use sensible [perceptible by the senses] measures in
their stead . . . instead of absolute places and motions we use relative ones, which
is not inappropriate in ordinary human affairs, although in philosophy, abstraction
from the senses is required. For it is possible that there is no body truly at rest
to which places and motions may be referred.



In the introductory section of the Principia, Newton stated his
famous three laws of motion and the principles of composition
of vectors (for example, of forces and of velocities). Book 1 ,
titled "The Motion of Bodies," applies these laws to
problems of interest in theoretical astronomy:
the determination of the orbit described by one body around
another, when they are assumed to interact according to
various force laws, and mathematical theorems concerning the
summation of gravitational forces exerted by different parts of
the same body on another body inside or outside the first one.
Book 2, on “The motion of bodies in resisting mediums”
Along with this there are a number of theorems and
conjectures about the properties of fluids.


Book 3, "The System of the World," is the
culmination: It makes use of the general results derived in
Book 1 to explain the motions of the planets and other
gravitational phenomena such as the tides. It begins with a
remarkable passage on "Rules of Reasoning in
Philosophy."
The four rules, reflecting the profound faith in the
uniformity of all nature, are intended to guide scientists in
making hypotheses, and in that function they are still up
to date. The first has been called a principle of
parsimony, and the second and third, principles of unity.
The fourth is a faith without which we could not use
the processes of logic.

Rule 1


Rule 2


No more causes of natural things should be admitted than are both true and
sufficient to explain their phenomena.
Therefore, the causes assigned to natural effects of the same kind must be, so
far as possible, the same.
Rule 3

Those qualities of bodies that cannot be intended and remitted [that is,
qualities that cannot be increased and diminished] and that belong to all
bodies on which experiments can be made should be taken as qualities of all bodies
universally.

Rule 4

In experimental philosophy. propositions gathered from phenomena by
induction should be considered exactly or very nearly true notwithstanding any
contrary hypotheses, until yet other phenomena make such propositions either
more exact or liable to exceptions.
9.4 Newton's First Law of Motion




We may phrase Newton's first law of motion, or law of inertia, as follows:
Every material body persists in its state of rest or of uniform,
unaccelerated motion in a straight line, if and only if it is not
acted upon by a net (that is, unbalanced external) force.
The essence is this: If you see a moving body deviating from a straight line,
or accelerating in any way, then you must assume that a net force (of
whatever kind) is acting on the body; here is the criterion for recognizing
qualitatively the presence of an unbalanced force.
There is implied only the definition of force as the "cause" of change of
velocity, a definition we already alluded to in our discussion of Galileo's
work. We recall that the Aristotelian scholastics had a rather different view
in this matter; they held that force was also the cause of uniform
(unaccelerated) motion.
It has been made plain that a net force must be supplied to change a body's
state from rest to motion or from motion to rest, from one speed to
another or from one direction of motion to another even at the same
speed.

Problem 9. 1 . Explain in terms of Newton's first law of
motion the common experience of lurching forward
when a moving train suddenly decelerates and stops.
Explain what happens to the passengers in a car that
makes a sharp and quick turn .
9.5 Newton's Second Law of Motion


In Newton's own formulation of the second law, he states
that the force acting on a body is equal to the
change of its quantity of motion, where "quantity
of motion" (later called "momentum ") is defined
as the product of mass and velocity.
It is customary to begin by stating the second law of
motion in the form: The net (external unbalanced)
force acting on a material body is directly
proportional to, and in the same direction as, its
acceleration.
or
9.5 Newton's Second Law of Motion


The constant so defined is a measure of the body's
inertia, for clearly a large ratio of Fnet to a means that a
large force is needed to produce a desired acceleration,
which is just what we expect to find true for large, bulky
objects
If we now symbolize the constant in Eq. (9.1 ), the
measure of inertia, by a letter of its own, m, and give it the
alternative name mass, we can write the second law of
motion:

In summary: Newton's second law, in conjunction with
the essentially arbitrary choice of one standard of mass,
conveniently fixes the unit of force, permits the
calibration of balances, and gives us an operational
determination of the mass of all other bodies.
9.6 Standard of Mass


It will readily be appreciated that the Standard of Mass that represents 1
kilogram, though essentially arbitrary, has been chosen with care. For
scientific work, 1/1000 of 1 kilogram, equal to 1 gram, was originally defined
as the mass of a quantity of 1 cubic centimeter (1 cm3) of distilled water at
4°C. This decision, dating from the late eighteenth century, is rather
inconvenient in practice. Although standardizing on the basis of a certain
amount of water has the important advantage that it permits cheap and
easy reproduction of the standard anywhere on earth, there are obvious
experimental difficulties owing to the effects of evaporation, the additional
inertia of the necessary containers, relatively poor accuracy for measuring
volumes, and so on.
Therefore, it became accepted custom to use as the standard of mass a
certain piece of precious metal, a cylinder of platinum alloy kept under
careful guard at the Bureau lnternationale des Poids et Mesures at Sevres, a
suburb of Paris (alongside what for a long time was defined as the standard
of length, a metal bar regarded as representing the distance of 1 meter) .
For use elsewhere, accurate replicas of this international standard of mass
have been deposited at the various bureaus of standards throughout the
world; and from these, in turn, auxiliary replicas are made for distribution
to manufacturers, laboratories, etc.


Fig. 9.3. Standard kilogram, a platinumiridium cylinder constructed in 1878,
held at Sevres, France, together with a
standard mete r.
Again, it was a matter of
convenience and accuracy
to make this metal block
have an inertia 1000 times
that of a I -g mass; and
thus the standard object
(see Fig. 9.3) is a cylinder
about 1 in. high of mass
1000 g, called 1 kg.
9.7 Weight











Objects can be acted on by all kinds of forces;
by a push from the hand;
by the pull on a string or spring balance attached to the object;
by a collision with another object;
by a magnetic attraction if the object is made of iron or other susceptible materials;
by the action of electric charges;
by the gravitational attraction that the earth exerts on bodies.
But no matter what the origin or cause of the force, and no matter where in the
universe it happens, its effect is always given by the same equation, Fnet = ma.
Newton's second law is so powerful precisely because it is so general, and because
we can apply it even though at this stage we may be completely at a loss to
understand exactly why and how a particular force (like magnetism or gravity)
should act on a body.
If the net force is, in fact, of magnetic origin, we might write Fmag = ma;
if electric, Fel = ma; and so forth.
Along the same line, we shall use the symbol Fgrav when the particular force involved
is the gravitational pull of the earth. Because this case is so frequently considered, a
special name for Fgrav namely weight, or a special symbol, W, is generally used.

Presupposed throughout the previous paragraphs was some
accurate method for measuring Fgrav .We might simply drop the
object, allowing Fgrav to pull on the object and to accelerate it
in free fall, and then find the magnitude of Fgrav by the relation.

Happily there is another method that is easier and more
direct. We need only our previously calibrated spring balance;
from it we hang the body for which Fgrav is to be determined,
and then wait until equilibrium is established. Now we do not
allow Fgrav downward to be the only force on the body but
instead we balance it out by the pull upward exerted by the
spring balance.

Fig. 9.4. Weighing with a
spring balance.
the pointer comes to rest-say on the
5-newton reading-then we know (by
Newton's first law) that the upward
pull of the spring, Fbal, just counter
balances the downward pull of Fgrav
on the object. The net force on the
body is zero. While oppositely
directed, these two forces on the
same object are numerically equal,
and therefore Fgrav' the weight in
question, must also be 5 newtons
(Fig. 9.4).

In summary, the dynamic
method of measuring weights
by Fgrav = m x g involves a
prior determination of mass
m and also a measurement of
g. Now, while g is constant for
all types of objects at a given
locality and may for most
purposes be taken as 9.80
m/sec2 or 32.2 ft/sec2 on the
surface of the earth, the exact
value is measurably different
at different localities.
Table 9. 1. Gravitational Acceleration
9.8 The Equal-Arm Balance



Before we leave the crucial-and initially perhaps troublesome-concept of mass, we must mention a third way of
measuring the mass of objects, in everyday practice by far
the most favored and accurate method.
By way of review, recall first that we need the essentially
arbitrary standard. Once this has been generally agreed on, we
can calibrate a spring balance by using it to give the standard
measurable accelerations on a smooth horizontal plane.
Then the calibrated balance can serve to determine other,
unknown masses, either :
(a) by a new observation of pull and resulting acceleration on the
horizontal plane, or
(b) by measuring on the balance Fgrav for the object in question and
dividing this value by the measured gravitational acceleration g at
that locality.



Fig. 9.5. Weighing with an equalarm balance.

To methods (a) and (b) we now add method (c),
known of course as "weighing" on an equal
arm balance-at first glance seemingly simple
and straightforward, but in fact conceptually most
deceptive.
We place the unknown mass mx on one pan (Fig.
9.5) and add a sufficient quantity of calibrated
and marked auxiliary-standard masses on the
other side to keep the beam horizontal.
When this point is reached, the gravitational pull
on the unknown mass, namely mx g, is
counterbalanced by the weight of the standards,
m,g. (Note that we assume here the sufficiently
verified experimental result concerning the
equality of gravitational accelerations for all
masses at one locality. )
But if mxg = msg, then mx = ms. Counting up the
value of all standard masses in one pan tells us
directly the value of the mass on the other side.
9.9 Inertial and Gravitational Mass


We see that case (a) on one hand and, (b) and (c) on the other measure two
entirely different attributes of matter, to which we may assign the terms inertial
mass and gravitational mass, respectively.
For practical purposes we shall make little distinction between the two types of
mass. But in order to remind ourselves how essential and rewarding it may be to
keep a clear notion of the operational significance of scientific concepts, and that,
historically, considerable consequences may follow from a reconsideration of longestablished facts in a new light, there are these words from Albert Einstein's and
Leopold Infeld's book The Evolution of Physics:


Is this identity of the two kinds of mass purely accidental, or does it have a deeper
significance? The answer, from the point of view of classical physics, is: the identity of the
two masses is accidental and no deeper significance should be attached to it. The answer of
modern physics is just the opposite: the identity of the two masses is fundamental and
forms a new and essential clue leading to a more profound understanding. This was, in fact,
one of the most important clues from which the so-called general theory of relativity was
developed.
A mystery story seems inferior if it explains strange events as accidents . It is certainly
more satisfying to have the story follow a rational pattern. In exactly the same way a
theory which offers an explanation for the identity of gravitational and inertial mass is
superior to the one which interprets their identity as accidental, provided, of course, that
the two theories are equally consistent with observed facts .
9.10 Examples and Applications of
Newton's Second Law of Motion


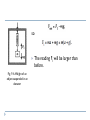
Examples 1. An object of mass m (measured in kg) hangs
from a calibrated spring balance in an elevator (Fig. 9 . 6 ) . The
whole assembly moves upward with a known acceleration a
(measured in m/sec2). What is the reading on the balance?
Solution: As long as the elevator is stationary, the upward pull
of the balance, and hence its reading FI, will be equal in
magnitude to the weight mg of the object. The same is true if
the elevator is moving up or down with constant speed, which
is also a condition of equilibrium and of cancellation of all
forces acting on m. However, in order to accelerate upward
with a m/sec2, m must be acted on by a net force of ma
newtons in that direction. In symbol form, Fnet = ma; but
so

Fig. 9. 6. Weight of an
object suspended in an
elevator
The reading FI will be larger than
before.


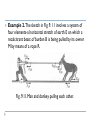
Fig. 9. 7. Atwood's
machine .

Examples 2. A string, thrown over a very light
and frictionless pulley, has attached at its ends the
two known masses m1 and m2, as shown in Fig.
9.7. Find the magnitude of the acceleration of the
masses.
Solution: In this arrangement, called Atwood's
machine, after the eighteenth-century British
physicist who originated it, the net external force
on the system of bodies is m2g = -m1g (again
assuming m2 to be larger than m1) The total mass
being accelerated is m1 + m2, and, consequently,
which we may solve with the known values of m1,
m2, and g for that locality.
9.11 Newton's Third Law of Motion


Newton's first law defined the force concept qualitatively, and the second law
quantified the concept while at the same time providing a meaning for the idea of
mass. To these, Newton added another highly original and important law of motion,
the third law, which completes the general characterization of the concept of
force by explaining, in essence, that each existing force on one body has its mirrorimage twin on another body.
In Newton's words,




To any action there is always an opposite and equal reaction; in other words, the actions of two
bodies upon each other are always equal and always opposite in direction: Whatever presses or
draws something else is pressed or drawn just as much by it.
If anyone presses a stone with a finger, the finger is also pressed by the stone.
If a horse draws a stone tied to a rope, the horse will (so to speak) also be drawn back
equally towards the stone, for the rope, stretched out at both ends, will urge the horse
toward the stone and the stone toward the horse by one and the same endeavor to go
slack and will impede the forward motion of the one as much as it promotes the forward
motion of the other.
 (Principia)
To emphasize all these points, we might rephrase the third law of motion as follows:
Whenever two bodies A and B interact so that body A experiences a force
(whether by contact, by gravity, by magnetic interaction, or whatever), then
body B experiences simultaneously an equally large and oppositely directed
force.
9.12 Examples and Applications of
Newton's Third Law




Example 1. The simplest case concerns a box (body A)
standing on the earth (body B). Let us identify the forces that
act on each. Probably the one that comes to mind first is the
weight of the box, Fgrav' We name it here F1A and enter it as a
vertically downward arrow, "anchored" to the box A at its
center of gravity (see Fig. 9.10a).
The reaction that must exist simultaneously with this pull of
the earth on the box is the pull of the box on the earth,
equally large (by the third law) and entered as a vertical,
upward arrow, F1B at the center of the earth in Fig. 9.10b. This
completely fulfills the third law. However, as the second law
informs us, if this were the complete scheme of force, the box
should fall down while the earth accelerates up.
This is indeed what can and does happen while the box drops
to the earth, settles in the sand, or compresses the stones
beneath it. In short, the two bodies do move toward each
other until enough mutual elastic forces are built up to
balance the previous set.
Specifically, the earth provides an upward push on the box at
the surface of contact, as shown in Fig. 9.10c by F2A an
upward arrow "attached" to the box, while, by the law now
under discussion, there exists also an equal, oppositely
directed force on the ground, indicated by F2B in Fig. 9.10d.
Fig. 9. 10. Forces on
box and earth in
contact.




There are now two forces on each body.
Equilibrium is achieved by the equality in magnitude of F1A and F2A
on A, and by F1B and F2B on B. But beware! F1A and F2A are not to be
interpreted as action and reaction, nor are F1B and F2B.
The reaction to F1A is F1B, and the reaction to F2A is F2B.
Furthermore, F1 and F2 are by nature entirely different sets of
forcesthe one gravitational and the other elastic.
In short, F1A and F1B are equally large by Newton's third law, but F1A
is as large as F2A (and F1B as large as F2B) by the condition of
equilibrium, derived from the second law.

Example 2. The sketch in Fig. 9. 11 involves a system of
four elements-a horizontal stretch of earth E on which a
recalcitrant beast of burden B is being pulled by its owner
M by means of a rope R.
Fig. 9.11.Man and donkey pulling each other.







Follow these four force couples: F1E is the push experienced by the earth,
communicated to it by the man's heels (essentially by static friction).
The reaction to F1E is the equally large force F1M exerted on the man by the earth.
The man pulls on the rope to the left with a force F2R and the reaction to this is the
force F2M with which the rope pulls on the man to the right.
A third set is F3B and F3R acting respectively on the donkey and on the rope. Finally,
the interaction between earth and animal is F4E and F4U.
In equilibrium, the separate forces on each of the four objects balance; but if
equilibrium does not exist, if the man succeeds in increasing the donkey's speed to
the left, then F3B - F4B = mbeast x a, and similarly for the other members of the
system.
And whether there is equilibrium or not, any "action" force is equal and opposite to
its " reaction."
The whole point may be phrased this way:



By the third law, the forces FIE and F1M are equal; similarly, F2M and F2R are equal.
But the third law says nothing whatever about the relationship of F1M to F2M two forces
arranged to act on the same body by virtue of the man's decision to pull on a rope, not by
any necessity or law of physics.
If there happens to be equilibrium, then FIM will be as large as F2M by Newton's second law
(or, if you prefer, by definition of "equilibrium " ) .
CHAPTER 10 : Rotational Motion




In the previous chapters we first acquainted ourselves with the description
of uniformly accelerated motions along a straight line, and in particular with
that historically so important case of free fall. Next came general projectile
motion, an example of motion in a plane considered as the superposition of
two simple motions. Then we turned to a consideration of the forces
needed to accelerate bodies along a straight line.
But there exists in nature another type of behavior, not amenable to
discussion in the terms that we have used so far, and that is rotational
motion, the motion of an object in a plane and around a center, acted on by
a force that continually changes its direction of action.
This topic subsumes the movement of planets, flywheels, and elementary
particles in cyclotrons. We shall follow the same pattern as before:
concentrating on a simple case of this type, namely, circular motion.
We shall first discuss the kinematics of rotation without regard to the
forces involved, and finally study the dynamics of rotation and its close ally,
vibration.
10.1 Kinematics of Uniform Circular Motion

Consider :




a point whirling with constant speed in a circular path about a center O;
the point may be a spot on a record turntable, or
a place on our rotating globe, or,
to a good approximation, the planet Venus in its path round the sun.
Before we can investigate this motion, we must be able to describe
it. How shall we do so with economy and precision? Some simple
new concepts are needed:
a) The frequency of rotation is the number of revolutions made
per second (letter symbol n), expressed in I/sec (or sec-t). A wheel
that revolves 10 times per second therefore has a frequency of n =
10 sec-1 While useful and necessary, the phrase "number of
revolutions" does not belong among such fundamental physical
quantities as mass, length, and time.

b) Next, we define the concept period of rotation (symbol T) as the
number of seconds needed per complete revolution, exactly the reciprocal
of n, and expressed in units of seconds.
The wheel would consequently have a period of rotation of 0.1 sec.
c) An angular measure is required. The angle a swept through by a point
going from P1 to P2 (Fig. 10.1) can, of course, be measured in degrees, but it
is more convenient in many problems to express  by the defining equation
Fig. 10. 1. Definition of an angle
in radian measure:  = s/r.
where s is the length of the arc and r is
the radius of the circle. This ratio of arc to
radius is a dimensionless quantity;
however, the name radians (abbreviation:
rad) is nevertheless attached to this
measure of angle, partly to distinguish it
from degrees of arc.
d) We now inquire into the velocity of a
particle executing uniform circular
motion. The word "uniform" means, of
course, that the rate of spin (the speed
s/t) does not change. Nevertheless, for
future reference, it is well to remember
that the velocity vector associated with
the rotating point does change in
direction from one instant to the next,
although its magnitude, represented by
the length of the arrows in Fig. 10.2, is
here constant.
Fig. 10.2

Let us now concentrate entirely on the
magnitude of the velocity, the speed,
given again by the ratio of distance
covered to time taken; if we know the
period or frequency of the motion and
the distance r from the spot to the
center of the circle, v is directly found
(usually in cm/sec) by realizing that s =
2r if t = T, that is,
e) The quantity  defined in this last
equation refers to the magnitude of the
tangential or linear velocity, i.e., to the
velocity of the point along the direction
of its path. Analogous to this time rate of
change of distance stands the powerful
concept angular velocity [symbolized
by the Greek letter  (omega)], which
is the time rate of change of angle. By
definition, for the type of motion we are
here considering,

If we happen to know n or T, we can find the magnitude
of the angular velocity from the fact that  = 2 if t = T,
or

The formal relation between  and v is evident if we
compare Eqs. (10.3) and (10.5):
10.2 Centripetal Acceleration


In the previous section that motion with constant speed
around a circle implies that the velocity vector is
continually changing in direction though not in magnitude.
According to Newton's laws of motion, a force must be
acting on a body whose velocity vector is changing in any
way, since if there were no net force it would continue to
move at constant velocity in a straight line.
And if there is a force, there must be an acceleration. So
when in circular motion with constant speed, a body is in
the seemingly paradoxical situation of being accelerated
but never going any faster (or slower)!


In the case of circular motion, the change in direction of the velocity
vector was shown in Fig. 10.2; we now need to analyze this change
in a little more detail (Fig. 10.3).
The vector labeled "v at P2" is the resultant of two other vectors,
which must be added together: the vector "v at PI" and the vector
"v" which represents the change in velocity that occurs during the
time interval t as the body moves along the circle from PI to P2
Fig. 10.3. How the velocity vector changes in circular motion at constant speed.

As can be seen from the· diagram, the vector v is directed
toward the center of the circle. The acceleration is defined as
the change in velocity divided by the time interval, in the limit
as the time interval becomes very small. In symbols:

Acceleration is also a vector, directed toward the center of the
circle; hence it is called the centripetal acceleration
("centripetal" means "seeking the center”) .
The corresponding force that must be acting on the body with
mass m to produce the acceleration is a vector in the same
direction, F= ma according to Newton's second law; in this
case, F is called the centripetal force.



Unfortunately the ordinary language that we use to describe
motion causes confusion at this point. We are accustomed to
hearing talk about "centrifugal" force, a force that is said to
act on a whirling body in a direction away from the center.
We shall not use this term, because there is no such force,
despite the illusion. If you tie a weight on a string and twirl it
around your head (Fig. 1 0.4)
Fig. 10.4. A centripetal force acts on the stone, while a centrifugal force acts on the
string and hand .



You think you can feel such a force, but that is a force acting on you at the
center, not a force acting on the whirling body; it is in fact the third-law
reaction to the centripetal force acting on the whirling weight. Or, if the
string breaks, you see the object flying away along the tangent of the
circular path it was following just before the break. But no force pulls it in
flight (not counting gravity, downward) and it does not move off along a
radius either.
Isaac Newton was one of the first to recognize that all these phenomena
are due to the natural tendency-inertia-of any body to keep on
moving in the same direction if it is not constrained to do otherwise.
If the string breaks when the weight is at the point P1 (Fig. 10.3), it will "fly
off on a tangent" (not along the radius)that is, it will continue to move in
the direction indicated by the arrow of the velocity vector at P1. While the
object is still attached to the string and moving in a circle, you have to
provide a force on it toward yourself-the centripetal force--to prevent it
from flying off. And since you are exerting a force on the string, the string
must also, by Newton's third law, exert an equal and opposite force on your
hand. The outward force that you feel is the reaction to the force you apply.

The result for the magnitude of the centripetal acceleration is
very simple:

Let us summarize its physical meaning by quoting Newton in
the Principia of 1687, a very clear discussion and one that
indicates how Newton was able to make connections between
a great variety of situations:




Centripetal force is the force by which bodies are drawn from all
sides, or are impelled, or in any way tend, toward a point as to a
center.
One force of this kind is gravity, by which bodies tend toward
the center of the earth;
another is magnetic force, by which iron seeks a lodestone;
and yet another is that force, whatever it may be, by which the
planets are continually drawn aside from rectilinear motions
and compelled to revolve in curved lines orbits.
10.3 Derivation of the Formula for Centripetal
Acceleration and Centripetal Force





In Fig. 10.3, a point moves uniformly through an angle  from P1 to P2 along
the arc s.
The speeds at Pl and P2 are equal, but the direction of the velocity vectors
changes through angle  between Pl and P2.
The change of velocity, v is obtained graphically in the usual manner in Fig.
10.3b.
Now note that the triangle there, and the one contained by P1OP2 in Fig.
10.3a, are similar isosceles triangles. Therefore v/v = x/r and v = vx/r.
On dividing both sides by At, the time interval needed for this motion, we
obtain v/t = vx/r At. The left side represents the average acceleration a
during t; and if, as in Chapter 6, we restrict t to smaller and smaller
values, in the limit as t approaches 0, the average acceleration becomes
equal to the instantaneous acceleration a:

At the same time, however, as t ( and with it, )
decreases, the line x becomes more and more nearly
equal to the arc s, so that in the limit, x = s, and we write

We note finally that as t  0, s/t  v, the
instantaneous velocity of the moving point, so that the
formula for centripetal acceleration becomes

Earlier we found v = r; thus a is also expressed by





The physical causes and means for providing a rotating object
with the necessary centripetal force vary greatly.
A rotating flywheel is held together by the strength of the
material itself, which can supply the stress, at least up to a
point.
A car rounding a curve on a level road is kept from flying
off tangentially in a straight line by the force of friction, which
supplies the centripetal force by acting ( sideways ) on the
tires.
The moon, as Newton first explained, is kept captive in its
orbit about the earth by the gravitational pull continually
experienced by it.
The electron circulating around an atomic nucleus in
Niels Bohr's model (Chapter 28) does so by virtue of electric
attraction to the center.