Download Chapter 8 Multielectron Atoms – Spin and Term Symbols

Chapter 8
Multielectron Atoms – Spin
and Term Symbols
8.1
Electron Spin
Electron spin is a form of angular momentum different from orbital angular
momentum. It represents the “top-like” spinning behavior of electrons.
The spin quantum number ms was introduced to account for the experimental
observation of a doublet in the atomic spectrum of sodium. The Schrödinger
equation (without spin) predicted only a single line.
Recall the eigenequations for orbital angular momentum:
L̂2 Ylm (θ, φ) = h̄2 l(l + 1)Ylm (θ, φ)
L̂z Ylm (θ, φ) = mh̄Ylm (θ, φ)
1
l = 0, 1, 2, ...
−l ≤m≤l
Similarly, we can write eigenequations for spin angular momentum:
α
α
2
Ŝ
= h̄ s (s + 1)
β
β
| {z }
2
s=
1
2
α or β
Ŝz
α
β
= ms h̄
α
β
− s ≤ ms ≤ s
ms = ±
1
2
Note: For α, ms = 21 ; and for β, ms = − 12 .
The eigenfunctions α(σ) and β(σ) are never given a real form, but can be
1/2
−1/2
formally associated with α = Y1/2 and β = Y1/2 (i.e. use formal association
for orthogonality relations and relation with spin operators...)
We now have a fourth quantum number ms , the spin quantum number, and
two spin functions α(σ) and β(σ) (where σ is a “spin variable”). This gives
us one more degree of freedom – that of spin.
Note that α and β are eigenfunctions of both Ŝ 2 and Ŝz , which are Hermitian
operators, and therefore they are orthogonal:
Z
∗
α (σ)β(σ)dσ =
Z
β ∗ (σ)α(σ)dσ = 0
We assume they are also normalized:
Z
∗
α (σ)α(σ)dσ =
Z
β ∗ (σ)β(σ)dσ = 1
Spin angular momentum has no classical analog, so do not try to attach a
“classical” meaning to it.
2
8.2
Pauli Exclusion Principle
Now that we have introduced spin, a many (N ) electron wave function can
be written:
Ψ(~r1 σ1 , ~r2 σ2 , ...~rN σN ) = Ψ(1, 2, ...N )
Here, ~r1 = (x1 , y1 , z1 ) represents the spatial varibles of electron 1,
and σ1 is the spin variable of electron 1.
So when one writes
Z
...
Z
R
Ψ∗ (1, 2, ...N )Ψ(1, 2, ...N )dτ , it means:
Ψ∗ (1, 2, ...N )Ψ(1, 2, ...N )dx1 dy1 dz1 dσ1 , ...dxN dyN dzN dσN
R
Note: This is a 4N-dimensional integral! (Remember (f unction) dτ means
integration over the entire space of all the varibles.)
The Pauli Principle states that all electronic wavefunctions must be antisymmetric under the interchange of any two electrons.
e.g. Ψ(1, 2) = −Ψ(2, 1)
This is an implication of two facts:
1. Electrons are indistinguishable:
|Ψ(1, 2)|2 = |Ψ(2, 1)|2
2. Two electrons with the same spin can’t be on top of one another:
|Ψ(1, 1)| = 0
3
8.3
Term Symbols
Term symbols are used to describe atomic spectra and predict the ground
state electron configuration.
Knowing only the number of electrons does not give us a detailed enough
description.
e.g. Carbon: 1s2 2s2 2p2 leaves us with unanswered questions:
which p orbitals have electrons?
what is the spin state?
Using atomic term symbols gives us a detailed specification of the electron
configuration. Term symbols have the form:
2S+1
LJ
L: total orbital angular momentum
S: total spin angular momentum
2S + 1: spin multiplicity
J: total angular momentum (Russel-Saunders coupling of L and S)
where
J = L + S, . . . , |L − S|
0 1 2 3 ···
L =
S P D F ···
X
ML =
m`i = Lz
i
Ms =
X
msi = Sz
i
Note: For a filled shell (i.e. ns2 , np6 , nd10 , ...) the term symbol is always:
1
S0
4
8.3.1
An Example
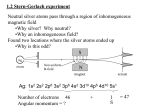
What are the possible term symbols for an np3 electron configuration?
We don’t have to worry about fully occupied subshells, because their
contribution to ML and MS is always zero. (See pg. 295 for the explanation.)
Thus we have enough information to solve this problem, only knowing the
unfilled subshell.
L = 2, 1, 0 since ML can be -2, -1, 0, 1, or 2.
For L = 2 S = 12 since there is one unpaired electron (the one in the
ml = 0 orbital). Thus J = 52 , 32 . So we have 2 D 5 and 2 D 3 .
2
2
For L = 1 S = 21 since there is one unpaired electron (the one in the
ml = −1or1 orbital). Thus J = 32 , 12 . So we also have 2 P 3 and 2 P 1 .
2
2
Finally, for L = 0 S = 23 since all three electrons are unpaired (there is
one in each of the ml orbitals (-1, 0, and 1)). Thus J = 32 . So there is one
more term symbol, 4 S 3 .
2
8.4
Finding the Number of Microstates
The number of microstates is given by:
G!
N !(G − N )!
where G is the number of spin orbitals and N is the number of electrons.
Note: If N = G, the number of states is 1.
The number of states per term symbol can also be found:
(2L + 1)(2S + 1)
5
8.5
Hund’s Rules
Hund’s Rules tell us how to determine the ground state of a configuration
based on its term symbols.
Hund’s Rules
1. The state with the larger value of S (higher multiplicity) is more stable.
2. For states with the same S, the one with the larger L is more stable.
3. For states with the same S and L:
• if subshell is less than half filled, the smaller J is more stable
• if subshell is more than half filled, the larger J is more stable
8.5.1
An Example
Apply Hund’s rules to the term symbols found in 8.3.1.
4
S 3 is the most stable, by # 1.
2
8.6
8.6.1
More Examples
Zr
Zr has a ground state configuration of [Kr]4d2 5s2 . What is its ground state term
symbol?
We only need to concern ourselves with the unfilled subshell (4d2 ). According to Hund’s Rules, we are looking for the highest multiplicity, thus as
many spins as possible should be parallel. In this case, all of the spins can be
parallel, giving S = 1. There are many states like this though, so we move
on to the next rule, which tells us to find the highest L. A state like:
↑↑
−2 −1 0 1 2
6
has the maximum value of L (under the constraint that the spins are all
parallel), which is 3. Since S = 1 and L = 3, J can be 4,3, or 2. By # 3, the
ground state has the lowest J, since this subshell is less than half full. Thus
the ground state term symbol for Zr is 3 F2 .
8.6.2
Fe
Fe has a ground state configuration of [Ar]3d6 4s2 . What is its ground state term
symbol?
There are six electrons we need to worry about, but only 5 orbitals, thus
there will be at least one spin pair, so the maximum S = 2. The maximum
L is from a state like:
↑ ↑ ↑ ↑ ↑↓
−2 −1 0 1 2
Since S = 2 and L = −2 + −1 + 0 + 1 + 2 + 2 = 2, J can be 4, 3, 2, 1,
or 0. Because this subshell is more than half filled, the ground state has the
highest J, which is 4. Therefore the ground state of Fe is 5 D4 .
8.7
Atomic Spectra
Term symbols allows us to predict atomic spectra by following a few simple
selection rules.
Selection Rules for Atomic Spectra
• ∆L = ±1
• ∆S = 0
• ∆J = 0, ±1
except
J =0→J =0
7
8.7.1
An Example
List all of the allowed transitions between the sodium states 2 S 1 , 2 P 3 , 2 P 1 , 2 D 3 ,
2
2
2
2
2
D 1 , 2F 7 , 2F 5 .
2
2
2
2
→
2
→
2
→
2
P3
→
2
D1
2
P1
→
2
D3
2
P1
→
2
D1
D3
→
2
F5
S1
2
2
S1
2
2
P3
2
2
2
2
2
2
2
P3
2
P1
2
D3
2
2
2
2
2
A few examples of transitions that are not allowed (and why) are:
2
S1
→
2
D3
→
2
2
2
2
D3
because
∆L = 2
F7
because
∆J = 2
2
2
8