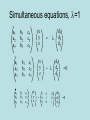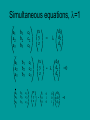Download Algebraic functions

Determinants
and Matrices
行列式與矩陣
Chapters 17 & 18
Gialih Lin, Ph. D. Professor
17.1 Concepts
• Linear algebra :matrix
• The concept of determinants has its origin
in the solution of simultaneous linear
equations. 聯立方程式
• a1x+b1y=c1
• a2x+b2y=c2
• x=(c1b1-b1c2)/(a1b2-b1a2)
• y=(a1c2-c1a2)/(a1b2-b1a2)
determinant
• The solution of the
system can be written
in the form
• x=D1/D
D=
D1=
• y=D2/D
D2=
a1
b1
a2
b2
c1
b1
c2
b2
a1
c1
a2
c2
17.2 Determinants of order 3
• a1x+b1y+c1z=d1
a2x+b2y+c2z=d2
a3x+b3y+c3z=d3
• x=D1/D
• y=D2/D
• z=D3/D
• Gramer’s rule
D 3=
a1
b1
d1
a2
b2
d2
a3
b3
d3
a1
D=
b1
c1
a2 b2
c2
b3
c3
a3
D1=
D2=
d1 b1
c1
d2 b2
c2
d3 b3
c3
a1 d1
c1
a2 d2
c2
a3 d3
c3
Simultaneous equations, l=1
a1
a2
a3
a1
a2
a3
a1
a2
a3
b1
b2
b3
b1
b2
b3
b1
b2
b3
x
y
z
c1
c2
c3
x
y
z
c1
c2
c3
c1
c2
c3
x
y
z
-
l
=
-
1
0
0
0
1
0
l
0
0
1
d1
d2
d3
d1
d2
d3
d1
d2
d3
=0
=0
Hermitian transformation
• Change the length of vector r but not its direction
• Hr = h r
r
s
• h is a real number
H11 H12 H13
H21 H22 H23
H31 H32 H33
a1
a2
a3
=
h
a1
a2
a3
17.3 The general case
Wave functions
 y1 = a11f1+a12f2+a13f3+ ….+a1nfn
 y2 = a21f1+a22f2+a23f3+ ….+a2nfn
• ..
…..
 yn = an1f1+an2f2+an3f3+ ….+annfn
Quantum mechanics
• Any function, y, can be
expressed in terms of its
components for a set of
basis functions, fi, of
unit length (column
matrices or column
vectors, see Chapter 18)
 y=
a1f1+a2f2+a3f3+ ….+anfn
 F=
b1f1+b2f2+b3f3+ ….+bnfn
a1
a2
.
.
.
an
17.4 The solution of linear
equations
• Gramer’s rule
• D=0
• no solution exists because the equations
are inconsistent. The equations are said
to be linearly dependent, and each
equation can be expressed as a linear
combination of the others.
Secular equations
•
•
•
•
Shrödinger equation
Hy = Ey
In the form of matrix
H is an nxn matrix for an n order wave
function (y)
• E is a constant called as eigenvalue (See
chapter 18)
Hermitian transformation and eigenvalue
(see Chapter 19)
• Change the norm of function y, but keep the relative magnititudes of its
components along its basis functions the same. (see Section 18.5 linear
transformation)
• Hy = h F
• h is a real number, and y is said to be an eigenfunction of operator H. (see
chapter 19 The matrix eigenvalue problem) The operator H is said to be
Hermitian when (as in quantum mechanics) the eigenvalue h is real.
H11 H12 ... H1 n
H21 H22 ... H2n
.
.
.
Hn1 Hn2 ... Hnn
a1
a2
.
.
.
an
= h
a1
a2
.
.
.
an
Secular determinant
• The eigenvalue, h, of the Hermitian operator, H, are
calculated by solving the secular determinant
(H11 -h) H12
...
H21 (H22-h) ...
.
.
.
Hn1 Hn2 ...
H 1n
H 2n
(Hnn-h)
=0
18 Matrices and linear
transformations
•
•
•
•
•
•
18.1 concepts
3x3 (square) matrix
Row
Column
Trace
Tr A = a1+b2+c3
A=
a1
a2
a3
b1
b2
b3
c1
c2
c3
Vectors
• A matrix containing a single column only is
called a column matrix or column vector; a
matrix containing one row only is a row
matrix or row vector. The elements of a
vector are called components.
Quantum mechanics
• Any function, y, can be
expressed in terms of its
components for a set of
basis functions, fi, of
unit length (column
matrices or column
vectors, see Chapter 18)
 y=
a1f1+a2f2+a3f3+ ….+anfn
 F=
b1f1+b2f2+b3f3+ ….+bnfn
a1
a2
.
.
.
an
Matrix multiplication
• C=AB
• The number of columns of A=the number
of rows of B. if A is mxn and B is nxp, the
procdut C is mxp
Hermitian transformation
• Change the length of vector r but not its direction
• Hr = h r
r
s
• h is a real number
H11 H12 H13
H21 H22 H23
H31 H32 H33
a1
a2
a3
=
h
a1
a2
a3
Multiplication by a unit matrix
• If A is an mxn matrix and Im and In are the
unit matrices of orders m and n,
respectively, then
• Im A= A =A In
Simultaneous equations, l=1
a1
a2
a3
a1
a2
a3
a1
a2
a3
b1
b2
b3
b1
b2
b3
b1
b2
b3
x
y
z
c1
c2
c3
x
y
z
c1
c2
c3
c1
c2
c3
x
y
z
-
l
=
-
1
0
0
0
1
0
l
0
0
1
d1
d2
d3
d1
d2
d3
d1
d2
d3
=0
=0
18.5 Linear transformations
•
•
•
•
x’ = Ax
Simultaneous transformations
Consecutive transformations
Inverse transformations
Hermitian transformation
• Change the length of vector r but not its direction
• Hr = h r
r
s
• h is a real number
H11 H12 H13
H21 H22 H23
H31 H32 H33
a1
a2
a3
=
h
a1
a2
a3