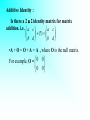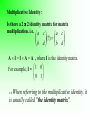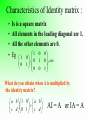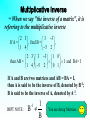Download Sec 3 Add Maths : Matrices

Introduction
• Matrices have many important uses.
• One of the simplest uses of matrices is to
store data.
• In fact, this is the most common use outside
mathematics.
• Matrices are used to solve linear systems
and represent geometric figures and
transformations. Building on this geometric
interpretation, matrices can also be applied
in the study of trigonometry.
•Matrices are a powerful unifying concept,
connecting ideas in mathematics to those in other
content domains as well as connecting various
branches of mathematics. As such, matrices can be
a means of integrated whole rather than a set of
isolated topics.
•Matrices are a rich topic and that many uses of
matrices are minor extensions or applications of
content already in our syllabus. There are several
reasons for introducing matrices into the syllabus:
1
• Matrices introduce a fundamental concept
in discrete mathematics.
• They model numerous realistic applications.
• They furnish opportunities for doing
arithmetic and algebraic computation in a
new context.
• Their properties and their operations lead to
important theoretical results.
Why Learn Matrices
•
•
•
•
•
•
Storing and organising numerical data
Operations with matrices
The identity Matrices
Inverse Matrices
Operations using a Spreadsheet
Some interesting Applications of Matrices (
not in syllabus)
Storing and organising numerical data
Passes At
Year
PSLE
1
GCE O Level
Annual Output
2
GCE A Level
3
ITE
4
Per Cent
Polytechnic
5
University
6
Number
1995
94.2
90.9
86.3
7325
11008
7926
1996
95.5
90.8
85.4
5581
12105
8218
1997
95.7
90.3
84.2
4918
12919
8679
1998
95.0
91.1
86.0
6234
13904
9331
1999
96.2
92.1
86.5
8501
14641
9463
2000
95.8
92.3
85.4
8427
15074
9406
6 rows and 7 columns of data,
we say the matrix has size (order) 6  7
Example :
Type
Friction Textbooks General Reference
Malay
25
47
22
30
Chinese
40
72
38
40
English
80
85
67
54
Malay
Chinese
Type
English
Friction
25
40
80
Textbook
47
72
85
General
22
38
67
Reference
30
40
54
 25 47 22 30 


40
72
38
40


 80 85 67 54 


3  4 Matrix
 25

 47
 22

 30
40 80 

72 85 
38 67 

40 54 
43
Matrix
Text Book Page 198
• Can you name the orders of the following
matrices?
(a) 2 by 2
(e) 3 by 5
(b) 3 by 1
(f) 2 by 1
(c) 1 by 4
(g) 1 by 1
(d) 3 by 3
Operations with Matrices
• Addition and Subtraction of Matrices
 25 47 22 30   5 2 3 7   30 49 25 37 

 
 

40
72
38
40

12
11
7
10

52
83
45
50

 
 

 80 85 67 54   20 15 14 18  100 100 81 72 

 
 

 30 49 25 37   7 4 6 5   23 45 19 32 

 
 

52
83
45
50

18
7
2
7

34
76
43
43

 
 

100 100 81 72  15 25 10 8   85 75 71 64 

 
 

What do you notice about the order of the two
matrices involved in each case?
Rules for Matrix Addition
and Matrix Subtraction
• If P and Q are two matrixes of the same order,
then the sum of P and Q, denoted by ( P + Q ), is a
matrix with its elements being the sum of the
corresponding elements of P and Q.
• The difference of P and Q is denoted by
(P–Q).
• If P and Q are of different orders, then their sum
and difference are not defined.
Example :  1   3 8 
 

3
5

2
  

Ex 9A Page 201
• Class Work :
• Q1 a to j
Multiplication of a Matrix by a Real Number
• Examples :
 4 3
A

 2 10 
B  2A
 4 3
B  2

 2 10 
8 6
B

 4 20 
1 6
C 

 3 5 
2
D C
3
2 1 6 
B 

3  3 5 
 2

4 
 3
B

 2  10 


3

Some Special Matrices
• Square Matrix
* A matrix has the same number of rows and
columns.
1 3 2
 2 7 


Examples : 
2
by
2
0
1
2


 3 by 3
3
8
1 3 0


•Zero matrix or null matrix , denoted by O
* Every element of a matrix is zero.
* May be of any order
Examples :
0 0

 ,
0 0
 0
,
0
 0
 
,
0 ,
 

 0
0
 
0
0 0  ,....
Ex 9A Page 201
•
•
•
•
•
Class work :
Q3
Q4a, c, e, f
Q5a, c, e
Q6a
•
•
•
•
•
Homework :
Q2
Q4b, d
Q5b, d
Q6b
Operations With Matrices
Matrix multiplication was invented in the 19th
Century as a useful way of combining two
suitable matrices. It multiplies elements in a row
with elements in a column to produce one single
number.
To make up some matrix multiplication problems
for yourself. And to investigate the condition on
the sizes of two matrices that is necessary before
you can be multiplied.
Example : Maybeline bought 3 apples, 2 oranges and 4
pears.The cost of each item is 25 cents, $1 and 40 cents
respectively. Find the total cost of the purchase.
Answer : The total cost of the purchase
= 3  25 cents + 2  100 cents + 4  40 cents
= 435 cents
= $ 4.35
 25 
Using Matrices :


 3 2 4  100 
 40 


  3  25  2 100  4  40 
  435 
• Page 202, 203
• For example,
• A 33 matrix multiplied by a 32 matrix
will result in a 32 matrix.
• A 32 matrix multiplied by a 23 matrix
will result in a 33 matrix.
• A 32 matrix multiplied by a 33 matrix is
not possible.
• In general : A m  n matrix can be
multiplied to a n  p matrix to produce a
m  p matrix.
Ex 9B Page 206
•
•
•
•
•
•
•
•
•
•
•
Class Work :
Q1b, d, f
Q2
Q3a
Q4
Q6a, c, f
Q8
Q10
Q11
Q12
Q14
•
•
•
•
•
•
•
Homework :
Q1a, c, e
Q3b, c
Q5
Q6b, d, e
Q9
Q13
Matrices Multiplication
 95 115 36 


V   78 36 98 
 65 72 75 


The prices of the drinks
per cup are 55¢ for tea,
60¢ for coffee and 75¢ for
drinking chocolate.
(a) Form a matrix of prices and use it to find
the total amount taken on each of the 3 days.
(b) What information would be found by premultiplying V by (1 1 1)?
explain why the matrix of prices can be a 31 or 13
matrix in (a) and what information is found if V is
post-multiplied by  1 
1
1
 
Commutative and associative properties
matrix multiplication is not
commutative but associative.
Explain using a
problem
I II
Hill 10 5
Plain  5 10
Dale  6 4
III IV
1 2
2 5
5 3 
Doors
I
2
2
II
3
III
3
IV

Windows
12 
20 
15 
20 
Commutative and associative properties
I II
Hill 10 5
Plain  5 10
Dale  6 4
A
III IV
1 2
2 5
5 3 
Doors
I
2
2
II
3
III
3
IV

B
Windows
12 
20 
15 
20 
Prices
100 
 80 


C
(AB)C is calculated by first finding the number of
What
matrix AB
doors
and information
windows in eachdoes
of thethe
developments
and
then
findingBA
the
gives?
? total cost of windows and doors for
each development.
A(BC)Calculate
is calculated(AB)C
by firstand
finding
the cost of the
A(BC).
doors and windows in each model and then finding
they
are equal.
their Explain
total costwhy
for each
development.
Commutative and associative properties
• In general, matrix multiplication is not
commutative, i.e. AB  BA. ( Ex 9B Q 2 )
• However, matrix multiplication is
associative. (AB)C = A(BC) ( Eg of
previous 2 slides)
• See example 4 on page 205
Identity Matrices
• In the addition of numbers, the identity is 0
since x + 0 = x for every value of x.
• In the multiplication of numbers, the identity is 1
since x  1 = x for every value of x.
If you combine the matrix I with any matrix P and
the result is the matrix P, then I is known as the
identity matrix.
Additive Identity :
Is there a 2  2 identity matrix for matrix
addition. i.e.  a c 
a c 

  (?)  

b d 
b d 
•A + O = O + A = A , where O is the null matrix.
For example, O =  0 0 


0 0
Multiplicative Identity :
Is there a 2  2 identity matrix for matrix
multiplication. i.e.  a c 
a c 

(?)  

b d 
b d 
A  I = I  A = A , where I is the identity matrix.
For example, I =  1 0 


0 1
When referring to the multiplicative identity, it
is usually called "the identity matrix".
N.B.
Characteristics of Identity matrix :
•
•
•
•
Is is a square matrix
All elements in the leading diagonal are 1.
All the other elements are 0.
Eg  1 0   1 0 0 

0
,0
1 
0
1
0
0  , etc
1 
What do you obtain when A is multiplied by
the identity matrix?
 a b  1 0   a b 




c
d
0
1
c
d


 

AI = A or IA = A
Inverse Matrices
• The inverse of anything is that which will
combine with it to give the identity.
a
Is there an additive inverse for 
b
a
The additive inverse of 
b

Reason :
c
?
d
c

is

d
 a c    a c   0
 b d    b  d    0

 
 
  a c 
 b  d 


0

0
The additive inverse can be found easily.
Multiplicative Inverse
** When
we say "the inverse of a matrix", it is
referring to the multiplicative inverse
 2 3
 3 3 
If A = 
 , find B = 
,
1 4
 5 2 
 2 3   3 3   1 0 
then AB = 


  I and BA= I
 1 4   5 2   0 1 
If A and B are two matrices and AB = BA = I,
then A is said to be the inverse of B, denoted by B-1;
B is said to be the inverse of A, denoted by A-1.
IMPT NOTE :
1
B 
B
-1
You are doing Matrices .
Given A and the inverse of A, denoted by A-1
IMPT NOTE :
1
A 
A
-1
You are doing Matrices .
AA  I
-1
A A  I
-1
To find the inverse of a matrix A =
a b

.
c d 
Step 1 : Find the determinant of the matrix A,
denoted by det A
det A =
Note :
a b
c d
 ad  bc
• If det A = 0, then the inverse of A is not defined.
•Hence A does not have an inverse.
•When a matrix does not possess an inverse, it is known as a
singular matrix.
Step 2 : The inverse of matrix A is
1  d b 


ad  bc  c a 
Ex 9C Page 211
•Class Work:
•Homework:
•Q1a, b, h
•Q1e,i
•Q2a, d,e
•Q2g,h
•Q4
•Q3
•Q5
•Q7
•Q6
•Q8
•Q9
•Q10
Time to think
• Can a matrix have more than one inverse?
How to prove it?
• Text Book Page 214
• 9.9 Some interesting Properties of
Matrices
• Q1, 2
Using Matrices to Solve
Simultaneous Equations
• To solve simultaneous equations by using
simple algebra, if there is no solution or
infinite solutions, what will you say about
the two equations?
• The simultaneous equations will represent
either two parallel lines or the same straight
line.
Using Matrices to Solve
Simultaneous Equations
• When the simultaneous equations is
expressed in the matrix form, and if the
determinant of the 22 matrix is zero, then
the two simultaneous equations will
represent either two parallel lines or the
same straight line.
• The equations have no unique solution.
Using Matrices to Solve
Simultaneous Equations
•Step 1 : Given ax + by = h
and
cx + dy = k

 a b  x   h 

    
 c d  y   k 
a b
•Step 2 : Find determinant of 

c d

a b
•Step 3 : If
0 ,
 x
1  d b  h 
then   

 
y

c
a
ad

bc
 

 k 
c d
•Step 3 : If
a
b
c
d
 0 , the equations have no unique solution.
Ex 9D Page 214
•
•
•
•
•
•
Class work:
Q1, 3, 5,8
Q10
Q12
Q13
Q14
•
•
•
•
Homework:
Q2, 4, 6
Q9
Q11
Why learn Matrices ?
The interior design company is given the job of putting up
the curtains for the windows, sliding doors and the living
room of the entire new apartment block of the NTUC
executive condominium. There are a total of 156 threebedroom units and each unit has 5 windows, 3 sliding
doors and 2 living rooms. Each window requires 6 m of
fabric, each sliding door requires 14 m of fabric and each
living room requires 22 m of fabric. Given that each metre
of the fabric for the window cost $12.30, the fabric for the
sliding door costs $14.50 per metre and each metre of the
fabric for the living room is $16.50.
We can write down three matrices whose product shows
the total amount of needed to put up the curtains for each
unit of the executive condominium.
NE Message:
The property market in Singapore went up very rapidly in
the 1990’s. Many Singaporeans dream of owning a private
property were dashed and many call for some form of help
from the government to realise their dream. NTUC Choice
Home was set up to go into property business as a way of
stabilising the market and to help Singaporeans achieve
their dream of owning private properties. With the onset of
the Asian economic crises, the property market went under
and the public start to question the need for NTUC Choice
Home and urged NTUC to dissolve NTUC Choice Homes.
Do you think this is a good request? How long do you
think it will take to set up a company to run the property
business?
Operations using a Spreadsheet
The Microsoft Excel matrix functions are:
• MDETERM(array)
Returns the matrix determinant
of an array
• MINVERSE(array)
Returns the inverse of the
matrix of an array
• MMULT(array A, array B) Returns the matrix
product
• TRANSPOSE(array) Returns the transpose of an
array. The first row of the input
becomes the first column of the
output array, etc.
• *Except for MDETERM(), these are array functions and
must be completed with "Crtl+shift+Enter".
Some Interesting Applications
• Routes matrices or Matrices for Graphs
Matrices can be used to store data about graphs. The graph
here is a geometric figure consisting of points (vertices)
and edges connecting some of these points. If the edges are
assigned a direction, the graph is called directed.
• Cryptography
Matrices are also used in cryptography, the art of writing or
deciphering secret codes.
Routes Matrices
Example If 5 places A, B, C, D, E are connected by a road
system shown in the graph. The arrows denote one-way roads,
then this can be listed as
To
From
A
B
C
D
E
A
0
1
1
1
0
B
1
2
0
0
1
C
2
0
0
1
1
the loop at B gives 2
routes from B to B
but the loop at D gives
only 1 route because
it is one-way only.
R=
D
0
0
1
1
1
0
1
1
1
0

B
E
1
1
2
1
0
1
2
0
0
1
A
2
0
0
1
1
0
0
1
1
1
1
1
2
1
0 
E
C
D
• Multiplying this matrix by itself gives R2 which
gives the number of possible two-stage routes
from place to place. E.g. the number in the 1st row,
1st column is 3 showing there are 3 two-stage
routes from A back to A (One is ABA, another is
ACA using the two-way road and the third is ACA
out along the one-way road and back along the
two-way road.)
• Similarly, R3 gives the number of possible threestage routes from place to place and vice versa.
A spreadsheet can be used for the tedious matrix
operations as shown below.
Cryptography
• One way of encoding is associating numbers with
the letters of the alphabet as show below. This
association is a one-to-one correspondence so that
no possible ambiguities can arise.
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z


























26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
In this code, the word PEACE looks like 11 22 26 24 22.
Suppose we want to encode the message: MATHS IS
FUN
If we decide to divide the message into pairs of
letters, the message becomes MA TH IS SF UN.
• (If there is a letter left over, we arbitrarily
assign Z to the last position). Using the
correspondence of letters to numbers given
above, and writing each pair of letters as a
column vector, we obtain
 M    14   T    7 
   
 A   26   H  19 
 S    8 
 I  18 
 S    8 
 F   21
U  6 
  
 N  13 
• Choose an arbitrary 2  2 matrix A which
has an inverse A-1. Say A =  2 3  and
1 2

A-1 =  21 23


Now transform the column vectors by multiplying each
of them on the left by A:
The encoded message is 106 66 71 45 70 44 79 50 51 32.
To decode, multiple by A-1 and reassigning letters to the
numbers.