* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download HARVARDx | HARPH525T114-G007300_TCPT
Quantitative trait locus wikipedia , lookup
Long non-coding RNA wikipedia , lookup
Polycomb Group Proteins and Cancer wikipedia , lookup
Oncogenomics wikipedia , lookup
Epigenetics of diabetes Type 2 wikipedia , lookup
Essential gene wikipedia , lookup
Gene nomenclature wikipedia , lookup
History of genetic engineering wikipedia , lookup
Metagenomics wikipedia , lookup
Therapeutic gene modulation wikipedia , lookup
Gene desert wikipedia , lookup
Site-specific recombinase technology wikipedia , lookup
Nutriepigenomics wikipedia , lookup
Pathogenomics wikipedia , lookup
Minimal genome wikipedia , lookup
Genomic imprinting wikipedia , lookup
Public health genomics wikipedia , lookup
Genome evolution wikipedia , lookup
Ridge (biology) wikipedia , lookup
Genome (book) wikipedia , lookup
Epigenetics of human development wikipedia , lookup
Microevolution wikipedia , lookup
Gene expression programming wikipedia , lookup
Artificial gene synthesis wikipedia , lookup
Biology and consumer behaviour wikipedia , lookup
Designer baby wikipedia , lookup
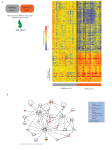
HARVARDx | HARPH525T114-G007300_TCPT In this module we're going to be explaining the mathematics and statistical methods that we need to be able to make a heat map, which is a figure that appears in many, many genomics publications and in many analyses. In this figure we see that there are these dendrograms up on top and on the side. We're going to learn what those are and how to make them. And then we also see these colors. And we're going to explain what those are as well. So to understand those dendrograms, we have to explain clustering. Clustering is a technique to group things that are close. We do this in our daily lives when we, for example, group animals into birds and reptiles and amphibians, et cetera. We do it in many other situations as well. It's very intuitive. But today, we're going to learn how to do it mathematically, because when we analyze data, we usually want to be able to write a program that can do this for us. So to group things that are close, we first need a definition of close. What does that mean? How can we make that mathematically formal? And then once we define what close means, then we're going to be able to describe some of the clustering algorithms. In genomics, the two most common things for which we try to find distances between are samples-- so we might want to find groups of tumors that behave similarly in their gene expression or some other outcome. We might want to find individuals that have similar genomes. But we can also find distances between genomic endpoints, like genes. So we might want to find which genes behave similarly across time points, for example. So we're going to start. We're going to do that and we're going to start just reviewing the basic definition of distance. The most common distance we use in data analysis is the Euclidean distance that we learn in high school. Just to review very quickly, you have two points. In a two-dimensional space, here are the two points, X1, Y1; X2, X2. And we want to know the distance between them. Basically what we do is we compute the length of the hypotenuse, which is given by this very well-known formula. Now in genomics, we rarely have data that's in two dimensions. Let's think about this for a second. Here is a subset of a table of gene expression that is a 22,215 by 189 table of gene expression. So if we were to compute the distance between two samples, say between sample number 3 and 1 sample number 4, what would be a point here? So a point could be considered to be the gene expression profile across all 22,000 genes. So now we are in 22,215 dimensions. We can't make a picture of that, obviously. We can make a picture of two, three, but past that it's quite difficult. But we can still define distance. And mathematically, it's quite simple. All you do is you apply the same formula. But now instead of adding two dimensions, you add all of them. So here's the formula for the distance between sample J and sample K, the Euclidean distance. We basically take the difference between the n tree and the i-th gene, so this is the i-th gene. But then we have two samples, J and K. So we see how close those two are. We square them. We take the sum of all the genes, all the dimensions, and then we take the square root. So that would define the distance between two samples. There's other ways to do it. This is the most basic one. We can also compute the distance between two genes. How would we do this? Well, we have several samples. So if we wanted to compute the distance between gene H and gene I, it's a very similar formula. We add up across all the samples how close the two genes are. And we keep the sample fixed. Here the sample's J. And we add across all samples. So now we're in a different space. We have n dimensions, where n is the number of genes. So if you wanted to compute this for one of your data sets, there's something important you should keep in mind. If you have a micro-array with 22,000 genes, or if you have an RNA-Seq experiment with hundreds of thousands of transcripts, or if you have a ChIP-Seq experiment with thousands of peaks, you're going to be computing many, many distances if you look at all the pairs. In the example we've been going through, where we have 22,000 and some genes, there's going to be over 200 million pairs of genes for which we can compute distance. That's something to keep in mind, because most computers will not be able to create a matrix that big. It might crash your R session. All right. So in the next module, we're going to see how we use distance in practical applications in genomics. And then we're going to move on to define clustering. 2 3