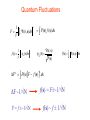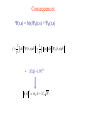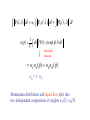Download pisa lecture 3

Lecture 3
BEC at finite temperature
Thermal and quantum fluctuations in condensate fraction.
Phase coherence and incoherence in the many particle wave function.
Basic assumption and a priori justification
Consequences
Connection between BEC and two fluid behaviour
Connection between condensate and superfluid fraction
Why BEC implies sharp excitations.
Why sf flows without viscosity while nf does not.
How BEC is connected to anomalous thermal expansion as sf is cooled.
Hoe BEC is connecged to anomalous reduction in pair correlations as sf is cooled.
Thermal Fluctuations
f (T )   j (T ) F j
At temperature T
j
Boltzman factor
exp(-Ej / T)/Zj
  2
1 
F j  n j (0)   ds   j (r , s )dr
V

f   j (T ) F j  f
2

2
j
Δf ~1/√N
Fj = f ± ~ 1/ √ N
Basic assumption;
(√f is amplitude of order parameter)
 E    g (E) (E)dE
j
j
j
g(E)
All occupied states give same
condensate fraction
η(E)
ΔE, Δf
~1/ √ N-1/2
Can take one “typical” occupied state
as representative of density matrix
E
As T changes band moves to different energy
“Typical” state gives different f
All occupied states gives same f to ~1/√N
Drop subscript j to simplify notation
Quantum Fluctuations
1
F
V
  (r, s)dr
V
1
f (s)    s (r )dr
V V
2
  P (s) f (s)ds
 S (r) 
(r, s)
P(s)
P(s)   (r, s) dr
F   P(s)F  f (s) ds
2
ΔF ~1/√N
F = f ±~1/√N
2
f(s) = F±~1/√N
f(s) ~ f ± 1/√N
2
V
width~ħ/L
BEC
n(p)
n(p)   S (r) exp( ip  .r )dr
 S (r)
2
Weight
f
to ~1/√N
for any
state and
any s
Delocalised function of r
(non-zero within volume > f V)
J. Mayers Phys. Rev. Lett. 84 314 (2000),Phys. Rev.B 64 224521, (2001)
 S(r )
Phase correlations in r over distances ~L
otherwise

S
(r )dr ~ 0
Phase coherent
Phase incoherent
rC
Condensate
No condensate
~1/rC
Temperature dependence
At T = 0 , Ψ0(r,s) must be delocalised over
volume ~ f0V and phase coherent.
For T > TB occupied states Ψj(r,s) must be
either localised or phase incoherent.
What is the nature of the wave functions of
occupied states for 0 < T < TB?
BASIC ASSUMPTION
Ψ(r,s) = b(s)Ψ0(r,s) + ΨR(r,s)
• Ψ0(r,s) is phase coherent ground state
• ΨR(r,s) is phase incoherent in r
• b(s)  0 as T  TB for typical occupied state
• ΨR(r,s)  0 as T  0
1.
2.
3
4.
Gives correct behaviour in limits T  TB, T  0
True for IBG wave functions.
Bijl-Feynman wave functions have this property
Implications agree with wide range of experiments
Bijl-Feynman wave functions
J. Mayers, Phys. Rev.B 74 014516, (2006)
 
 
 
(r , s )  (r , s )0 (r , s )
 


(r , s )  
exp(
ik
.
r
)


n 


k  n 1
N
nk
• nk = number of phonon-roton excitations with wave vector k.
•M = total number of excitations
• sum of NM terms.
M   nk
k
(r, s)  b(s)   R (r, s)
b(s) is sum of all terms not containing r = r1
Phase coherent in r.
Fraction of terms in b(s) is (1-M/N) as N  
M  N Θ(r,s) is phase incoherent (T  TB)
M  0 Θ(r,s) is phase coherent (T  0)
ΘR(r,s) is sum of terms containing r
Phase incoherent in r
rC ~1/Δk ~ 5 Å in He4 at 2.17K
Consequences
Ψ(r,s) = b(s)Ψ0(r,s) + ΨR(r,s)

2 1
1 
f   ds   (r , s )dr 
V
V


2
 b(s) ds  0 (r , s)dr
2
• If Δf ~1/N1/2
2
b( s )  wC  ~ 1 / N
Microscopic basis of two fluid behaviour
  2 
  2 
  2 

 (r , s ) dr  wC  0 (r , s ) dr   R (r , s ) dr  X (s ) ~ 1/ N

X (s ) 

 
0 (r , s )
 
R (r , s )
X
dr ~ 1 /
Macroscopic
System
  2 
  2 
  2 
 (r , s ) dr  wC  0 (r , s ) dr   R (r , s ) dr
N
  2 
  2 
  2 
 (r , s ) dr  wC  0 (r , s ) dr   R (r , s ) dr


  2
1 
n( p)   ds   (r , s ) exp( ip.r )dr
V
Parseval’s
theorem


 wC n0 ( p)  wR nR ( p)
wR = 1- wC.
Momentum distribution and liquid flow split into
two independent components of weights wC(T), wR(T).
E  wC E0  wR ER
Thermodynamic properties split into two independent
components of weights wc(T), wR(T)
SC  E0 T V  0
Bijl-Feynman wR determined by number of “excitations”
wc(T) = ρS(T)
wR(T) = ρN(T)
• True to within term ~N-1/2
• Only if fluctuations in f, ρS and ρN are negligible.
• Not in limits T 0 T  TB
f (T )   S (T ) f (0)
f (T )
f (0)
oo
T. R. Sosnick,W.M.Snow and P.E. Sokol Phys. Europhys Lett 9 707 (1989).
X X H. R. Glyde, R.T. Azuah and W.G. Stirling Phys. Rev. B 62 14337 (2000).
 E 
P  
   S P0   N PN
 V T
 (T )
 ( 0)
Superfluid has extra
“Quantum pressure”
PN = PB

  2 1
S (q )   i (r1 , s )
N
2

 
 exp( iq.rn ) dr1ds


  S S 0 (q )   N S R (q )

S (q )  1


S R (q )  1
SR-1
S  N  1
q
S-1
 (T )  1   S (T )[1   0 ]
α < 1 → S less ordered than SR
V.F. Sears and E.C. Svensson,
Phys. Rev. Lett. 43 2009 (1979).
α(T)
α0
 (T )  1   S (T )[1   0 ]
SR(q)  S0(q) → Ψ0(r,s) and ΨR(r,s)  0 for different s
Why is superfluid more disordered?
For s where Ψ0(r,s)  0
~7% free volume
Assume for s where ΨR(r,s)  0
negligible free volume
Ground state more disordered
Quantitative agreement with measurement at atomic size
and N/V in liquid 4He
J. Mayers Phys. Rev. Lett. 84 314 (2000)
Phase coherent component Ψ0(r,s)
s such that Ψ0(r,s)
is connected
 
 (r ).dr  2n (Macro loops)
Quantised vortices, macroscopic quantum effects
Phase incoherent component ΨR(r,s)
s such that ΨR(r,s) is not connected
Localised phase incoherent regions.
Localised quantum behaviour over length scales rC ~ 5 Å
No MQE or quantised vortices
Excitations
S (q,  ) 
1
N

2
A f (q)  (  E  E f )
f
Momentum transfer = ħq
Energy transfer = ħω
A f (q)  N   * (r, s) f (r, s) exp( iq.r )drds
|Aif(q)|2 has minimum width
Δq ~ 1/rC
Phase incoherent
Regions of size ~rC
Normal fluid - momentum of excitations is uncertain to ~ ħ/rC
Superfluid - momentum can be defined to within ~ ħ/L
0 < T < TB
ε
( deg K)
h/rC
q (Å-1)
Anderson and Stirling
J. Phys Cond Matt (1994)
Landau Theory
Basic assumption is that excitations with well defined
energy and momentum exist.
Only true in presence of BEC
Landau criterion vC = (ω/q)min
Normal fluid vC = 0
ω
q
Summary
BASIC ASSUMPTION
Ψ(r,s) = b(s)Ψ0(r,s) + ΨR(r,s)
Phase coherent
ground state
• Has necessary properties in limits T0, T  TB
• IBG, Bijl-Feynman wave functions have this form
•Simple explanations of
•Why BEC is necessary for non-viscous flow
Why Landau theory needs BEC.
Phase incoherent
Summary
Existing microscopic theory does not provide even qualitative
explanations of the main features of neutron scattering data
This is the only experimental evidence of the microscopic nature of
Bose condensed helium.
Theory given here explains quantitatively all these features
Why the condensate fraction is accurately proportional to the superfluid fraction
Why spatial correlations decrease as superfluid helium is cooled
Why superfluid helium is the only liquid which contains sharp excitations
Why superfluid helium expands when it is cooled