Download Circular motion and rotation Uniform circular motion

Dynamics of Uniform Circular Motion
Chapter 5
Learning ObjectivesCircular motion and rotation
Uniform circular motion

Students should understand the uniform circular motion of a particle, so they
can:
 Relate the radius of the circle and the speed or rate of revolution of the
particle to the magnitude of the centripetal acceleration.
 Describe the direction of the particle’s velocity and acceleration at any
instant during the motion.
 Determine the components of the velocity and acceleration vectors at
any instant, and sketch or identify graphs of these quantities.
 Analyze situations in which an object moves with specified
acceleration under the influence of one or more forces so they can
determine the magnitude and direction of the net force, or of one of
the forces that makes up the net force, in situations such as the
following:
• Motion in a horizontal circle (e.g., mass on a rotating merry-goround, or car rounding a banked curve).
• Motion in a vertical circle (e.g., mass swinging on the end of a
string, cart rolling down a curved track, rider on a Ferris wheel).
Table Of Contents
5.1 Uniform Circular Motion
5.2 Centripetal Acceleration
5.3 Centripetal Force
5.4 Banked Curves
5.5 Satellites in Circular Orbits
5.6 Apparent Weightlessness and Artificial Gravity
5.7 Vertical Circular Motion
Chapter 5:
Dynamics of Uniform Circular Motion
Section 1:
Uniform Circular Motion
Other Effects of Forces
 Up until now, we’ve focused on forces that speed up
or slow down an object.
 We will now look at the third effect of a force
Turning
 We need some other equations as the object will be
accelerating without necessarily changing speed.
DEFINITION OF
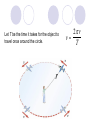
UNIFORM CIRCULAR MOTION
Uniform circular motion is the motion of an object
traveling at a constant speed on a circular path.
Let T be the time it takes for the object to
travel once around the circle.
r
2 r
v
T
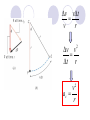
Example 1: A Tire-Balancing Machine
The wheel of a car has a radius of 0.29m and it being rotated
at 830 revolutions per minute on a tire-balancing machine.
Determine the speed at which the outer edge of the wheel is
moving.
1
 1.2 10 3 min revolution
830 revolution s min
T  1.2 10 3 min  0.072 s
2 r 2 0.29 m 
v

 25 m s
T
0.072 s
Newton’s Laws
 1st
 When objects move along a straight line the
sideways/perpendicular forces must be balanced.
 2nd
 When the forces directed perpendicular to velocity become
unbalanced the object will curve.
 3rd
 The force that pulls inward on the object, causing it to
curve off line provides the action force that is centripetal in
nature. The object will in return create a reaction force
that is centrifugal in nature.
Chapter 5:
Dynamics of Uniform Circular Motion
Section 2:
Centripetal Acceleration
In uniform circular motion, the speed is constant, but the
direction of the velocity vector is not constant.
    90

    90
 
v vt

v
r
v v

t
r
2
2
v
ac 
r
The direction of the centripetal acceleration is towards the
center of the circle; in the same direction as the change in
velocity.
2
v
ac 
r
Conceptual Example 2: Which Way Will the Object Go?
An object is in uniform circular
motion. At point O it is released
from its circular path. Does the
object move along the straight
path between O and A or along
the circular arc between points
O and P ?
Straight path
Example 3: The Effect of Radius on Centripetal Acceleration
The bobsled track contains turns
with radii of 33 m and 24 m.
Find the centripetal acceleration
at each turn for a speed of
34 m/s. Express answers as
2
multiples of g  9.8 m s .
ac  v 2 r
ac

34 m s 

 35 m s 2  3.6 g
ac

34 m s 

 48 m s 2  4.9 g
2
33 m
2
24 m
Chapter 5:
Dynamics of Uniform Circular Motion
Section 3:
Centripetal Force
Recall Newton’s Second Law
When a net external force acts on an object
of mass m, the acceleration that results is
directly proportional to the net force and has
a magnitude that is inversely proportional to
the mass. The direction of the acceleration is
the same as the direction of the net force.

a


F
m



F  ma
Recall Newton’s Second Law
 Thus, in uniform circular motion there must be a net
force to produce the centripetal acceleration.
 The centripetal force is the name given to the net
force required to keep an object moving on a circular
path.
 The direction of the centripetal force always points
toward the center of the circle and continually
changes direction as the object moves.
2
v
Fc  mac  m
r

Problem Solving Strategy
– Horizontal Circles
R
1. Draw a free-body diagram of the curving object(s).
2. Choose a coordinate system with the following two axes.
a) One axis will point inward along the radius (inward is
positive direction).
b) One axis will point perpendicular to the circular path (up is
positive direction).
3. Sum the forces along each axis to get two equations for two
unknowns.
a)  FRADIUS: +FIN  FOUT = m(v2)/ r
b)  F : FUP  FDOWN = 0
4. Do the math of two equations with two unknowns.

Just in case…
tan
R
 The third dimension in these problems would be a direction
tangent to the circle and in the plane of the circle.
 We choose to ignore this direction for objects moving at
constant speed.
 If an object moves along the circle with changing speed then
the forces tangent to the circle have become unbalanced.
 You can sum the tangential forces to find the rate at which
speed changes with time, aTAN.
 The linear kinematics equations can then be used to describe
motion along or tangent to the circle.
  FTAN: FFORWARD  FBACKWARD = m aTAN
Example 5: The Effect of Speed on Centripetal Force
The model airplane has a mass of 0.90 kg and moves at
constant speed on a circle that is parallel to the ground.
The path of the airplane and the guideline lie in the same
horizontal plane because the weight of the plane is balanced
by the lift generated by its wings. Find the tension in the 17 m
guideline for a speed of 19 m/s.
2
v
Fc  T  m
r

19 m s 
T  0.90 kg 
2
17 m
 19 N
5.3.1. A boy is whirling a stone at the end of a string around his head. The
string makes one complete revolution every second, and the tension in
the string is FT. The boy increases the speed of the stone, keeping the
radius of the circle unchanged, so that the string makes two complete
revolutions per second. What happens to the tension in the sting?
a) The tension increases to four times its original value.
b) The tension increases to twice its original value.
c) The tension is unchanged.
d) The tension is reduced to one half of its original value.
e) The tension is reduced to one fourth of its original value.
Chapter 5:
Dynamics of Uniform Circular Motion
Section 4:
Banked Curves
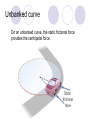
Unbanked curve
On an unbanked curve, the static frictional force
provides the centripetal force.
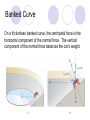
Banked Curve
On a frictionless banked curve, the centripetal force is the
horizontal component of the normal force. The vertical
component of the normal force balances the car’s weight.
2
v
Fc  FN sin   m
r
FN cos  mg
2
v
tan  
rg
Example 8: The Daytona 500
The turns at the Daytona International Speedway have a
maximum radius of 316 m and are steely banked at 31
degrees. Suppose these turns were frictionless. As what
speed would the cars have to travel around them?
2
v
tan  
rg
v
v  rg tan 
316 m 9.8 m

s 2 tan 31
v  43 m s 96 mph 
Chapter 5:
Dynamics of Uniform Circular Motion
Section 5:
Satellites in Circular Orbits
Don’t worry, it’s only rocket science
There is only one speed that a satellite can have if the
satellite is to remain in an orbit with a fixed radius.
2
v
mM E
Fc  m  G 2
r
r
GM E
v
r
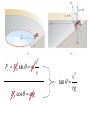
Example 9: Orbital Speed of the Hubble Space Telescope
Determine the speed of the Hubble Space Telescope orbiting
at a height of 598 km above the earth’s surface.
GM E
v
r
v
6.67 10
N  m kg 5.98 10 kg 
6
3
6.38 10 m  598 10 m
11
2
2
v  7.56 103 m s  16,900 mph
v  MACH 22
24
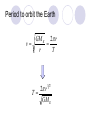
Period to orbit the Earth
GM E 2 r
v

r
T
2 r
T
GM E
32
Geosynchronous Orbit
2 r
T
GM E
32
T 2GM E
r3
2
2 
r3
T 2GM E
2 2
T  24 hours
3

11 m 
 5.9742 x10 24 kg
86,400s   6.67 x10
kg s 
3

r
2 2

2

rE  6.38 x106 m
r  4.22 x10 m
h  3.58x107 m  22,000 miles
7
Chapter 5:
Dynamics of Uniform Circular Motion
Section 6:
Apparent Weightlessness and Artificial Gravity
Conceptual Example 12: Apparent Weightlessness and
Free Fall
In each case, what is the weight recorded by the scale?
Example 13: Artificial Gravity
At what speed must the surface of the space station move
so that the astronaut experiences a push on his feet equal to
his weight on earth? The radius is 1700 m.
2
v
Fc  m  mg
r
v  rg

1700 m9.80 m s 2 
v  130 m s
Chapter 5:
Dynamics of Uniform Circular Motion
Section 7:
Vertical Circular Motion
Circular Motion
 In the previous lesson the radial and the perpendicular forces
were emphasized while the tangential forces were ignored.
Each class of forces serves a different function for objects
moving along a circle.
Class of Force
Purpose of the Force
Radial Forces
Curves the object off a straight-line path.
Perpendicular Forces
Holds the object in the plane of the circle.
Tangential Forces
Changes the speed of the object along the circle.
Circular Motion
 Most of the horizontal, circular problems occurred at
constant speed so that we could ignore the
tangential forces. The vertical, circular problems
have objects moving with and against gravity so that
speed changes. Tangential forces become
significant. The good news is that perpendicular
forces can now be ignored unless hurricanes are
present.
Problem Solving Strategy for Vertical Circles
1. Draw a free-body diagram for the curving objects.
2. Choose a coordinate system with the following two axes.
a) One axis will point inward along the radius.
b) One axis points tangent to the circle in the circular plane, along the direction
of motion.
3. Sum the forces along each axis to get two equations for two unknowns.
a)  FRADIUS: +FIN  FOUT = m(v2)/ r b)  FTAN : FFORWARD  FBACKWARDS = ma
4. You can generally expect the weight of the object to have components in both
equations unless the object is exactly at the top, bottom or sides of the circle.
5. If the object changes height along the circle you may need to write a
conservation of energy statement. This goes well with centripetal forces since
there is an {mv2} in both kinetic energy terms and in centripetal force terms.
6. Do the math with 3(a) and 4 or perhaps 3(a) and 3(b).
Minimum/Maximum Speed Problems
 Sometimes the problem addresses “the minimum speed”
that an object can move through the top of the circle or
“maximum speed” that an object can move along the top of
the circle.
 If the bucket of water turns too slowly you get wet.
 If a car tops a hill too quickly it leaves the ground.
 Allowing v2/r to equal g can solve many of these questions.
 By solving for v you will find a critical speed.
FC  FW
mv 2
 mg
r
v  rg
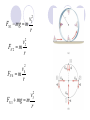
Conceptual Example: A Trapeze Act
In a circus, a man hangs upside down from a trapeze, legs
bent over and arms downward, holding his partner. Is it harder
for the man to hold his partner when the partner hangs
straight down and is stationary of when the partner is swinging
through the straight-down position?
2
1
v
FN 1  mg  m
r
FN 2
FN 4
2
2
v
m
r
2
4
v
m
r
2
3
v
FN 3  mg  m
r