Download 8.6 Notes - Trapezoids

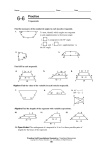
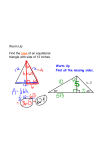
8.6 Trapezoids
Objectives

Recognize and apply properties of
trapezoids

Solve problems using the medians of
trapezoids
Trapezoids
A trapezoid is a
quadrilateral with exactly
one pair of parallel sides.
 The parallel sides are
called the bases.
 A trapezoid has two
pairs of base angles. In
trapezoid ABCD, D and
C are one pair of base
angles. The other pair is
A and B.
 The nonparallel sides of
the trapezoid are called
the legs.

Trapezoids
If the legs of a trapezoid are ≅, then it is called
an isosceles trapezoid.
Theorem 8.18: Both pairs of base
s of an isosceles trapezoid are ≅.
(A ≅ B and C ≅ D)
Theorem 8.19: The diagonals of an
isosceles trapezoid are ≅.
(AC ≅ BD)
Example 1:
Write a flow proof.
Given: KLMN is an isosceles
trapezoid.
Prove:
Example 1:
Proof:
Your Turn:
Write a flow proof.
Given: ABCD is an isosceles trapezoid.
Prove:
Your Turn:
Proof:
Example 2:
The top of this work station appears to be two adjacent
trapezoids. Determine if they are isosceles trapezoids.
Each pair of base angles is congruent, so the legs are the
same length.
Answer: Both trapezoids are isosceles.
Your Turn:
The sides of a picture frame appear to be two adjacent
trapezoids. Determine if they are isosceles trapezoids.
Answer: yes
Example 3a:
ABCD is a quadrilateral with vertices A(5, 1), B(–3, –1),
C(–2, 3), and D(2, 4). Verify that ABCD is a trapezoid.
A quadrilateral is a trapezoid if exactly one pair of opposite
sides are parallel. Use the Slope Formula.
Example 3a:
slope of
slope of
slope of
slope of
Answer: Exactly one pair of opposite sides are parallel,
So, ABCD is a trapezoid.
Example 3b:
ABCD is a quadrilateral with vertices A(5, 1), B(–3, 1),
C(–2, 3), and D(2, 4). Determine whether ABCD is an
isosceles trapezoid. Explain.
Example 3b:
First use the Distance Formula to show that the
legs are congruent.
Answer: Since the legs are not congruent, ABCD is not
an isosceles trapezoid.
Your Turn:
QRST is a quadrilateral with vertices Q(–3, –2), R(–2, 2),
S(1, 4), and T(6, 4).
a. Verify that QRST is a trapezoid.
Answer: Exactly one pair of opposite sides is parallel.
Therefore, QRST is a trapezoid.
b. Determine whether QRST is an isosceles trapezoid.
Explain.
Answer: Since the legs are not congruent, QRST
is not an isosceles trapezoid.
Medians of Trapezoids


The segment that joins the
midpoints of the legs of a trapezoid
is called the median (MN). It is
also referred to as the
midsegment.
Theorem 8.20: The median of a
trapezoid is || to the bases and its
measure is ½ the sum of the
measures of the bases.
BC || AD
MN = ½ (BC + AD)
median
Example 4a:
DEFG is an isosceles trapezoid with median
DG if
and
Find
Example 4a:
Theorem 8.20
Substitution
Multiply each side by 2.
Subtract 20 from each side.
Answer:
Example 4b:
DEFG is an isosceles trapezoid with median
Find
, and
if
and
Because this
is an isosceles trapezoid,
Example 4b:
Consecutive Interior Angles Theorem
Substitution
Combine like terms.
Divide each side by 9.
Answer:
Because
Your Turn:
WXYZ is an isosceles trapezoid
with median
a.
Answer:
b.
Answer:
Because
Assignment

Pre-AP Geometry
Pg. 442 #9 – 19, 22 – 28, 32, 34

Geometry:
Pg. 442 #9 – 18, 22 - 28