Download Government Expenditure Composition and Growth in Chile

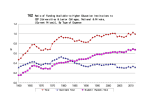
Government Expenditure Composition and Growth in Chile
November 30, 2006
Carlos J. García
Santiago Herrera
Jorge E. Restrepo
I.
Introduction
The purpose of this paper is to examine and quantify the impact on growth of alternative
budgetary compositions, with a model that captures some of the specific stylized facts of
the Chilean Economy. We also want to test the effects of larger social security payments
if the pension system is actually reformed as the current administration promised.
Total public spending as a share of GDP has evolved through time and across regions
with little or no relationship with growth rates, at least since the 1980’s. Table 1 shows
the decadal average of total public spending (ratio to GDP) and average per-capita
growth rates in the different decades since 1980. In general, the public spending ratio is
decreasing, while growth rates show diverse behavior: stable (EAP), increasing (MNA), a
high-low-high pattern (AFR), or a low-high-low pattern (LAC). The only region (SAS)
with a clear rising trend in the spending ratio shows a decreasing trend in growth rates,
though it is the highest of the whole sample.
On the other hand, the composition of public expenditure has varied significantly with
clear patterns across regions and through time. One of the trends is the rising share of
interest payments in almost all the regions (Figure 1). Another notable trend is the rising
importance of social security payments. Developing regions, more specifically, AFR,
ECA, and LAC, experienced substantial increase in public spending on social security in
the last decades. Finally, agriculture spending and transport and communication are
decreasing in importance within central government budgets (Table 2).
Chile is an exception regarding some of the features above mentioned. For instance, as a
percentage of GDP, interest payments as well as defense expenditures and social security
payments have declined steadily between 1990 and 2005. Moreover, spending on
transportation, education and health has augmented since 1990 (Table 3).
Figure 1 Interest Payment as Percent of Total Expenditure
20
18
16
14
12
10
8
6
4
2
AFR
EAP
ECA
INL
LAC
MNA
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987
1986
1985
1984
1983
1982
1981
1980
0
SAS
Data Source: IMF Government Finance Statistics
In order to reach the goals of the article we calibrate for Chile a model originally
developed by Glomm and Rioja (2003), later on modified by Herrera and Pang (2005).
Table 1 Total Expenditure and GDP per capita Growth
Total Exp (% of GDP)
GDP p.c. Growth (%)
AFR
EAP
ECA
INL
LAC
MNA
SAS
1980's 1990's 2000's 1980's 1990's 2000's 1980's 1990's 2000's 1980's 1990's 2000's 1980's 1990's 2000's 1980's 1990's 2000's 1980's 1990's 2000's
28.3 27.2 23.1 25.1 22.3 21.8 37.9 33.5 29.4 36.8 37.1 29.2 25.2 21.7 21.9 34.9 30.0 29.0 25.6 24.7 27.3
0.6
-0.6
0.7
2.5
2.5
2.4
1.8
1.0
5.5
2.3
2.0
1.9
0.1
1.8
0.2
-0.5
1.2
2.1
3.5
3.3
2.0
AFR – Africa, EAP – East Asia and Pacific, ECA – East Europe and Central Asia, INL – Industrialized Countries, LAC – Latin America and Caribbean, MNA –
Middle East and North Africa, SAS – South Asia.
Source: World Bank World Development Indicators and IMF Government Finance Statistics
Table 2 Composition of Total Expenditure (%, consolidated central government)
AFR
EAP
ECA
INL
1980 1998 2001 1980 1998 2001 1980 1998 2001 1980 1998
Agriculture
6.7 4.8 4.6 9.7 4.9 2.4 3.1 3.3 2.9 3.8 2.6
Education
12.8 13.9 14.7 14.1 12.5 13.4 5.7 6.6 6.4 8.5 7.9
Health
4.2 5.3 8.4 5.4 5.6 7.1 1.4 8.6 8.8 9.0 10.3
T&C
7.3 2.3 6.1 11.7 7.9 4.5 4.0 4.1 4.2 5.9 3.6
Social Security
3.4 5.8 21.4 3.2 6.7 12.1 7.7 32.2 35.0 34.9 34.2
Defense
8.8 9.1 0.8 18.8 13.6 8.3 23.0 6.1 5.2 8.5 6.6
Order & Safety
0.0 4.6 7.2 0.7 4.8 7.0 0.0 5.8 6.0 0.5 2.8
Fuel & Energy
1.3 0.4 0.1 2.0 0.9 1.0 2.0 0.6 0.8 0.8 0.5
Mining & Manuf.
2.0 2.6 0.7 2.5 0.4 0.5 14.1 1.2 0.4 1.5 1.0
Public Service
18.2 14.7 9.8 14.5 10.3 10.2 10.3 5.7 6.4 7.3 5.9
Housing
1.5 1.6 6.6 2.7 5.4 3.9 1.5 1.3 1.1 2.4 2.5
Recreation
1.3 0.6 1.3 0.7 2.8 2.1 0.1 1.8 1.6 1.0 1.3
Other
32.3 34.4 18.3 13.8 24.2 27.6 27.1 22.7 21.0 15.8 20.8
Source: Calculated using data from IMF Government Finance Statistics
2001
1.4
6.0
12.1
2.1
34.2
12.9
2.9
0.1
0.6
6.1
2.9
0.9
17.8
1980
5.5
12.5
8.0
7.4
14.0
6.5
0.4
1.8
1.9
15.4
2.9
0.7
22.8
LAC
1998
2.3
15.7
9.1
3.9
23.8
4.5
5.7
0.9
0.7
8.5
3.4
0.5
21.0
2001
1.5
17.4
10.9
3.9
24.1
4.2
6.5
0.4
0.6
7.8
3.2
0.6
18.8
1980
4.9
12.8
4.7
5.1
6.1
17.7
0.0
5.1
3.8
11.8
5.4
3.0
19.5
MNA
1998
5.3
15.0
5.2
2.9
9.5
14.7
7.8
5.8
1.4
10.1
3.1
2.1
17.1
2001
0.5
13.3
7.8
2.7
7.5
15.2
12.2
0.3
0.3
29.5
3.7
0.5
6.3
1980
8.1
5.2
3.1
18.2
3.6
11.8
0.0
3.9
3.6
11.8
3.6
0.6
26.7
SAS
1998
4.6
10.3
6.1
7.9
3.8
12.3
4.1
6.5
0.8
9.9
5.3
0.4
28.1
2001
3.8
9.3
5.0
6.3
3.6
11.1
3.9
9.0
0.5
12.1
4.3
0.2
31.0
Note:
1. T & C stands for transportation and communication.
2. AFR – Africa, EAP – East Asia and Pacific, ECA – East Europe and Central Asia, INL – Industrialized Countries, LAC – Latin America and Caribbean,
MNA – Middle East and North Africa, SAS – South Asia.
Table 3. Composition of Central Government Expenditure
(% of GDP)
1990
1996
2005
Agricultura y otros
1.2
1.2
0.9
Defense
2.3
1.5
1.3
Education
2.3
2.8
3.3
Environment
0.0
0.1
0.1
Order & Law
0.9
1.0
1.3
Health
1.9
2.4
2.9
Housing
0.9
1.1
1.0
Public Service
2.8
1.4
1.3
Recreation
0.1
0.1
0.1
Social Security
7.4
6.4
5.8
Transporte
0.8
1.6
1.7
Otros
0.1
0.0
0.1
Source: Estadísticas de las finanzas públicas:Ministerio de HaciendaDIPRES
The second section presents the model. In the third has the calibration of the model. The
fourth section includes the experiments. Finally, the fifth section has the conclusions.
2. The Framework of General Equilibrium
The model was developed by Glomm-Rioja (2004) for Brazil, but here we modify
it to include additional types of expenditure (maintenance of public capital) and changes
in the calibration parameters. The building blocks of the model are defined by the
preferences, the technology, and the resource constraints, described in detail in the
remainder of this section. Three crucial features are 1) On the preferences side,
consumption and leisure decisions are made by agents differentiated by their generation:
they study when young, work in adulthood, and receive transfers (social security)
payments when old This is essential to model the social security transfers; 2)
Government expenditure is productive (in infrastructure and education) and unproductive
(transfer payments to the old), affecting production and consumption decisions; 3)
Interest rates depend on the size of public debt.
2.1. Preferences
Each generation of households lives for three periods: youth, adulthood and
retirement. Each individual, when young, is endowed with one unit of time which can be
allocated to learning nt or leisure ( 1  nt ) . During adulthood the individual supplies
labor inelastically, and allocate labor income between current consumption and savings.
4
When retired the individual lives on transfers and returns on savings. Specifically,
preferences are given by1
ln( 1  nt )  ln ct , t   ln ct , t 1
(1)
where ct , s denotes consumption of generation t (those becoming adults at the beginning
of period t) in time period s, s = t, t+1.
The wage-earning ability of the adult is determined by the effectiveness of labor
or human capital, ht , which, in turn, is determined by : a) the learning time, nt ; b) public
spending on education, Et 1 ; and, c) parental human capital level, ht 1 . Specifically, the
evolution of human capital follows the rule below.
ht  Bnt Et1ht1 , 0   ,  ,   1,
B0
(2)
The utility maximization problem is solved recursively, starting with the problem
faced by adults. At this stage the learning/schooling decision has been made and thus the
stock of human capital ht is given. The representative adult in generation t solves the
following problem, taking as given the factor prices and fiscal policy parameters.
max
ln ct , t   ln ct , t 1
ct , t  st  (1   L, t ) wt ht
ct , t 1  (1  (1   K , t )rt 1 ) st  Tt 1
s.t.
(3)
given
( wt ,rt 1 , L ,t , K ,t ,Tt 1 ,ht ) ,
where s is savings for retirement, w the real wage rate, r net real interest rate,  L tax
rate on labor income,  K tax rate on capital income, and T the transfer payments
received during old age.
A little manipulation of the first order conditions yields the savings decisions given by
st 

1 
Tt 1
1  1 (1 K ,t 1 ) rt 1
(1   L, t ) wt ht  1
(4)
The important thing to note is that (expected) future transfers affect current savings
decisions.
To simplify the notations, we denote after tax factor prices as follows.
~
~  (1   ) w . Replacing the optimal savings (equation (4) )
rt 1  (1   K ,t 1 )rt 1 and w
t
L ,t
t
into the objective function in the consumer’s problem (3) yields an indirect utility
function for the adult, which is of the following form

~ h  T   ln (1   )(1  ~
(5)
(1   ) ln (1  ~
rt 1 ) w
rt 1 )   ln(
)
t t
t 1
1 
The problem for the young is hence to maximize (5) with respect to learning time, nt ,
subject to the law of motion for human capital in (2).
.
The solution to this problem is defined by the following nonlinear equation
1
The utility function can be augmented to include utility from consumption of a public good, P. This good
does not affect production or consumption decisions, and hence is generally omitted.
5
~ Bn  E  h   T   (1   )(1  ~
~ Bn  1 E  h 
(1   (1   ))(1  ~
rt 1 ) w
rt 1 ) w
t
t
t 1 t 1
t 1
t
t
t 1 t 1
(6)
2.2. Production
The aggregate production technology for the single non-storable consumption
good is given by
 1
Yt  AG
, 0   ,   1,
t Kt H t
A0
(7)
where Yt , Gt , K t , H t are, in order, aggregate output, publicly provided infrastructure
capital, private physical capital and human capital. The technology exhibits constant
returns to scale in the private factors.
Public infrastructure capital evolves according to
Gt 1  (1   G (mt ))Gt  I G ,t
(8)
where  G (mt ) is the rate of depreciation defined as a declining function of maintenance
as percent of GDP, mt . For simplicity, a linear functional form for depreciation is
assumed, i.e.  G (mt )  1  mt . I G ,t is the public investment in infrastructure.
Infrastructure is a public good completely financed by the government. The private
physical capital evolves according to
K t 1  (1   K ) K t  I K ,t
(9)
where  K is the rate of depreciation of private physical capital, and I K ,t is private
investment financed by private savings.
The representative firm maximizes profits, taking as given the market factor prices.
Perfect competition dictates that the firm will employ labor and rent private capital up to
the point that marginal product value equals marginal factor cost. Specifically,
wt  (1   ) HYtt
(10)
qt   KYtt  (1   K )
where qt is the rental rate of capital. The no-arbitrage condition holds for the capital
market: 1  rt  qt . That is, rt   K  
Yt
Kt
. The firm’s profits maximization conditions in
(10) imply that private physical capital will evolve according to the following path.
1

1
K t 1  (A) 1 Gt11 H t 1 (rt 1   K )  1
(11)
2.3. Fiscal Policy
The government provides public goods, which is financed either by tax revenue or
by borrowing. That is, the government spends G ,t percent of GDP on investment in
infrastructure in period t,  M ,t on maintenance (note mt   M ,t ),  E ,t on education,  T ,t
on transfers, and  P,t on other general public services (non-utility enhancing). The
government collects taxes on labor income at rate  L ,t and on capital (interest) income at
rate  K ,t . It can also choose to raise debt to finance spending. Formally, the government
budget constraint is given by
Dt 1   L ,t wt H t   K ,t rt K t  ( G ,t   M ,t   E ,t   T ,t   P ,t )Yt  (1  rt (1   K ,t )) Dt (12)
6
where Dt is the government stock of debt at time t and can be held by domestic agents or
foreigners.
2.4. Competitive Equilibrium
A macroeconomic equilibrium is defined by the following system, where
uppercase letters indicate aggregate variables.
1. The household utility maximization problem is solved. That is, conditions (4) and (6)
hold.
2. The representative firm’s profits maximization problem is solved. That is, condition
(10) holds.
3. The government budget constraint (12) is satisfied.
4. The goods market clears: Ct  S t  Taxt  Yt  (1   K ) K t
5. The competitive input market for human capital (labor) clears: H t   ht
6. The interest rate is determined as suggested by Schmitt-Grohe and Uribe (2003), with
a debt elastic interest rate as follows:
rt  r *  R( DYtt )
(13)
where r * is the world prevailing interest rate, and R is an increasing function of debt
level with R( 0 )  0 and R' 0 . For simplicity, a linear mark-up function for spreads is
assumed, R( DYtt )  
Dt
Yt
. In this case private savings are adjusted accordingly to prevailing
interest rate, as implied in equation (4). In equilibrium domestic savings are either rented
to the private firm or invested in government bonds, with any fiscal financing gap soaked
up by foreign investors.
This interest equation, together with the laws of motion for infrastructure capital
(condition 8), for private physical capital (condition 11) and for human capital (2) fully
determines the equilibrium trajectory for GDP.
3. Calibration
The model is calibrated based on public expenditure data of the Chilean economy, and
parameters that can characterize the Chilean economy but can also describe other
economies. These parameters can be altered and the last section presents sensitivity
analysis variations in some of the parameter values.
The benchmark parameter values are listed in Table 3.
Table 3 Benchmark Parameter Values
Discount Factor (  )
Total Factor Productivity (  )
(.973)30
13.0, calibrated to get balanced growth
7
Human Capital parameter ( B )
Capital’s Share of GDP (  )
Public Capital Elasticity ( )
Public Education Expenditure Elasticity (  )
Interest rate sensitivity to public debt (  )
Learning Time Elasticity (  )
Parental Human Capital Elasticity (ρ)
Depreciation parameter - public capital (  )
Depreciation rate - private capital (  K )
3.87, calibrated to get balanced growth
0.5
0.3
0.1
0.04
0.137, calibrated to get n  .15
0.75, calibrated to get balanced growth
4.0, to match 10% depreciation per
annum
10% per annum
Tax Revenue as a fraction of GDP (Tax)
Transfers as a fraction of GDP ( T )
Public Education Expenditure ( E )
Public Capital Expenditure ( G )
Public Expenditure on Maintenance ( M )
Non-utility enhancing Public Expenditure ( P )
Labor income tax rate (  L )
Capital income tax rate (  K )
20.5%
8%
6.3%
1.0%
1.0%
4.2%
20%
World Interest Rate ( r * )
5.58%
17%
The value of the subjective discount factor,  , has been traditionally taken to be less
than unity, although empirical evidence has suggested a wide range around unity2. For
instance, Annicchiarico and Giammarioli (2004) use a low value, 0.74, while Hubbard
and Judd (1987) set   0.985 in a representative agent, life cycle model, which, in
addition, models explicitly lifetime uncertainty (mortality). In the current deterministic
overlapping generations model, it is reasonable to assume a slightly lower discount
factor, i.e. 0.973 per annum, or (0.973)30 per model period.
The estimate for private capital’s share of national income (.5) corresponds to Chile’s
figures. It is also the mid-point in the range of Latin American countries reported by De
Gregorio (1992).
The public capital elasticity  (.3) is similar to the value reported by Arestoff and
Hurlin (2005) for the larger developing countries in his sample. The public expenditure
elasticity in the learning technology, μ, uses a value of 0.1, estimated for the U.S.
economy by Card and Krueger (1992). This value may understate the contribution of
2
For instance, Auerbach and Kotlikoff (1987) set discount factor to be 0.985 and Hurd (1989) gives
estimate of 1.011 with additional mortality risk.
8
public expenditure to human capital accumulation for developing countries according to
Betts (1996), presumably because public education expenditures may be more effective
when average income is lower.
The learning time elasticity,  , is chosen so that individuals spend 15% of
available hours learning.3 The parameter value on parental human capital in the learning
technology, ρ, is calibrated in order to reach balanced growth.
The Statistics from the governemnt are used to calculate the public expenditure
compositions summarized in Table 1. Total tax revenue as a fraction of GDP is on
average 20.5%, among which 8% is allocated to transfers, 6.3% to public education, 1%
to infrastructure investment, 1% to maintenance , and 4.2% to non-utility-enhancing
public services. The labor and capital tax rates in benchmark are set to 20% and 17%,
respectively.
The world interest rate is set to be 6% annually. The mark-up elasticity for spreads,  , is
set to 0.04 following the estimates for Latin America in Eichengreen and Mody (1998),
where it is found that the logarithm of spreads increases by 1.37 if debt-GNP ratio
increases by one percentage point. Given the regional average of spreads (about 400 basis
points), it is expected that the spreads will widen by 548 basis points (548 = 1.37*400).
Thus a parameter of the order of .0.04 or 0.05 is chosen as a moderate benchmark. The
last section provides sensitivity analysis on this parameter.
The depreciation rate parameter for public capital,   4 , is calibrated as follows. Given
an average of 10 percent for the yearly depreciation rate of public capital in developing
countries (Rioja, 2003), only 4 percent of original public capital survives after one model
period (30-years) Using 1 percent of GDP as the benchmark maintenance expenditure, 4
is calibrated to give depreciation rate 0.96.
Private capital is assumed to depreciate at the same speed as public capital does in
benchmark case, i.e.  K  0.96 .
4. Policy Experiments
The overlapping generations model is solved recursively with market equilibrium
realized in each period. The steady state is defined as the case where a constant, balanced
growth rate is achieved (5% in this case). Against this benchmark, various policy
experiments are carried out in period zero.
4.1 Permanent/Temporary Increase in Expenditure. Tables 4 and 5 as well as Figures
2 and 3 show the following main results:
a. The permanent increase in any type of spending has a higher impact on growth when it
is financed with higher taxes (Table 4).
3
The rationale is as follows according to Glomm and Rioja (2004). Schooling on average involves about 6
hours of school work per day during a 200 day school year. This yields a percentage of total time spent on
schooling at about (6x200)/(24x365)=15%.
9
b. The expenditure with higher impact on growth is infrastructure spending, followed by
education. Compared with the benchmark growth rate, (or GDP level) the other two types
of spending lead to lower output (Table 4).
.
c. The transitory increase in expenditure yields qualitatively similar results, but in terms
of the comparison between the selected financing mechanism (debt vs. taxes), the
contrast is sharp. For instance, the growth impact of infrastructure spending financed by
taxes is superior to the debt-financed increase (Table 5).
Table 4. GDP growth rate after a permanent increase in expenditure (1% of GDP)
Period
1
2
3
4
5
Financed by Debt
Financed by Tax
Benchmark Transfer Education Infrastructure Maintenace Transfer Education Infrastructure Maintenace
4.97
4.968
5.044
5.981
4.984
4.968
5.042
5.979
4.982
5.00
5.005
5.017
4.726
4.999
5.003
5.018
4.727
5.000
5.01
5.012
5.015
4.956
5.011
5.011
5.014
4.956
5.011
5.01
5.013
5.014
5.002
5.013
5.013
5.014
5.002
5.013
5.01
5.013
5.014
5.011
5.013
5.013
5.013
5.011
5.013
Figure 2. Permanent increase in expenditure (1% of GDP)
5.90
5.90
5.70
5.70
5.50
5.50
5.30
5.30
5.10
5.10
4.90
4.90
4.70
4.70
4.50
4.50
1
2
3
Benchmark
Transfer
Infrastructure
Maintenace
4
1
5
Education
2
3
Benchmark
Transfer
Infrastructure
Maintenace
4
5
Education
Table 5 GDP Growth Rate after a temporary increase in expenditure (1% of GDP)
Period
1
2
3
4
5
Financed by Debt
Financed by Tax
Benchmark Transfer Education Infrastructure Maintenace Transfer Education Infrastructure Maintenace
4.97
4.968
5.044
5.981
4.984
4.968
5.042
5.979
4.982
5.00
5.005
5.017
4.726
4.999
5.003
5.018
4.727
5.000
5.01
5.012
5.015
4.956
5.011
5.011
5.014
4.956
5.011
5.01
5.013
5.014
5.002
5.013
5.013
5.014
5.002
5.013
5.01
5.013
5.014
5.011
5.013
5.013
5.013
5.011
5.013
10
Figure 3 Temporary increases in expenditure (1% of GDP)
6.10
5.90
5.90
5.70
5.70
5.50
5.50
5.30
5.30
5.10
5.10
4.90
4.90
4.70
4.70
4.50
4.50
1
2
3
Benchmark
Transfer
Infrastructure
Maintenace
4
1
5
Education
2
3
Benchmark
Transfer
Infrastructure
Maintenace
4
5
Education
4.1 Permanent reallocation of Expenditures
This experiment tests the effects of a permanent increase in social security payments as a
result of the pension reform currently under way in Chile.
To be written
5. Conclusions and future work
The overlapping generations model (OLG) used in this paper focuses on long run growth
trajectories, assume two-period deterministic life cycle for agents, i.e. certain death at
certain age. This setup facilitates the analytical derivation of equilibrium and policy
implication. It is a useful first step in quantifying the impact on long run growth and
income per capita of alternative budget compositions capturing two key elements that
have shaped budget composition in many countries over the last decades: the growing
importance of social security payments and rising interest payments as a share of total
expenditure.
The paper’s results provide quantitative evidence supporting the hypothesis of the
importance of public investment in achieving higher per-capita income in the long run. It
also provides evidence of the cost, in terms of growth, of increasing social security
payments because of the crowding out of productive expenditure (in education or
infrastructure).
The model however has several limitations.
11
The first limitation arises from the assumption of a constant elasticity of public capital,
which might overstate the productiveness of public capital. It would be more realistic to
model a non-linear elasticity such that productivity of public capital decreases as the
amount of investment increases. Alternatively, it could be useful to model an
“efficiency” of investment function, such that not all public investment is transformed
into public capital.
Another complication that could be added in extensions of this paper refers to the cost of
taxation. If administrative cots of taxation are added, such that the marginal cost of tax
revenues is increasing, then some of the conclusions regarding the preference of taxes
over debt might be overturned.
Future extensions of this paper could include public health expenditures that enhance
human capital.
12
References
Agenor, P.-R., 2004, Infrastructure, Public Education and Growth with Congestion Costs.
Manuscript.
Ai, C. and S. Cassou, 1995, A normative analysis of public capital. Applied Economics
27, 1201-1209.
Annicchiarico, Barbara and Incola Giammarioli, 2004, Fiscal Rules and Sustainability of
Public Finances in an Endogeneous Growht Model. European Central Bank Working
Paper Series No. 381.
Arestoff, Florence and Christophe Hurlin, 2005. Threshold Effects in the Productivity of
Public Capital in Developing Countries. Memeo.
Aschauer, D., 1989, Is public expenditure productive? Journal of Monetary Economics
23, 177-200.
Baier, S., J. Bergstrand and G. Glomm, 2003, Can Tax Cuts and Public Investment in
Education Influence Long-run Growth? Manuscript.
Baier, S. L. and G. Glomm, 2001, Long-run growth and welfare effects of public policies
with distortionary taxation. Journal of Economic Dynamics and Control 25, 2007-2042.
Barro, R., 1990, Government spending in a simple model of endogenous growth. Journal
of Political Economy 98, S103-S125.
Baxter, Marianne and Robert King, 1993, Fiscal Policy in General Equilibrium, the
American Economic Review, Vol. 93, No. 3 pp.315-334.
Betts, J., 1996, Is there a link between school inputs and earnings? Fresh scrutiny of an
old literature, in Burtless, G. ed. Does Money Matter? The effect of school resources on
student achievement and adult success. Washington, D.C. Brookings Institution Press.
Blanco, Fernando and Santiago Herrera, 2003, The quality of Chileian fiscal adjustment,
1999-2001. Working Paper, The World Bank.
Canning, D., 1999, The contribution of infrastructure to aggregate output, World Bank
Policy Research Paper no. 2246, Washington, DC.
___________, 1998, A database of world stocks of infrastructure, 1950-1995, World
Bank Economic Review 12, no.3. 529-547.
Canning, D. and E. Bannathan, 2000, The Social Rate of Return to Infrastructure
Investments, World Bank Development Research Group, Working Paper #2390.
13
Canning, D. and M. Fay, 1993, The effect of transportation networks on economic
growth. Columbia University Working Paper.
Card, D. and A. Krueger, 1992, Does school quality matter? returns to education and the
characteristics of public schools in the United States. Journal of Political Economy 100,
1-40.
Cassou, S. and K. Lansing, 2001, Tax Reform and Public-Sector Investment in Human
Capital, Manuscript.
, 1998, Optimal fiscal policy, public capital, and the productivity
slowdown, Journal of Economic Dynamics and Control 22, no.6, 911-935.
Chatterjee, S., G. Sakoulis and S. Turnovsky, 2003, Unilateral capital transfers, public
investment and economic growth. European Economic Review 47, 1077-1103.
Demetriades, P. O. and T. P. Mamuneas, 2000, Intertemporal output and employment
effects of public infrastructure capital: evidence from 12 OECD economies, The
Economic Journal 110, no. 465, 687-712.
Dornbush, Rudiger and Sebastian Edwards, eds., 1991, The Macroeconomics of
Populism in Latin America, The University of Chicago Press: Chicago, IL.
Easterly, W. and S. Rebelo, 1993, Fiscal policy and economic growth: an empirical
investigation, Journal of Monetary Economics 32, 417-458.
Edwards, S., 1984, LDC Foreign Borrowing and Default Risk: An Empirical
Investigation 1976-80. The American Economic Review 74, 726-734.
Eichengreen, B. and A. Mody, 1998, What Explains Changing Spreads on EmergingMarket Debt: Fundamentals or Market Sentiment. NBER Working Paper #6408.
Elias, V., 1992, Sources of growth: a study of seven Latin American economies. ICS
Press, San Francisco, CA.
Favero, C. and F. Giavazzi, 2002, Why are Chile’s Interest Rates so High? Manuscript.
Fay, M., 2001, Financing the Future: Infrastructure needs in Latin America, 2000-05.
Working Paper no. 2545, The World Bank.
Fischer, W. H. and S. Turnovsky, 1995, The Composition of Government Expenditures
and its Consequences for Macroeconomic Performance. Journal of Economic Dynamics
and Control 19, 747-786.
Glomm, G. and B. Ravikumar, 1994, Public Investment in Infrastructure in a Simple
Growth Model, Journal of Economic Dynamics and Control.
14
Glomm, G. and B. Ravikumar, 1998, Flat-Rate Taxes, Government Spending on
Education, and Growth, Review of Economic Dynamics.
Gregorio, Jose De, 1992. Economic Growth in Latin America. Journal of Development
Economics 39, pp.59-84.
Holtz-Eakin, D., 1994, Public Sector Capital and the Productivity Puzzle, Review of
Economics and Statistics 76, 12-21.
Holtz-Eakin, D. and A.E. Schwartz, 1995, Infrastructure in a structural model of
economic growth. Regional Science and Urban Economics 25, pp. 131-151.
Holtz-Eakin, D., M. Lovely and M. Tosun, 2004, Generational Conflict, Fiscal Policy and
Economic Growth. Journal of Macroeconomics 26, 1-23.
Hubbard, Glenn R. and Kenneth L. Judd. 1987, Social Security and Individual Welfare:
Precautionary Saving, Liquidity Constraints, and the Payroll Tax. American Economic
Review, September, 77(4), pp.660-46.
Hulten, C., 1996, Infrastructure capital and economic growth: how well you use it may be
more important than how much you have. NBER Working Paper No. 5847.
Hulten, C. and R. M. Schwab, 1991, Public capital formation and the growth of regional
manufacturing industries. National Tax Journal, 121-134.
Hurd, Michael D, 1989, Mortality Risk and Bequests. Econometrica, July, 57(4), pp.779813.
Kanczuk, F., 2004, Real interest rates and Chileian business cycles. Review of Economic
Dynamics 7, 436-455.
King, Robert, Charles Plosser, and Sergio Rebelo, 1988, "Production, Growth, and
Business Cycles I: Basic Neo-classical Model" Journal of Monetary Economics 21, 195232.
Lucas Jr., R. E., 1990, Supply-side economics: an analytical review. Oxford Economic
Papers 42, pp. 293-316.
Lynde, C. and J. Richmond, 1993, Public capital and total factor productivity,
International Economic Review 34, 401-414.
Rebelo, S. and C.A. Vegh, 1995, Real effects of exchange rate-based stabilization: an
analysis of competing theories. NBER Working Paper No. 5197, National Bureau of
Economic Research.
15
Rioja, Felix, 1999, Productiveness and welfare implications of public infrastructure: a
dynamic two-sector general equilibrium analysis. Journal of Development Economics 58,
387-404.
Rioja, Felix, 2003, “Filling Potholes: Macroeconomic Effects of Maintenance vs. New
Investments in Public Infrastructure", Journal of Public Economics, 87 (9-10), September
2003, pp. 2281-2304.
Sachs, Jeffrey, 1989, Social Conflict and Populist Policies in Latin America. NBER
Working Paper no. 2897. Cambridge, Mass.
Schmitt-Grohe, S. and M Uribe, 2003. Closing small open economy models Journal of
International Economics, 61.
Turnovsky, S., 1999, Productive Government Expenditure in a Stochastically Growing
Economy, Macroeconomic Dynamics 3, 544-570.
_____________, 1997, Public and private capital in an endogenously growing open
economy, in B.S. Jensen and K. Wong (eds.), Dynamics, Economic Growth, and
International Trade, Ann Arbor: The University of Michigan Press.
World Bank, 2003, Chile Stability for Growth and Poverty Reduction.
16