Download Review 1

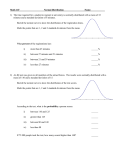
Review 2
2002.11.7
Chapters 3, 4
Measures of Location, Dispersion, Exploratory Data Analysis,
Measure of Relative Location, Weighted and Grouped Mean and
Variance, Association between Two Variables
Example:
The flashlight batteries produced by one of the manufacturers are known
to have an average life of 60 hours with a standard deviation of 4 hours.
(a) At least what percentage of batteries will have a life of 54 to 66 hours?
(b) At least what percentage of the batteries will have a life of 52 to 68
hours?
(c) Determine an interval for the batteries’ lives that will be true for at
least 80% of the batteries.
[solution:]
Denote
x  60, s  4
(a)
[54,66]  60  6  x  1.5s
Thus, by Chebyshev’s theorem, within 1.5 standard deviation, there is at
least
1 

 100%  55.55%
1 
2 
 1.5 
of batteries.
(b)
[52,68]  60  8  x  2s
Thus, by Chebyshev’s theorem, within 1.5 standard deviation, there is at
least
1
1 

1  2   100%  75%
 2 
of batteries.
(c)
1 
1

1  2   100%  80%  1  2  0.8  k  5
k
 k 
Thus, within
Therefore,
5 standard deviation, there is at least 80% of batteries.
x  5s  60  5  4  60  8.94  51.06,68.94 .
Chapter 5
Basic Relationships of Probability, Conditional Probability and
Bayes’ Theorem
Example:
The following are the data on the gender and marital status of 200
customers of a company.
Single
Married
Male
20
100
Female
30
50
(a) What is the probability of finding a single female customer?
(b) What is the probability of finding a married male customer?
(c) If a customer is female, what is the probability that she is single?
(d) What percentage of customers is male?
(e) If a customer is male, what is the probability that he is married?
(f) Are gender and martial status mutually exclusive? Explain.
(g) Is martial status independent of gender? Explain.
[solution:]
A1: the customers are single
A2: the customers are married
2
B1: the customers are male.
B2: the customers are female.
(a)
P A1  B2  
30
 0.15
200
P A2  B1  
100
 0.5
200
(b)
(c)
P A1 | B2  
P A1  B2 
PB2  .
Since
PB2   P A1  B2   P A2  B2  
30
50
80


,
200 200 200
30
P A1  B2  200 30
P A1 | B2  


 0.375
.
80
PB2 
80
200
(d)
PB1   P A1  B1   P A2  B1  
20 100 120


 0.6
200 200 200
(e)
100
P A2  B1  200 100 5
P A2 | B1  



120 120 6 .
PB1 
200
(f)
Gender and martial status are not mutually exclusive since
P A1  B1   0
3
(f)
Gender and martial status are not independent since
P A1 | B2  
30
50

 P A1  .
80 200
Example:
In a recent survey in a Statistics class, it was determined that only 60% of
the students attend class on Thursday. From past data it was noted that
98% of those who went to class on Thursday pass the course, while only
20% of those who did not go to class on Thursday passed the course.
(a) What percentage of students is expected to pass the course?
(b) Given that a student passes the course, what is the probability that
he/she attended classes on Thursday.
[solution:]
A1: the students attend class on Thursday
A2: the students do not attend class on Thursday
 A1  A2  
B1: the students pass the course
B2: the students do not pass the course
P A1   0.6, P A2   1  P A1   0.4, PB1 | A1   0.98, PB1 | A2   0.2
(a)
P B1   P B1  A1   P B1  A2 
 P  A1 P B1 | A1   P  A2 P B1 | A2 
 0.6  0.98  0.4  0.2
 0.668
(b)
By Bayes’ theorem,
4
P( A1 | B1 ) 
P A1  B1 
P( A1) P( B1 | A1)

PB1 
P( A1) P( B1 | A1)  P( A2) P( B1 | A2)
0.6  0.98
0.6  0.98  0.4  0.2
 0.854

Chapter 6
1. Random Variables, Discrete Probability Function and Continuous
Probability Density
Example:
The probability distribution function for a discrete random variable X is
f ( x )  2k , x  1
3k , x  3
4k , x  5
0, otherwise
where k is some constant. Please find
(a) k. (b) P( X  2)
[solution:]
(a)
 f ( x)  f (1)  f (3)  f (5)  2k  3k  4k  9k  1
x
 k 
(b)
1
.
9
P( X  2)  P( X  3 or X  5)  P( X  3)  P( X  5)
1 7
 f (3)  f (5)  3k  4k  7k  7  
9 9
5
.