Download Ch - Garnet Valley School District

Name _______________________________________ Date __________________ Class __________________
Midterm Review Sheet #1
Select the best answer. Grid your answer into the box to the left.
Write
answers
to the
questions
below.
1.A vacation home in Orlando, Florida, rents
for $105 per day. The function
f(x)  105x gives the cost of renting the
home for x days. What is the domain of
this function?
F x0
1.
G {0, 1, 2, 3, ...}
2.
H {0, 105, 210, 315, ...}
J all real numbers
3.
4.
5.
6.
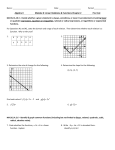
4. Find the slope of this line.
2. A parking meter gives 30 minutes for
each quarter and 6 minutes for each
nickel. The equation 30x  6y  60
describes the number of quarters x and
nickels y that you need to park for
60 minutes. What does the x-intercept
represent?
A You need 2 quarters and no nickels
to park for 60 minutes.
B You need 10 nickels and no
quarters to park for 60 minutes.
C You need 6 nickels and no quarters
to park for 60 minutes.
D You need 30 quarters and no
nickels to park for 60 minutes.
3.This table shows the U.S. federal
minimum hourly wage in different years.
During which time interval did the wage
increase at the greatest rate?
Year
1979 1980 1981 1990 1991
Wage
($)
2.90
3.10
3.35
3.80
A 
5
2
C
2
5
B 
2
5
D
5
2
5. Find the slope of the line that contains
the points (1, 1) and (2, 8).
F 5
H 
7
3
G 3
J 
1
3
6.Which equation describes the line with a
slope of 5 and y-intercept of 3?
F y  3x  5
H y  5x  3
G y  3x  5
J y  5x  3
4.25
F 1979 to 1980
H 1981 to 1990
G 1980 to 1981
J 1990 to 1991
Original content Copyright © by Holt McDougal. Additions and changes to the original content are the responsibility of the instructor.
Holt McDougal Algebra 1
Name _______________________________________ Date __________________ Class __________________
10.Here are four linear equations.
7.What is the slope and y-intercept of the
graph?
I 4x  3y  15
III y  1 
II 3x  4y  8
4
3
(x – 6) IV y  x  5
3
4
Which pair of lines are parallel?
Write
answers
to the
questions
below.
8.
12.
13.
G I and III
J III and IV
A y  2x  4
9.
11.
H II and IV
11. Which equation describes a line that
passes through (6, 8) and is
perpendicular to the line described
by y  2x  4?
7.
10.
F I and II
1
, y-intercept  2
4
1
B slope   , y-intercept  3
4
C slope  4, y-intercept  4
D slope  4, y-intercept  4
A slope  
B y
1
x5
2
C y
1
x  11
2
D y  2x  20
12. Graph f(x)  3x  4 and g(x)  3x  4.
Which describes the transformation(s)
from the graph of f(x) to the graph of
g(x)?
8. Which equation describes the line with a
slope of 2 that contains the point (4, 3)?
F. y  4  2(x  3) H. y  3  2(x – 4)
G. 2(y – 3)  x  4 J. 2(y 4)  x  3
9. The table shows the age of several
people and how many hours a day they
spend playing computer and/or video
games.
Age
(yrs)
15
63
33
22
15
F a reflection across the y-axis
Playing
(hrs/day)
5
0
2
8
0
G a reflection across the y-axis and a
translation 4 units up
Which equation could represent a line of
best fit for this data?
A y ≈ 53x – 7.9
B y ≈ –7.9x + 53
C y ≈ 5.3x – 0.079
D y ≈ –0.079x + 5.3
H a rotation (less steep) about (0, 4)
J a translation up 6 units
13.Which ordered pair is a solution of
 x  y  3
?

2x  y  0
A (3, 0)
C (0, 0)
B (1, 2)
D (1, 4)
Original content Copyright © by Holt McDougal. Additions and changes to the original content are the responsibility of the instructor.
Holt McDougal Algebra 1
Name _______________________________________ Date __________________ Class __________________
14. The graph of a system of linear equations
is shown below. What is the solution of
the system?
Write
answers
to the
questions
below.
C inconsistent
D independent
19. Which linear equation best fits this
data set?
15.
16.
17.
18.
F (0, 3)
H (2, 4)
19.
G (0, 6)
J (6, 0)
21.
A consistent
B dependent
14.
20.
18.Which term describes a system with no
solution?
y  x  3
.
15. Solve by substitution: 
2x  y  9
A (1.5, 4.5)
B (2, 5)
x
1
4
6
8
11
y
2
3
6
5
8
3
5
x
5
4
2
5
G y  x
3
2
F y
H yx1
J y
4
1
x
3
2
20. Which of these is the domain and range
2
for the parent function of 3  x  1  2 ?
A Domain: x  0 Range: y  0
C (3, 6)
B Domain: all real numbers Range:
D (6, 9)
3x  2y  1
.
16. Solve by elimination: 
 x  2y  11
F (5, 8)
H (3, 4)
 5 17 
G  ,- 
2 4 
7

J  4,  
2

y 0
C Domain: all real numbers Range:
y 0
D Domain: x  0 Range: y  0
21. Which is the type of correlation shown?
17. Sam needs to make a long-distance call
from a pay phone. With his prepaid phone
card, he will be charged $1.00 to connect and
$0.50 per minute. If he places a collect call
with the operator he will be charged $3.00 to
connect and $0.25 per minute. In how many
minutes will the phone card and the collect
call cost the same?
A 5 min
B 5
1
min
3
F no correlation H positive
G negative
J zero
C 8 min
D 16 min
Original content Copyright © by Holt McDougal. Additions and changes to the original content are the responsibility of the instructor.
Holt McDougal Algebra 1
Name _______________________________________ Date __________________ Class __________________
22. Which is the best estimate of the
correlation coefficient?
27. What is the minimum or maximum of
g  x   9x 2  6x  1?
Write
answers
to the
questions
below.
1

1

F minimum:  , 0  H minimum: (3, 0)
3 
G maximum:  , 0  J maximum: (3, 0)
3 
22.
28. What are the zeros of the trinomial
2x 2  3x  1?
23.
24.
25.
26.
27.
28.
29.
30.
31.
F -0.92
H 0.92
G 0
J 1
A 1,1
23. Using f ( x )  x 2 , what is the transformation
that yields f ( x )  3  x  2   3 ?
2
F vertical stretch of 2, shift 3 units left
and 3 units down
G shift 12 units left and 3 units down
C 1,  1
2
2
B 2, 1
D 1, 2
29. What is a quadratic function in standard
form having zeros of 3 and


1
H vertical stretch of 2, shift 2 units right
and 3 units down
F f ( x )   x  3  x  
2
J vertical stretch of 3, shift 2 units left
and 3 units down
G f ( x )  2x 2  5 x  3
24. What is the simplified version of
i 18 225 ?
A 15i
C 15i
B 15
D 15


1
?
2

1
H f ( x )   x  3  x  
2

J f ( x )  2x  5 x  3
2
30.For the discriminant
 5 
2
 4  4  2, What
is the number of solutions and their
type(s)?
25. Use the quadratic formula to solve
3x 2  10x  3 = 0.
F x
1
3
H x
B 1 real solution
1
,3
3
J x  3, 
G x  3 i
A 2 imaginary solutions
C 1 imaginary solution
1
3
26. Consider h  x   3x  6x  2 .What is its
D 2 real solutions



31.Simplify i 10  4 i 10  4 .
2
vertex and y-intercept?
A vertex: (1, 1), y-intercept: (0, 2)
A 10i 2  16
C  10  4
B 6
D 26
B vertex: (2, 2), y-intercept: (0, 2)
C vertex: (1, 1), y-intercept: (0, 2)
D vertex: (2, 1), y-intercept: (0, 2)
Original content Copyright © by Holt McDougal. Additions and changes to the original content are the responsibility of the instructor.
Holt McDougal Algebra 1
Name _______________________________________ Date __________________ Class __________________
32. Simplify 3  4i .
1  4i
Write
answers
to the
questions
below.
32.
F
13  16i
17
G 13
17
H 13  8i
J 19  8i
17
33. Write a quadratic equation that fits the points (2, 27), (4, 61), and (7, 142).
33.
A x2  10x  3
C 2x2  4x  13
34.
B x2  11x  1
D 2x2  5x  9
34. Carmen is standing on the ground. She tries to throw a tennis ball over her house, but it hits
the roof on the way down at a height of 33 feet. The quadratic equation that models the
path of the ball is b(t)  16t2  56t. How long did it take for the ball to hit the roof after it left
Carmen’s hand?
F 0.75 seconds
H 2.25 seconds
G 1.5 seconds
J 2.75 seconds
Original content Copyright © by Holt McDougal. Additions and changes to the original content are the responsibility of the instructor.
Holt McDougal Algebra 1