* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 3.3 Relating Parallel and Perpendicular Lines a Theorem 3-9:
Survey
Document related concepts
Duality (projective geometry) wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Multilateration wikipedia , lookup
Noether's theorem wikipedia , lookup
Technical drawing wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Perspective (graphical) wikipedia , lookup
Four color theorem wikipedia , lookup
Perceived visual angle wikipedia , lookup
Line (geometry) wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
Trigonometric functions wikipedia , lookup
Integer triangle wikipedia , lookup
History of trigonometry wikipedia , lookup
Transcript
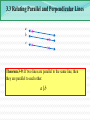
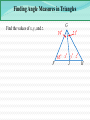
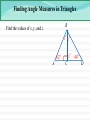
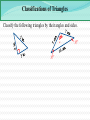
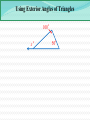
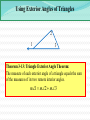
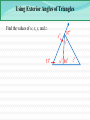
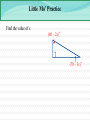
3.3 Relating Parallel and Perpendicular Lines a b c Theorem 3-9: If two lines are parallel to the same line, then they are parallel to each other. a || b Relating Parallel and Perpendicular Lines t m n Theorem 3-10: In a plane, if two lines are perpendicular to the same line, then they are parallel to each other. m || n Relating Parallel and Perpendicular Lines t m 1 2 n Given : m t, n t Prove : m || n Statements Reasons 1. m t, n t 1. 2. 1 and 2 are right angles 2. 3. 1 2 3. m || n 4. 4. Relating Parallel and Perpendicular Lines n l m Theorem 3-11: In a plane, if a line is perpendicular to one of two parallel lines, then it is also perpendicular to the other. nm Relating Parallel and Perpendicular Lines n 1 l 2 Given : n l, and l || m Prove : n m Statements Reasons 1. n l, and l || m 1. 2. 1 is a right 2. 3. 3. Corresp. ‘s post. 4. n m 4. m 3.4 - Finding Angle Measures in Triangles C 50° 35° A B Theorem 3-12: Triangle Angle-Sum Theorem: The sum of the measures of the angles of a triangle is 180. mA mB mC 180 Finding Angle Measures in Triangles Finding Angle Measures in Triangles G Find the values of x, y, and z. 39° 21° 65° x° y° z° F J H Finding Angle Measures in Triangles B Find the values of x, y, and z. x°y° z° 49° 62° A C D Classifications of Triangles Equiangular All 's are Acute All 's acute Equilateral All sides Right One right Obtuse One obtuse Isosceles At least 2 sides Scalene No sides Classifications of Triangles Classify the following triangles by their angles and sides. 37° 37° Using Exterior Angles of Triangles Exterior Angle of a Polygon: An angle formed by a side and an extension of an adjacent side. Exterior Angle 2 1 3 Remote Interior Angles Remote Interior Angles: The two nonadjacent interior angles corresponding to each exterior angle of a triangle. Using Exterior Angles of Triangles 100° x° 50° Using Exterior Angles of Triangles 2 1 3 Theorem 3-13: Triangle Exterior Angle Theorem: The measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles. m1 m2 m3 Using Exterior Angles of Triangles Find the values of w, x, y, and z. x° 97° y° 53° w°86° z° Little Mo’ Practice Find the value of x. (80 – 2x)° (70 – 3x)° Homework #14 3.3 Proof Worksheet Pg 150 #1-6, 18-20, 23-26 3.1-3.4 QUIZ MONDAY!!!!!!