Download Review Janice 2 1. Intelligence Quotient (IQ) in a certain population

Review Janice 2
1.
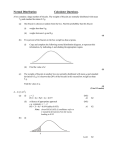
Intelligence Quotient (IQ) in a certain population is normally distributed with a mean of 100 and
a standard deviation of 15.
(a)
What percentage of the population has an IQ between 90 and 125?
(2)
(b)
If two persons are chosen at random from the population, what is the probability that both
have an IQ greater than 125?
(3)
(c)
The mean IQ of a random group of 25 persons suffering from a certain brain disorder was
found to be 95.2. Is this sufficient evidence, at the 0.05 level of significance, that people
suffering from the disorder have, on average, a lower IQ than the entire population? State
your null hypothesis and your alternative hypothesis, and explain your reasoning.
(4)
(Total 9 marks)
2.
In a country called Tallopia, the height of adults is normally distributed with a mean of
187.5 cm and a standard deviation of 9.5 cm.
(a)
What percentage of adults in Tallopia have a height greater than 197 cm?
(3)
(b)
A standard doorway in Tallopia is designed so that 99% of adults have a space of at least
17 cm over their heads when going through a doorway. Find the height of a standard
doorway in Tallopia. Give your answer to the nearest cm.
(4)
(Total 7 marks)
1
3.
The heights of a group of students are normally distributed with a mean of 160 cm and a
standard deviation of 20 cm.
(a)
A student is chosen at random. Find the probability that the student’s height is greater
than 180 cm.
(b)
In this group of students, 11.9 have heights less than d cm. Find the value of d.
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
..............................................................................................................................................
(Total 6 marks)
2
4.
The following diagram represents the lengths, in cm, of 80 plants grown in a laboratory.
20
15
frequency
10
5
0
(a)
0
10
20
30
40
50
60
length (cm)
70
80
90
100
How many plants have lengths in cm between
(i)
50 and 60?
(ii)
70 and 90?
(2)
(b)
Calculate estimates for the mean and the standard deviation of the lengths of the plants.
(4)
(c)
Explain what feature of the diagram suggests that the median is different from the mean.
(1)
(d)
The following is an extract from the cumulative frequency table.
length in cm
cumulative
less than
frequency
.
.
50
22
60
32
70
48
80
62
.
.
Use the information in the table to estimate the median. Give your answer to two
significant figures.
(3)
(Total 10 marks)
3
5.
A box contains a large number of biscuits. The weights of biscuits are normally distributed with
mean 7 g and standard deviation 0.5 g.
(a)
One biscuit is chosen at random from the box. Find the probability that this biscuit
(i)
weighs less than 8 g;
(ii)
weighs between 6 g and 8 g.
(4)
(b)
Five percent of the biscuits in the box weigh less than d grams.
(i)
Copy and complete the following normal distribution diagram, to represent this
information, by indicating d, and shading the appropriate region.
(ii)
Find the value of d.
(5)
(c)
The weights of biscuits in another box are normally distributed with mean  and standard
deviation 0.5 g. It is known that 20 of the biscuits in this second box weigh less than 5
g.
Find the value of .
(4)
(Total 13 marks)
4
1.
(a)
Let X be the random variable for the IQ.
X ~ N(100, 225)
P(90 < X < 125) = P(–0.67 < Z < 1.67)
= 0.701
70.1 percent of the population (accept 70 percent).
(M1)
(A1)
OR
(b)
(c)
P(90 < X < 125) = 70.1%
(G2)
2
P( X ≥ 125) = 0.0475 (or 0.0478)
P(both persons having IQ ≥ 125) = (0.0475)2 (or (0.0478)2)
= 0.00226 (or 0.00228)
(M1)
(M1)
(A1)
3
Null hypothesis (H0): mean IQ of people with disorder is 100
Alternative hypothesis (H1): mean IQ of people with disorder
is less than 100






95.2  100  


P( X < 95.2) = P  Z 
= P(Z < –1.6) = 1 – 0.9452


15



25  


= 0.0548
The probability that the sample mean is 95.2 and the null hypothesis
true is 0.0548 > 0.05. Hence the evidence is not sufficient.
(M1)
(M1)
(A1)
(R1)
4
[9]
2.
Note: Where accuracy is not specified, accept answers with greater than 3 sf
accuracy, provided they are correct as far as 3 sf
(a)
z=
197 – 187.5
= 1.00
9 .5
P (Z > 1) = 1 – (1) = 1 – 0.8413 = 0.1587
= 0.159 (3 sf)
= 15.9%
OR
P (H > 197) = 0.159
= 15.9%
(b)
(M1)
(A1)
(A1)
(G2)
(A1)
Finding the 99th percentile
(a) = 0.99 => a = 2.327 (accept 2.33)
=> 99% of heights under 187.5 + 2.327(9.5) = 209.6065
= 210 (3 sf)
OR
99% of heights under 209.6 = 210 cm (3 sf)
(A1)
(M1)
(A1)
Height of standard doorway = 210 + 17 = 227 cm
(A1)
3
(G3)
4
[7]
5
3.
(a)
z
180  160
1
20
(A1)
 (1) = 0.8413
(A1)
P(height > 180) = 1  0.8413
= 0.159
(b)
A1
z = 1.1800
N3
(A1)
Setting up equation 1.18 =
d 160
20
(M1)
d = 136
A1
N3
[6]
4.
(a)
(i)
10
(A1)
(ii)
14 + 10 = 24
(A1)
2
(b)





(A1)





xi
fi
15
25
35
45
55
65
75
85
95
1
5
7
9
10
16
14
10
8





(A1)





80
(AG)
Note: Award (A0) for using the mid-interval values of 14.5,
24.5 etc.
(c)
(i)
 = 63
(A1)
(ii)
 = 20.5 (3 sf)
(A1)
4
(A1)
1
Assymetric diagram/distribution
6
(d)
60
cumulative
frequency
40.5
(A1)
{
(A1)
points and
curve
20
50
70
60
65
length (cm) (A1)
80
3
OR Median = 65
(A3)
Note: This answer assumes appropriate use of a calculator with
correct arguments.
OR Linear interpolation on the table:
 48  40.5 
 40.5  32 

  60  
 × 70 = 65 (2sf)
 48  32 
 48  32 
3
(M1)
(A1)(A1)
3
[10]
5.
X ~ N (7, 0.52)
(a)
(i)
(ii)
z=2
P(X < 8) = P(Z < 2) = 0.977
(M1)
A1
evidence of appropriate approach
eg symmetry, z = 2
P(6 < X < 8) = 0.954 (tables 0.955)
Note: Award M1A1(AP) if candidates refer to
2 standard deviations from the mean,
leading to 0.95.
(M1)
A1
N2
N2
7
(b)
(i)
d
A1A1
N2
Note: Award A1 for d to the left of the mean, A1
for area to the left of d shaded.
(ii)
z =  1.645
(A1)
d 7
 1.645
0 .5
(M1)
d = 6.18
(c)
Y ~ N(, 0.52)
P(Y < 5) = 0.2
z =  0.84162...
5
  0.8416
0 .5
 = 5.42
A1
N3
(M1)
A1
(M1)
A1
N3
[13]
8