Download Hypothesis Testing

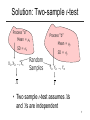
Business Statistics
Lecture 8: More Hypothesis
Testing
1
Goals for this Lecture
• Review of t-tests
• Additional hypothesis tests
• Two-sample tests
• Paired tests
2
The Basic Idea of Hypothesis Testing
• Start with a theory or hypothesis
• For example,
m = 814.3
• Collect some data
• Ask: How unusual is it to see this data if
the null hypothesis is true?
• If it’s unusual, reject the null hypothesis
• If not, fail to reject the null
• Remember, determine the hypothesis to
be tested before looking before looking
at the data
3
It All Ties Back to the Empirical Rule
68%
95%
-4
-3
-2
-1
0
Z
1
2
3
4
• If we hypothesize that the data come from a N(0,1)
distribution, how unusual an observation must we see to
reject our hypothesis?
It depends on the alternative hypothesis…
4
For Example, a Two-sided Test
Null: The mean is equal to zero (H0: m = 0)
Alternative: The mean is not equal to zero (Ha: m ≠ 0)
If the rejection criterion is p-value < 0.05, we reject if our
observation is greater than 1.96 or less than -1.96:
68%
95%
-4
-3
-2
-1
0
Z
1
2
3
4
5
In JMP
• JMP computes the probability of seeing
data as extreme or more extreme under
various alternate hypotheses
• You have to choose the appropriate p-value
• Then compare the JMP p-value to 0.05
• Smaller: reject the null
• Larger: fail to reject the null
• Output is in terms of rescaled “t-scores”
• Using t distribution comes from using s to
estimate s
6
Conducting the Test in JMP
• With one continuous variable, Analyze >
Distribution > red triangle > Test Mean
• Type in the mean to be tested (“Specify
Hypothesized Mean”)
• If population (“true”) standard deviation
known, enter it
•
This will be a z-test
• If you leave it blank, JMP does a t-test
• It uses s to estimate s
7
Back to the Paint Case
(primer.jmp)
• A More Complicated Question:
• Suppose we are less interested in the
value of 1.2 and more interested in
whether processes “a” and “b” have
the same mean
• Null hypothesis
•
Means are the same: ma- mb = 0
• Alternative hypothesis
• Means are different: ma- mb  0
8
Solution: Two-sample t-test
Process “a”
Mean = mx
Process “b”
Mean = my
SD = sx
X1, X2, …, Xn
X
Random
Samples
SD = sy
Y1, Y2, …, Ym
Y
• Two sample t-test assumes Xs
and Ys are independent
9
Results of Two Sample t-test
• What do you think the test statistic is?
• How should we rescale the test statistic?
• What does the p-value represent?
10
Two-sample t-test
• Null Hypothesis: mx- my = 0
• Test Statistic: X  Y
• Fact: since X and Y are independent:
Var ( X  Y )  Var ( X )  Var ( Y )

• So
SE ( X  Y ) 
s
2
x

n
s
2
x
n

s y2
m
s y2
m
11
Rescaled Test Statistic
• Test statistic: X  Y
• Estimated standard error:
• Rescaled test statistic:
2
s y2
sx

nx n y
X Y   0

t
2
s y2
sx

nx n y
12
Remember: Rescaling
• For some test statistic T where m and s
are not known, compute
t
where
•
T m
*
sT
m * is the hypothesized true value
• sT is the sample standard error of the
statistic T
13
One-sample and Two-sample Tests
• In a one-sample test of, choose m*
• Then T = X , so the test statistic is
t
T  m*
s.d .(T )

X  m*
s.e.( X )
• In a two-sample test, you’re often
testing whether the means are equal
• T = X  Y , and the test statistic is
T m
(X Y )  0
(X Y )
t


s.d .(T ) s.e.( X  Y ) s.e.( X  Y )
*
14
Equal Variances?
• We must estimate sx and sy
• If sx = sy then we can get a better
estimate
• Remember: Sample variance for a
single sample:
Sample mean
s
2
n
1
2

(
x

x
)

j
j 1
n 1
Average squared deviation
from the mean
Deviations from
sample mean
15
Different Means But Similar SD
• Remember, SD is
calculated using
differences from
the mean
• Each group can
have very different
mean but standard
deviations can be
similar
6
5
4
3
2
1
0
-1
-2
-3
16
More Bang for the Buck
• Pooled estimate of sample variance:
Sample mean
for process a
s
2
p


n
j 1
Sample mean
for process b
( x j  x )   j 1 ( y j  y )
2
m
2
(n  1)  (m  1)
Average squared deviation
from different means
Used two degrees of
freedom, n+m-2 left over
• Pooled estimate buys you more df
2
2
s
s
• Weighted average of x and y
17
Conducting the Test in JMP
• Need two variables: one continuous and one
categorical (denoting group)
• Then: Analyze > Fit Y by X (continuous
variable is the Y and categorical the X) > red
triangle > Means/Anova/Pooled t
• See the “t Test” part of the output
18
Case: Taste Testing Teas
• Small taste test of teas (taste.jmp)
• 16 panelists in a focus group
• Each tasted two formulations of a
prepackaged iced tea
• Rated them on a scale of 1 (excellent) to 7
(really bad)
• Company wants to know if there is a
difference in ratings between the two
formulations
19
An Initial Evaluation
• Two-sample t-test on taste.jmp:
• Is there a
significant
difference?
20
Taste Case: Any Difference?
• Unless SD’s vastly different (factor of 2), the
equal variance assumption no big deal
21
Independence Assumption
Very Important
• Independence assumption for two
sample t-test is violated
• Good news: there is an alternate test
that can do even better
• Paired t-test assumes two observations
taken for each unit in the sample
• Observations on the same unit likely to be
more similar than obs’ns on different units
• Here same person tasted each formulation
22
Paired t-test Looks at Differences
x1-y1=d1
x2-y2=d2
•
.
•
•
xn-yn=dn
• Calculate differences for
each observation
• Calculate sample mean and
SD of differences
• Do a one sample t-test for
differences:
• H0: mean difference is zero
• Ha: mean difference is not 0
23
Paired t-test in JMP
• Use Analyze >
Matched Pairs
• Two variables,
paired by row:
24
Results: Paired t-test in JMP
Mean Difference is
same as two
sample test
SE is
smaller –
why??
25
Why Pairing Helps
• Heuristic:
• When xj and yj “vary together” then yj will
be big when xj is big
• Since xj & yj tend to be close together, xj-yj
is smaller than when X and Y independent
• Math:
• When
X and Y are not independent then
Var ( X  Y )  Var ( X )  Var (Y )  2Cov( X , Y )
• Cov or “covariance” measures linear
dependence between two variables
26
It Helps in this Case Because…
• People first have a like or dislike for tea
• Their ratings of the formulations are relative to
this overall opinion of tea
• Taking the difference removes the “person
effect”
7
Tend to
like tea
6
Tend to
dislike tea
Taste 1
5
4
3
2
1
0
0
1
2
3
4
Taste 2
5
6
7
8
27
Independence vs. Dependence
4
3
3
2
2
1
1
0
0
-1
-1
-2
-2
-3
-3
-3
-2
-1
0
X
1
2
3
-3
-2
-1
0
1
2
3
X
• xj-yj is horizontal distance to the y=x line
• xj-yj is smaller (typically) in the right hand plot
28
Case: Sales Force Comparison
• Newly merged pharmaceutical company
(PharmSal.jmp)
• Two sales forces (“BW” & “GL”), one from
each of the merged companies
• 20 sales districts are the same
•
Sales reps divided into these districts
• Sell essentially the same drugs
• Management wants to know if one sales
force outperforms the other
29
Sales by Division
550
500
450
Sales
400
350
300
250
200
150
100
BW
GL
Division
Quantiles
Level
BW
GL
Minimum
112
119
10%
25%
Median
75%
90%
151.1
151.6
215.25
197.75
291
313.5
385.5
409.75
428.5
460.6
Maximum
525
547
30
Two-Sample t-test Results
550
• Under the independence
assumption, we conclude
that there is no difference
in the means
500
450
Sales
400
350
300
250
200
150
100
BW
GL
• But are they
independent?
Division
31
The Sales Forces Are Dependent
• Dependence occurs by sales district:
32
Paired t-test Comparison
• Which
sales force
is doing
better?
33
More Complicated Tests
• There are even more complicated tests
you can do
• E.G., test for equal variance
• You’re never going to remember all the
steps for each test anyway
• Let the computer do it for you
34
Terminology
• One-sided vs. two-sided
• Comes from the statement of the
alternative hypothesis
• Are you calculating the p-value using one
tail or two?
• One-sample vs. two-sample
• Comes from the type of data and the
question you are answering
• Are you testing a mean or a difference
between means?
35
Which Test?
• How many populations are sampled?
• One: one-sample test
• Two: read on
• Are observations in first sample independent
of observations in second sample?
• Yes: two-sample t-test
• No: paired t-test
• Big Clue:
• Paired t-test needs two observations from each
unit
•
•
Unequal sample sizes  2 sample test
Equal sample sizes you have to decide
36
Hypothesis Tests in the Computer Age
• Know the null and alternative
hypotheses
• Have some idea of what test statistics
you would look at
• Let the computer figure out how to
rescale them
• Let the computer figure out the p-value
• p-values are always interpreted the
same way
37
What we have learned so far…
• Descriptive Statistics
• Probability
• Inference for a population mean
• Confidence intervals
• Hypothesis testing
• One-sample test of the mean
• Two-sample tests
• Paired tests
38