* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Basic Filter Theory Review
Nominal impedance wikipedia , lookup
Loading coil wikipedia , lookup
Loudspeaker enclosure wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Transmission line loudspeaker wikipedia , lookup
Spectrum analyzer wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Opto-isolator wikipedia , lookup
Chirp compression wikipedia , lookup
Chirp spectrum wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Zobel network wikipedia , lookup
Ringing artifacts wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Mechanical filter wikipedia , lookup
Audio crossover wikipedia , lookup
Basic Filter Theory Review
• Loading tends to
make filter’s
response very
droopy, which is
quite undesirable
• To prevent such
loading, filter
sections may be
isolated using
high-inputimpedance buffers
• ‘A’ is closed-loop
gain of op amp
H(jf) dB = 20 log [A/{sqrt(1+(f/fc)2}] <-tan-1 (f/fC)
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
Higher-Order LP Filters
• Higher-order filters may be realized by cascading basic RC sections
• Higher the order of filter, more closely its response resembles that
of ideal brick wall filter
Frequency
response curves
for LP filters
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
Second-Order LP Filters
•
•
•
•
•
•
Second-order LP filter may be designed using two cascaded RC sections or by using an LC
section
LC filter is not restricted to one single response shape
Corner frequency of LC filter is given by
fc = 1/[2πSqrt(LC)]
A given LC product can be achieved using infinitely many different inductor and capacitor
combinations giving much more flexibility in terms of response shape
Using high C to L ratio results in low damping coefficient (α) and peaking in response curve
Using low C to L ratio results in higher α and smoother response curve
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
•
•
•
•
•
•
•
•
Second-Order LP LC Filters
α = 1.414: response is as flat as possible in
passband and is called critical damping
Lower α result in peaking near corner and more
rapid attenuation in transition region ultimate
rolloff is -40 dB/decade for second-order filter
Filters with flat response in passband: Butterworth
filters
Filters with peaked response in passband:
Chebyshev filters
Filters with α < 1.414: underdamped
Filters with α > 1.414: overdamped
Filters with α = 1.414: critically damped
α also affects location of fc
– Critically damped filters: no effect
– Underdamped filters: increase in fc
– Overdamped filters: decrease in fc
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
Effect of Damping
Coefficient on secondorder LP LC filter
Second-Order LP LC Filters
•
•
•
•
Frequency scaling factors Kf indicated relative increase or decrease from fc of
an equivalent filter with α = 1.414
fc of a second-order Butterworth active filter fc = 1/[2πSqrt(C1C2R1R2)]
If α is changed, new fc would be given by fc = Kf/[2πSqrt(C1C2R1R2)]
Bessel filter: provides nearly linear phase shift as function of frequency; has
droopy passband response with gradual rolloff and very low overshoot for
transient inputs (no ringing)
– α = 1.732, Kf = 0.785
•
Butterworth filter: allowing flattest possible passband; most popular filter
– α = 1.414, Kf = 1
•
Chebyshev filters: allow peaking in passband, with more rapid transitionregion attenuation; higher the peaking, more nonlinear the phase response
becomes, and more rapid the transition-region attenuation becomes; these
filters tend to overshoot and ring in response to transients
– 1-dB Chebyshev filters α = 1.045, Kf = 1.159
– 2-dB Chebyshev filters α = 0.895, Kf = 1.174
– 3-dB Chebyshev filters α = 0.767, Kf = 1.189
Second-Order LP LC Filters
Effects of damping
on phase response
of second-order LP
LC filters
Second-order filters are very frequently encountered
in many applications
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
Second-Order LP HP Filters
• Decibel gain magnitudes for second-order LP
filters in terms of damping coefficient
– H(jf) dB = 20 log [A/{Sqrt(1+(α2-2)(f/fc)2+(f/fc)4}]
– For nth order Butterworth response (α = 1.414)
H(jf) dB = 20 log [A/{Sqrt(1+(f/fc)2n}]
• Second-order HP filters
– H(jf) dB = 20 log [A/{Sqrt(1+(α2-2)(fc/f)2+(fc/f)4}]
– For nth order Butterworth response (α = 1.414)
H(jf) dB = 20 log [A/{Sqrt(1+(fc/f)2n}]
Active LP and HP Filters
• It is not possible to produce passive RC filter with
α = 1.414
• Using passive filter techniques, one must resort
to inductor-capacitor designs in such cases
• At low frequencies, inductors required to produce
many response shapes tend to be excessively
large, heavy, and expensive
• Inductors generally tend to pick up
electromagnetic interference quite readily
• Hence, active filters are highly popular
Sallen-Key LP and HP Filters
• Sallen-Key active LP & HP filters are extremely popular
– Unity Gain Sallen-Key VCVS
– Equal-Component Sallen-Key VCVS
• Both types use op amp in noninverting configuration as
a VCVS
• Unity Gain Sallen-Key VCVS
Unity Gain SallenKey VCVS 2nd
order LP &HP
filters
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
Unity Gain Sallen-Key VCVS
• Most basic active filter with unity gain, second-order
• fc for both HP and LP unity gain VCVS with Butterworth response is
given by filter
fc = 1/[2πSqrt(C1C2R1R2)]
• If α is other than 1.414, appropriate Kf should be included in fc
• LP: H(jf) dB = 20 log [1/{Sqrt(1+(α2-2)(f/fc)2+(f/fc)4}]
• HP: H(jf) dB = 20 log [1/{Sqrt(1+(α2-2)(fc/f)2+(fc/f)4}]
• Normalization: to set α of an LP unity gain VCVS to a desired value
and produce a fc of 1 rad/s, we set R1=R2=1 Ω and C1 = 2/α farads, C2
= α/2 farads
• Frequency and impedance scaling are used to produce a useful
design
Unity Gain Sallen-Key VCVS
• Impedance Scaling: to scale impedance while
maintaining a constant fc, multiply all resistors by the
scale factor and divide all capacitors by same scale
factor; impedance scaling factor Kz = Znew/Zold
• Frequency Scaling: to scale frequency while
maintaining a constant impedance, divide all capacitors
by frequency scaling OR by multiplying all resistors by
scaling factor, while leaving capacitors at a give value;
impedance scaling factor Kf = fnew/fold
• In order to obtain a useful form of HP unity gain VCVS,
set fc to 1 rad/s and capacitors are made equal at 1
farad, while R1 = α/2 and R2 = 2/α
Equal-Component Sallen-Key VCVS
• Although unity gain VCVS filters get maximum
bandwidth form op amp, they are little difficult to
design and analyze
• Also strict component ratios must be maintained;
rather difficult to vary parameters of filter
independently
• Equal-component Sallen-Key VCVS filters provide
quite effective solutions
– Designed using equal-values frequency-determining
components (R1 = R2 and C1 = C2)
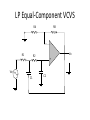
LP Equal-Component VCVS
RB
RA
R1
Vo
R2
Vin
C1
+
C2
LP Equal-Component VCVS
• Gain of circuit is determined by RA and RB, that are
generally not equal
• Design of equal-component VCVS requires the gain of op
amp to be set at some value that produces desired α
• Assuming Butterworth response
fc = 1/[2πSqrt(C1C2R1R2)]
fc = 1/(2πRC) (since R= R1 = R2 , C= C1 = C2)
• LP filter may be converted to HP filter with same fc by
swapping positions of resistors R1 and R2 with capacitors C1
and C2
• Av = 3 – α
• RB = RA (2 – α)
Second-Order Equal-Component VCVS
• Analysis of second-order equal-component
VCVS requires a reverse application of design
procedure
– Determine the passband gain of filter and
calculate α; response type is determined by
comparing the calculated α with those listed for
common filter responses
– Apply appropriate frequency scaling factor to fc =
1/(2πRC), and calculate corner frequency of filter
•
•
•
•
•
Higher-Order
LP
and
HP
Filters
Active filters with orders of greater than two are
obtained by cascading first- and second-order
sections as required
Overall order of a filter that is designed in this
manner is equal to the sum of the orders of
individual sections used
Obtaining a particular response shape is not quite
simple
In order to produce a given response, various
sections used to produce the filter must be
designed with specific α and fc scaling factors taken
into account
When dealing with higher-order filters, all secondorder sections used will be of the equal-component
VCVS types as
– They are easier to analyze and design
– LP-HP conversions are performed simply by swapping
frequency-determining resistors and capacitors
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
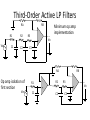
Third-Order LP and HP Filters
• Designed by connecting first-order RC section to second-order section
• Second section will tend to load down first section, producing an overall
response that has slightly greater damping than desired
• Isolating first section eliminates loading effects of second section
• Impedance level of first section should be much lower than that of second
section (scaling impedance of first-order section should be 1/10 of
impedance level of second section)
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
Third-Order Active LP Filters
RA
RB
Minimum op amp
implementation
R1
R2
R3
Vo
+
Vin
C1
C2
C3
RA
RB
-
Op amp isolation of
first section
Vin
R1
-
R2
R3
+
+
C1
C2
C3
Vo
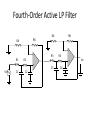
Fourth-Order LP and HP Filters
• Designed by cascading two secondorder filter sections
• Chebyshev filters of order greater than
two will exhibit multiple peaks, or
ripples in passband; higher the order of
filter, more ripples occur
• fc of Chebyshev filter is defined as
frequency at which ripple channel ends
Passband response for
3-dB LP Chebyshev
filters
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
Fourth-Order Active LP Filter
RA
RB
RA
R1
R2
+
Vin
C1
RB
C2
R3
R4
+
C3
C4
Vo
•
•
Bandpass
(BP)
Filters
Active BP and bandstop filters are easily
designed
Advantages over passive BP and bandstop
filters:
Regardless of Q, slope of curve
ultimately approaches a constant value
– Inductorless design
– Ease of tuning and independent parameter
adjustment (Q, f0, and BW), electronic control
of parameters, and option of adjustable
passband gain
•
•
•
•
•
Major performance parameter associated
with BP and bandstop filters is Q (~ 1-20)
Q is reciprocal of filter α
Since α of BP and bandstop filters is very
small, Q is used instead
Q is measure of sharpness of response
around filter center frequency f0
Minimum BP filter order is 2
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
Second-order one-pole BP
normalized response for
various Q’s
Bandpass Filters
•
•
•
•
•
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
BP filters are of even order,
with equal ultimate rolloff
rates on either side of f0
On semilog graph, response
curve will be symmetrical
about f0
Continent way of visualizing
relationship between order of
BP filter and its amplitude
response curve is to assume
that on each side of f0,
ultimate rolloff rate will be
that of a HP or LP filter of
one-half the order of BP filter
Second-order BP has one
pole, fourth-order BP has two
poles, and so on
fc (LP section) > fc (HP section)
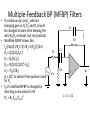
Multiple-Feedback BP (MFBP) Filters
• Most applications using BP filters
requires Q to be higher than unity
• MFBP is one-op amp circuit with a
second-order, single-pole amplitude
response characteristic
• Center frequency
f0 = 1/[2πSqrt(C1C2R1R2)]
• To ease component selection and to
reduce number of variables
C = C 1 = C2
• For design purposes, values of
resistors, based on desired filter
characteristics, are determined
R1 = Q/(2πf0AvC)
R2 = Av/(2πf0QC)
• Passband Av = -Q Sqrt(R2/R1)
C2
R2
R1
C1
-
Vin
+
Vo
Multiple-Feedback BP (MFBP) Filters
• To continuously vary f0 without
changing gain or Q, R1 and R2 should
be changed at same time keeping the
ratio R2/R1 constant; but not practical
• Modified MFBP allows this
f0=[Sqrt{(1/R2C2)(1/R1+1/R3)}]/(2π)
R1 = Q/(2πf0AvC)
R2 = Q/(πf0C)
R3 = Q/[2πf0C(2Q2-Av)]
Av = -R2/(2R1)
Av < 2Q2 to obtain finite positive value
for R3
• f0 of modified MFBP is changed by
selecting a new value for R3
R’3 = R3 (fold/fnew)2
C2
R2
R1
C1
R3
Vin
+
C = C1 = C2
Vo
Multiple-Feedback BP (MFBP) Filters
C2
R2
R1
C1
-
Vin
R3
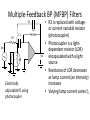
Electrically
adjustable f0 using
photocoupler
+
Vo
• R3 is replaced with voltageor current-variable resistor
(photocoupler)
• Photocoupler is a lightdependent resistor (LDR)
encapsulated with a light
source
• Resistance of LDR decreases
as lamp current (an intensity)
increases
• Varying lamp current varies f0
Multiple-Feedback BP (MFBP) Filters
• JFET can also be used as
voltage-controlled resistor
Electrically adjustable
• Negative control voltage
f0 using a JFET
applied to gate drives JFET
toward pinchoff, increasing
drain-to-source resistance
C2
Vc is negative
• To use JFET effectively, VDS
with respect to
R2
(and input voltage) should be ground
C1
R1
held to a maximum of about
500 mVP-P
Vin
• For voltages within these
R3
D
limits, JFET will act essentially
G
+
Vc
like a linear resistance whose
S
value is dependent on VGS
Vo
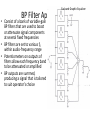
BP Filter Applications
• Displays amplitudes of different
•
•
•
•
Spectrum Analyzer
•
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
frequency components that comprise
a signal
A sweep oscillator varies f0 of BP and
also drives horizontal input of an
oscilloscope
Output of BP filter is amplified and
rectified, and applied to vertical input
of scope
Frequency components that exist in
input signal are filtered out at
different times during a sweep
causing peaks to appear on scope
Horizontal scale of scope represents
frequency, while vertical scale
represents voltage
Changes in frequency content of
input signal are not shown at all
points in time
Six-band Graphic Equalizer
BP Filter Applications
• Consist of a bank of variable-gain
BP filters that are used to boost
or attenuate signal components
at several fixed frequencies
• BP filters are set to various f0
within audio-frequency range
• Potentiometers on outputs of
filters allow each frequency band
to be attenuated or amplified
• BP outputs are summed,
producing a signal that is tailored
to suit operator’s choice
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
BP Filter Applications
Response curves for graphic
equalizer
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
• Filters have Q’s ~ 2 producing
identically shaped response
curves on semilog graph
• Relative low Q is desirable, so
that there are no large
“holes” or gaps in audio
spectrum (20 Hz -20 KHz)
• If more filters were used,
higher-Q filters could be used
• Spectrum is not divided
linearly, but rather in a
logarithmic manner
Bandstop (notch or band-reject) Filters
•
•
•
•
•
•
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
Used to reject or attenuate undesired
frequency components
Bandstop response can be produced by
summing outputs of HP and LP filters
with overlapping amplitude response
curves
Main idea is to set fc for LP filter at a
higher frequency than for HP filter
Bandstop response of this circuit makes
sense only when phase response curves
of HP and LP filters are considered as
well as their amplitude response curves
Outputs of HP and LP filters are always
out of phase by 180°
Critical point occurs when f = f0 where
outputs of filters are equal in amplitude
and 180° out of phase resulting in
cancellation of signals at output of
summer
Bandstop (notch or band-reject) Filters
•
Bandstop
•
implemented using
second-order equalcomponent VCVS
•
filters
•
•
•
•
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
Since outputs are being summed and
since one filter will be producing output
voltage of much grater amplitude for
frequencies on either side of f0, two
passbands are produced
To produce predictable response, both
filters should be of same order with same
response shape (usually Butterworth)
Q is determined in same manner as for
BP filter
For highest Q, the HP and LP filters
should have identical fc
Null frequency is determined by Eq. 6.7
Maximum rejection is ~ 50 dB below
passband gain
Overall gain (in dB) at f0 is called null
depth; greater the null depth, more
effective the filter
Bandstop (notch or band-reject) Filters
Second bandstop filter that
relies on cancellation of
phase-shifted signals for its
response characteristics
• Due to inverting gain of MFBP filter, output signal is 180° out of
phase with input at f0
• When output of MFBP is summed with input signal, it is possible
to obtain a bandstop response due to the relative phase inversion
of two signals
• Null frequency of bandstop is same as f0 for MFBP
• To realize maximum null depth, summing amplifier must be
designed to compensate for differences between its tow input
signals
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
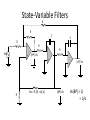
State-Variable Filters
R
R
R
Vin
+
C
R
-
C
R
(HP) Vo
+
+
R
Rα = R [(3- α)/ α]
(BP) Vo
(LP) Vo
Av(BP) = Q
= 1/α
State-Variable Filters
•
•
•
•
•
•
•
•
•
State-variable filter is an analog computer that continuously
solves a second-order differential equation
State-variable filter produces simultaneous HP, LP, and BP
responses
For HP and LP outputs, any practical second-order response
shape can be achieved, while for BP output, Q’s of greater
than 100 are easily obtained
Can be constructed using three or more op amps
Both integrators use equal-value components, and for
convenience, remaining resistors are set equal to integrator
resistors or scaled as necessary
fc of HP and LP outputs and f0 of BP output: f0 = 1/(2πRC)
f0 can be varied continuously, without affecting α or Q, by
simultaneously varying integrator input resistors while keeping
then equal to each other
Passband gain of HP and LP outputs is unity
For BP output, gain at f0 is Av(BP) = Q = 1/α
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
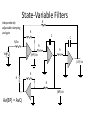
State-Variable Filters
R
Independently
adjustable damping
and gain
R/Av
Vin
R
-
C
R
-
C
R
(HP) Vo
+
+
+
R
R
-
R
(BP) Vo
Av(BP) = AvQ
+
(LP) Vo
All-Pass Filters
•
•
•
•
•
•
•
•
Designed to provide constant gain to signals at all frequencies
Ideally, cover entire frequency spectrum
Flat amplitude response characteristic is quite different from those of other filters (LP, HP, BP,
notch)
Produce an output that is shifted in phase relative to input signal
Figure: Output signal leads that of input
For frequencies approaching 0, phase lead approaches 180°
As frequency increases, phase lead of output approaches 0
Phase angle: Ø = 2 tan-1 [1/(2πfR1C1)]
Operational Amplifiers and Linear
Integrated Circuits: Theory and Applications
by Denton J. Dailey
All-Pass Filters
• Feedback and inverting input resistors must be equal to each other
• Absolute values of resistors is not critical, but for minimum offset, parallel
equivalent of these two resistors should nearly equal the value of R1
• Gain of all-pass filter is unity (a necessary condition for normal operation)
• By replacing R1 with a potentiometer (or equivalent voltage-controlled
resistance), phase angle of output may be varied continuously
• Cascading similar all-pass sections produces and additive phase shift
• Two all-pass filters cascaded will approach a maximum phase shift of 360°,
three sections will approach a maximum phase shift of 540°,..
• Lagging phase angle may be produced by interchanging R1 and C1 with the
phase angle: Ø = -2 tan-1 (2πfR1C1)