Download Sequences as Functions

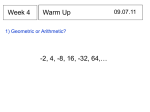
Solutions to Tasks
Function Notation
Part 1
One vacation when visiting his grandmother, Todd found markings on the inside of a closet
door showing the heights of his mother, Julia, and her brothers and sisters on their
birthdays growing up. From the markings in the closet, Todd wrote down his mother’s
height from ages 2 to 16. His grandmother found the measurements at birth and one year
by looking in his mother’s baby book. The data is provided in the table below, with heights
rounded to inches.
Age (yrs.)
x
Height (in.) y = h(x)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
21 30 35 39 43 46 48 51 53 55 59 62 64 65 65 66 66
1. Which variable is the independent variable, and which is the dependent variable?
Explain your choice.
Age is the independent variable and height is the dependent variable because height
depends on age.
2. Make a graph of the data on a separate piece of paper.
3. Should you connect the dots on your graph? Explain.
Yes, Julia’s height continued to increase between the measurements, but connecting the
dots only gives an approximation of what happened between measurements.
4. Describe how Julia’s height changed as she grew up.
Answers will vary.
5. How tall was Julia on her 11th birthday? Explain how you can see this in both the
graph and the table.
Julia was 62 inches on her 11th birthday. When x is 11 on both the table and the graph,
h(x) is 62.
6. What do you think happened to Julia’s height after age 16? Explain. How could you
show this on your graph?
Julia’s height probably didn’t change much after age 16. She may have grown a little, but
most girls are finished growing by the time they are 16. The graph would likely level off
after 16 (become horizontal).
Function Notation
Part 2
Answer the next set of questions using this data from Part 1.
Age (yrs.)
x
Height (in.) y = h(x)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
21 30 35 39 43 46 48 51 53 55 59 62 64 65 65 66 66
1. What is h(11)? What does this mean?
h(11)=62. This means that Julia’s height at age 11 was 62 inches.
2. When x is 3, what is y? Express this fact using function notation.
h(3)=43.
3. Find an x so that h(x) = 53. Explain your method. What does your answer mean?
h(x)=53 when x=8. I found that by looking across the y values where I saw y is 53 when x
is 8.
4. From your graph or your table, estimate h(6.5). Explain your method. What does
your answer mean?
I averaged the values for h(6) and h(7). So at age 6.5, Julia was approximately 49.5 inches
tall. This is an approximation because I don’t really know how Julia’s height changed from
month to month within a year.
5. Find an x so that h(x) = 60. Explain your method. What does your answer mean?
I estimated x to be about 10.33. Since 60 is 1/3 the distance from 59 to 62, I added 1/3 to
the age that Julia was when she was 59 inches tall (10 years old).
6. Describe what happens to h(x) as x increases from 0 to 16.
Overall, x increases, but the graph shows periods where the increase is steeper (or quicker)
than other periods (like growth spurts).
7. What can you say about h(x) for x greater than 16?
I don’t know exactly what happens for values of x greater than 16. I would assume, since
this is height of a girl, that the values would not increase much after age 16 (if they
increase at all). Students will probably mention that at some point in the future her height
might even decrease slightly.
8. Describe the similarities and differences you see between these questions and the
questions in the previous section.
The questions in both sections are ultimately asking the same things. One section has a
more apparent context and the other section is asking the same questions using
mathematical language.
Function Notation
Part 3
When Peachtree Plains High School opened in 2001, a few teachers and students put on
FallFest, featuring contests, games, prizes, and performances by student bands. To raise
money for the event, they sold FallFest T-shirts. The event was very well received, and so
FallFest has become a tradition. The graph below shows T-shirt sales for each FallFest so
far.
70
S(t),
# of
shirts
60
50
40
30
20
10
t, in years
2
4
1. What are the independent and dependent variables shown in the graph?
The independent variable is time, in years, and the dependent variable is number of shirts
sold.
2. For which years does the graph provide data?
The graph provides data from 2001 to 2005.
3. Does it make sense to connect the dots in the graph? Explain.
No, sales only occurred once each year. This is a good time to recognize the difference
between discrete and continuous data. If we were to create a line of best fit, it would give
the appearance that the shirt sales occurred continuously throughout the year. However, in
actual practice, we do this a lot in order to make reasonable predictions for the future.
4. What were the T-shirt sales in 2001? Use function notation to express your result.
S(1)=42
5. Find S(3), if possible, and explain what it means or would mean.
S(3)=78. This means that in 2003, 78 t-shirts were sold at the FallFest.
6. Find S(6), if possible, and explain what it means or would mean.
S(6) is only a prediction. It has not occurred yet. Any value we assigned to S(6) would be
a prediction for future sales, so it could only be an estimate. We would probably want to
create a graph like this just so that we could make a reasonable estimate for 2006 sales.
7. Find S(2.4), if possible, and explain what it means or would mean.
S(2.4) is not possible. Since the sales only occur once each year, a value between years is
not possible. S(2.4) would represent the sales for the end of April 2002 (4/10 of the year).
8. If possible, find a t such that S(t) = 65. Explain.
In 2004, they sold 65 t-shirts, so S(4)=65.
9. If possible, find a t such that S(t) = 62. Explain.
This is not possible with the current data. There were no years where exactly 62 t-shirts
were sold at the FallFest.
10. Describe what happens to S(t) as t increases, beginning at t = 1.
For t=1 to t=2, sales climbed dramatically. For t=2 to t=3, sales climbed, but not as
steeply. For t=3 to t=4, sales dropped a little. For t=4 to t=5, sales climbed a bit again. If
I were going to use this to decide how many t-shirts to order for the next FallFest, I would
probably order about 75 shirts. The graph appears to be climbing (I might check to see
why the decline in 2004), but not at a great rate anymore.
Using the graph to predict for 2006 may cause some students concern. They may not like
using it to predict because there aren’t very many data points. They also may express
concern over how outside factors would impact sales (weather, t-shirt design, student
population, other events in the community). These are all good points for discussion.
11. What can you say about S(t) for values of t greater than 6?
While we would likely use our graph to predict for 2006, it is unlikely that it would be safe to
use it for 2007 and beyond. This is called “extrapolation” and it is unwise to extrapolate too
far out of the range of the data we have. Considering our sample size is very small,
extrapolating would be very dangerous.
Function Notation
Part 4
Suppose a ball is dropped from a high place, such as the Tower of Pisa. If y, measured in
meters, is the distance the ball has fallen and x, measured in seconds, is the time since the
ball was dropped, then y is a function of x, and the relationship can be approximated by the
formula y = f(x) = 5x2.
x
0
1
2
3
4
5
6
…
x2
0
1
4
9
16
25
36
…
y = f(x) = 5x2
0
5
20
45
80
125
180
…
1. Fill in the missing values in the table above.
2. Suppose the ball is dropped from a building at least 100 meters high. Measuring
from the top of the building, draw a picture indicating the position of the ball at times
indicated in your table of values.
Answers will vary, but the graph should visually show the ball dropping.
3. Draw a graph of x versus y for this situation on a separate piece of paper. Should
you connect the dots? Explain.
A graph on the coordinate plane of x versus y appears to show the ball climbing.
Connecting the dots is appropriate because this is continuous data. The ball continues to
drop between measurements.
4. What is the relationship between the picture (#2) and the graph (#3)?
The picture in #2 represents the location of the ball at any given moment, so it clearly
expresses the downward motion of the ball. The graph is representing the distance traveled
which is increasing as gravity pulls the ball faster. The graph appears to show the ball
climbing.
5. You know from experience that the speed of the ball increases as it falls. How can
you “see” the increasing speed in your table? How can you “see” the increasing
speed in your picture?
In the graph, it appears that the “slope” or rate of change is getting steeper. In the picture,
the distance from one point to the next is growing.
6. What is f(4)? What does this mean?
f(4)=80 which means that at 4 seconds the ball has traveled 80 meters.
7. Estimate x such that f(x) = 50. Explain your method. What does it mean?
x=3.16. After 3 seconds, the ball has dropped 50 meters.
8. In this context, y is proportional to x2. Explain what that means. How can you see
this in the table?
The proportion of
y
y
5
is the same for every pair of points.
2
x
x2
Function Notation
Part 5
Towanda is paid $7 per hour in her part-time job at the local Dairy Stop. Let t be the
amount time that she works, in hours, during the week, and let P(t) be her gross pay
(before taxes), in dollars, for the week.
1. Make a table showing how her gross pay depends upon the amount of time she
works during the week.
t
1
2
3
4
5
P(t)
7
14
21
28
35
2. Make a graph illustrating how her gross pay depends upon the amount of time that
she works. Should you connect the dots? Explain.
You should connect the dots because she can work a
portion of an hour.
3. Write a formula showing how her gross pay depends upon the amount of time that
she works.
P(t) = 7t
4. What is P(9)? What does it mean? Explain how you can use the graph, the table,
and the formula to compute P(9).
P(9)=63. She will make $63 if she works 9 hours.
5. If Towanda works 11 hours and 15 minutes, what will her gross pay be? Show how
you know. Express the result using function notation.
P(11.25) = 78.75
6. If Towanda works 4 hours and 50 minutes, what will her gross pay be? Show how
you know. Express the result using function notation.
P(4.8333)=33.83
7. One week Towanda’s gross pay was $42. How many hours did she work? Show how
you know.
42 = 7t
t=6
She worked six hours.
8. Another week Towanda’s gross pay was $57.19. How many hours did she work?
Show how you know.
57.19 = 7t
t = 8.17
She worked 8 hours and 10 minutes.
Sequences as Functions
In your previous study of functions, you have seen examples that begin with a
problem situation. In some of these problem situations you needed to extend and
generalize a pattern. In the following problems, you will explore patterns as
sequences and how sequences are functions.
A sequence is an ordered list of numbers, pictures, letters, geometric figures, or
just about any object you like. Each number, figure, or object is called a term in
the sequence. For convenience, the terms of sequences are often separated by
commas. In Math 1, we will focus mostly on sequences of numbers, and we will
often use geometric figures and diagrams as illustrations and as contexts for
investigating various number sequences.
1. Some sequences follow predictable patterns, though the pattern might not
be immediately apparent. Other sequences have no pattern at all. Explain,
when possible, patterns in the following sequences:
a. 5, 4, 3, 2, 1
subtract 1 each time
b. 3, 5, 1, 2, 4
no pattern
c. 2, 4, 3, 5, 1, 5, 1, 5, 1, 5, 1, 7
no pattern
d. S, M, T, W, T, F, S
days of the week
e. 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31
number of day in a month
f. 1, 2, 3, 4, 5, …, 99, 100
add one each time
g. 1, 3, 5, 7, 9, 11, …
odd numbers or add two each time
h. 4, 7, 10, 13, 16, …
add three each time
i. 1, 4, 9, 16, 25, …
squared numbers
For the sequences below, assume that the sequence begins with an index value
of 1. You will see later that it is sometimes useful, depending on the context or for
ease of calculation, to specify a starting index value other than 1.
2. Assuming that the sequences continue in the simplest possible way, find the
13th, 100th, and nth term of each sequence.
a. 1, 3, 5, 7, 9, 11, …
13th term is 25; 100th term is 199; nth term is 2n-1
b. 4, 7, 10, 13, 16, …
13th term is 40; 100th term is 301; nth term is 3n+1
Sequence
2, 4, 6, 8, 10, …
8, 11, 14, 17, 20, …
Recursive formula
NEXT = NOW + 2
NEXT = NOW + 3
Closed formula
f(n) = 2n
f(n) = 3n + 5
3. A sequence has a beginning term of 1 and recursive formula
NOW = NEXT + 3.
a. Write the first several terms of this sequence.
1, 4, 7, 10, 13, 16, ….
b. Find a closed formula for this sequence.
3n-2
c. Find a different sequence that uses the same recursive formula.
2, 5, 8, 11, 14, …
4. Write recursive formulas for the following sequences, assuming the patterns
continue in the simplest possible way. Remember that recursive formulas
require specification of the starting term(s).
a. 2, 6, 10, 14, …
a1  2
a n  a n 1  4
a1  2
b. 2, 6, 18, 54, …
a n  3  a n 1
a1  1
c. 1, 1, 2, 3, 5, 8, …
a2  1
a n  a n 1  a n  2
d. 0, 3, 8, 15, 24, …
a1  0
a n  a n 1  2n  1
e. 1, 3, 6, 10, 15, …
a1  1
a n  a n 1  n
5. Find recursive formulas and closed formulas for the following sequences,
assuming the sequences begin with the first term.
a. 1, 3, 5, 7, 9, 11, …
a1  1
a n  2n  1
a n  a n 1  2
b. 4, 7, 10, 13, 16, …
a1  4
an  3n  1
a n  a n 1  3
6. Consider the sequence of dot figures below.
…
n=1
n=2
n=3
n=4
n=5
a. The sequence continues so that the number of dots in each figure is the
next square number. Why are these numbers called square numbers?
b. What is the next figure in the sequence? What is the next square
number?
A 6 x 6 square of dots, so the next square number is 36.
625
c. What is the 25th square number? Explain.
d. Is 156 a square number? Explain.
No. The square root of 156 is not a whole number.
e. Let g be a function that gives the number of dots in the nth figure in the
following sequence. Write a formula for this function.
g n   n 2
f. On a separate piece of paper make a graph and a table for the function g.
g. What is the domain of the function g (in the context)?
natural numbers
h. What is the range of the function g?
perfect squares greater than 0
7. Consider a function f that gives the area of a square of side-length s, shown
below.
s
a. What is the area of a square of side length 6?
36
b. Find a formula for the function f.
f s   s 2
c. On a separate piece of paper, make a graph and a table for the function f.
d. Use your formula to find the area of squares with the following side
lengths: 7, 1/2, 1.2, 3 , and 200.
f 7   49
1 1
f 
2 4
f 1.2   1.44
f
 3  3
f 200   40,000
e. What is the domain of f (in the given context)?
all real numbers greater than 0 or 0, 
f. What are the limiting case(s) in this context? Explain.
You cannot have a side of 0 or less.
8. Compare the functions g and f from the previous two problems.
a. Explain how similarities and differences in the formula, table, and graph
arise from similarities and differences in the contexts.
Answers will vary.
b. Are these functions equal? Explain.
No, g is only natural numbers while f is real numbers.