* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture13b
Survey
Document related concepts
Transcript
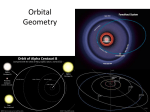
Sect. 13.3: Kepler’s Laws & Planetary Motion Johannes Kepler • German astronomer (1571 – 1630) • Spent most of his career tediously analyzing huge amounts of observational data (most compiled by Tycho Brahe) on planetary motion (orbit periods, orbit radii, etc.) • Used his analysis to develop “Laws” of planetary motion. “Laws” in the sense that they agree with observation, but not true theoretical laws, such as Newton’s Laws of Motion & Newton’s Universal Law of Gravitation. Kepler’s “Laws” Kepler’s “Laws” are consistent with & are obtainable from Newton’s Laws • Kepler’s First Law – All planets move in elliptical orbits with the Sun at one focus • Kepler’s Second Law – The radius vector drawn from the Sun to a planet sweeps out equal areas in equal time intervals • Kepler’s Third Law – The square of the orbital period of any planet is proportional to the cube of the semimajor axis of the elliptical orbit Math Review: Ellipses • The points F1 & F2 are each a focus of the ellipse – Located a distance c from the center – Sum of r1 and r2 is constant • Longest distance through center is the major axis, 2a a is called the semimajor axis • Shortest distance through center is the minor axis, 2b Typical Ellipse b is called the semiminor axis • The eccentricity is defined as e = (c/a) – For a circle, e = 0 – The range of values of the eccentricity for ellipses is 0 < e < 1 – The higher the value of e, the longer and thinner the ellipse Ellipses & Planet Orbits • The Sun is at one focus – Nothing is located at the other focus • Aphelion is the point farthest away from the Sun – The distance for aphelion is a + c • For an orbit around the Earth, this point is called the apogee • Perihelion is the point nearest the Sun – The distance for perihelion is a – c • For an orbit around the Earth, this point is called the perigee Kepler’s 1st Law All planets move in elliptical orbits with the Sun at one focus • A circular orbit is a special case of an elliptical orbit – The eccentricity of a circle is e = 0. • Kepler’s 1st Law can be shown (& was by Newton) to be a direct result of the inverse square nature of the gravitational force. Comes out of N’s 2nd Law + N’s Gravitation Law + Calculus • Elliptic (and circular) orbits are allowed for bound objects – A bound object repeatedly orbits the center – An unbound object would pass by and not return • These objects could have paths that are parabolas (e = 1) and hyperbolas (e > 1) Orbit Examples • Fig. (a): Mercury’s orbit has the largest eccentricity of the planets. eMercury = 0.21 Note: Pluto’s eccentricity is ePluto = 0.25, but, as of 2006, it is officially no longer classified as a planet! • Fig. (b): Halley’s Comet’s orbit has high eccentricity eHalley’s comet = 0.97 • Remember that nothing physical is located at the second focus – The small dot Kepler’s 2nd Law The radius vector drawn from the Sun to a planet sweeps out equal areas in equal time intervals • Kepler’s 2nd Law can be shown (& was by Newton) to be a direct result of the fact that N’s Gravitation Law gives Conservation of Angular Momentum for each planet. • The Gravitational force produces no torque (it is to the motion) so that Angular Momentum is Conserved: L = r x p = MPr x v = constant Kepler’s 2nd Law • Geometrically, in a time dt, the radius vector r sweeps out the area dA = half the area of the parallelogram • The displacement is dr = v dt L • Mathematically, this means dA constant dt 2Mp • That is: the radius vector from the Sun to any planet sweeps out equal areas in equal times Kepler’s 3rd Law The square of the orbital period T of any planet is proportional to the cube of the semimajor axis a of the elliptical orbit • If the orbit is circular & of GMSunMPlanet MPlanetv 2 radius r, this follows from 2 r r Newton’s Universal 2 r Gravitation. v T • This gravitational force 2 supplies a centripetal force 3 4 2 3 T r K r S for user in GMSun Newton’s 2nd Law Ks is a constant, which • Ks is a constant is the same for all planets. Kepler’s 3rd Law • Can be shown that this also applies to an elliptical orbit with replacement of r with a, where a is the semimajor axis. 2 3 4 2 3 T a K a S GMSun • Ks is independent of the planet mass, & is valid for any planet • Note: If an object is orbiting another object, the value of K will depend on the mass of the object being orbited. For example, for the Moon’s orbit around the Earth, KSun is replaced with KEarth, where KEarth is obtained by replacing MSun by MEarth in the above equation. Solar System Data Table 13-2, p. 370 “Weighing” the Sun! • We’ve “weighed” the Earth, now lets “weigh” the Sun!! Assume: Earth & Sun are perfect uniform spheres. & Earth orbit is a perfect circle. • Note: For Earth, Mass ME = 5.99 1024kg Orbit period is T = 1 yr 3 107 s Orbit radius r = 1.5 1011 m So, orbit velocity is v = (2πr/T), v 3 104 m/s • Gravitational Force between Earth & Sun: Fg = G[(MSME)/r2] Circular orbit is circular centripetal acceleration Newton’s 2nd Law gives: ∑F = Fg = MEa = MEac = ME(v2)/r OR: G[(MSME)/r2] = ME(v2)/r. If the Sun mass is unknown, solve for it: MS = (v2r)/G 2 1030 kg 3.3 105 ME