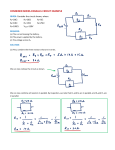
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download ch20_sol
Operational amplifier wikipedia , lookup
Power electronics wikipedia , lookup
Negative resistance wikipedia , lookup
Lumped element model wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Surge protector wikipedia , lookup
Opto-isolator wikipedia , lookup
Electrical ballast wikipedia , lookup
Current source wikipedia , lookup
Power MOSFET wikipedia , lookup
Rectiverter wikipedia , lookup
Current mirror wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
CHAPTER 20 ELECTRIC CIRCUITS CONCEPTUAL QUESTIONS ____________________________________________________________________________________________ 1. REASONING AND SOLUTION a. When S1 is set to position A, current can flow from the generator only along the path that requires S2 to be set to position A. Hence, the light will be on when S2 is in position A. b. When S1 is set to position B, current can flow from the generator only along the path that requires S2 to be set to position B. Hence, the light will be on when S2 is in position B. ______________________________________________________________________________ 2. REASONING AND SOLUTION When an incandescent light bulb is turned on, the tungsten filament becomes white hot. Since the voltage is constant, the power delivered to 2/R V the light bulb is given by Equation 20.6c: P . From Equation 20.5, RR 0 [ 1 ( TT 0 ) ], where is the temperature coefficient of resistivity and is a positive number. Thus, as the filament temperature increases, the resistance of the wire increases, and as the filament heats up, the power delivered to the bulb decreases. ____________________________________________________________________________________________ 3. SSM REASONING AND SOLUTION Two materials have different resistivities. Two wires of the same length are made, one from each of the materials. The resistance of each wire is given by Equation 20.3: R L/ A, where is the resistivity of the wire material, and L and A are, respectively, the length and cross-sectional area of the wire. Even when the wires have the same length, they may have the same resistance, if the cross-sectional areas of the wires are chosen so that the ratio L / A is the same for each. ____________________________________________________________________________________________ 4. REASONING AND SOLUTION The resistance of a wire is given by Equation 20.3: R L/ A, where is the resistivity of the wire material, L is the length of the wire, and A is its cross-sectional area. Since the cross-sectional area is proportional to the square of the diameter, a doubling of the diameter causes the cross-sectional area to be increased fourfold. From Equation 20.3, we see that doubling both the diameter and length causes the resistance of the wire to be reduced by a factor of 2. ____________________________________________________________________________________________ 5. REASONING AND SOLUTION One electrical appliance operates with a voltage of 120 V, while another operates with a voltage of 240 V. The power used by either appliance is given 2/R V by Equation 20.6c: P . Without knowing the resistance R of each appliance, no conclusion can be reached as to which appliance, if either, uses more power. ____________________________________________________________________________________________ Chapter 20 Conceptual Questions 6. 7 REASONING AND SOLUTION Two light bulbs are designed for use at 120 V and are rated at 75 W and 150 W. The power used by either bulb is given by Equation 20.6c: 2/R P V . We see from Equation 20.6c that, at constant voltage, the power used by a bulb is inversely proportional to the resistance of the filament. Therefore, the filament resistance is greater for the 75-W bulb. ____________________________________________________________________________________________ 7. REASONING AND SOLUTION Rather than state how many watts of power an appliance uses, appliance instructions often give statements such as "10 A, 120 V" instead. This statement gives the current used by the appliance for a specific voltage. It provides all the information necessary to determine the power usage of the appliance from Equation 20.6a: P = IV. Thus, the "current-voltage" rating given in the instructions is equivalent to a statement of the power consumption of the appliance. ____________________________________________________________________________________________ 8. REASONING AND SOLUTION When the switch is initially closed, a current appears in the circuit, because charges flow through the heater wire, the bimetallic strip, the contact point, and the light bulb. The bulb glows in response. As charges flow through the heater wire, it becomes hot thereby heating the bimetallic strip. As the strip is heated, the brass, having a larger coefficient of thermal expansion, expands more than the steel. Thus, the bimetallic strip bends into an arc away from the contact point, and the electric current drops to zero because the charges no longer have a continuous path along which to flow. The bulb ceases to glow. Since there is no longer a current, the resistance wire, and hence, the bimetallic strip begin to cool down to room temperature. As the bimetallic strip cools, it bends back to its initial position, as shown in the drawing in the text. When it reaches room temperature it will again touch the contact point, and a current will begin to flow again. The wire and the bimetallic strip will become hot and the bimetallic strip will bend away from the contact point and the current will again drop to zero. This cycle will continue as long as the switch remains closed. Therefore, as long as the switch remains closed, the bulb will flash on and off. ____________________________________________________________________________________________ 9. REASONING AND SOLUTION The power rating of a 1000-W heater specifies the power consumed when the heater is connected to an ac voltage of 120 V. The power consumed by 2 the heater is given by Equation 20.6c: P . When two of these heaters are connected 1V/R in series, the equivalent resistance of the combination is R + R = 2R. The power consumed by two of the heaters connected in series is, therefore, 2 P (2 R )P / 2= ( 1 0 0 0 W ) / 2= 5 0 0 W . 2V/ 1 ____________________________________________________________________________________________ 10. SSM REASONING AND SOLUTION A number of light bulbs are to be connected to a single electrical outlet. The bulbs will provide more brightness when they are connected in such a way that their power output is greatest. Since the voltage at the outlet is constant, the 2/R V power delivered by the bulbs is given by Equation 20.6c: P , where R is the equivalent resistance of the combination of light bulbs. When the light bulbs are connected .. SR 1R 2R 3. in series, their equivalent resistance is given by Equation 20.16: R 8 ELECTRIC CIRCUITS When the light bulbs are connected in parallel, their equivalent resistance is given by 1 1 1 1 Equation 20.17: R R R R... Clearly, the equivalent resistance will be less P 1 2 3 when the bulbs are connected in parallel. From Equation 20.6c, we can conclude that the power output will be greatest, and the light bulbs will provide more brightness, when they are connected in parallel. ____________________________________________________________________________________________ 11. REASONING AND SOLUTION A car has two headlights. The filament of one burns out. However, the other headlight stays on. We can immediately conclude that the bulbs are not connected in series. The figure below shows the series arrangement of two such bulbs. Bulb with burned out filament When the bulbs are connected in series, charges must flow through the filaments of both lights in order to have a complete circuit. Since the filament of the second bulb is burned out, charges will not be able to flow around the circuit, and neither headlight will stay on. On the other hand, if the bulbs are J connected in parallel, as shown at the right, the current will split at the junction J. Charges will be able to flow through the branch of the circuit that contains the good bulb, and that headlight will stay on. Notice that the order of the bulbs does not matter in either case. The results are the same. Bulb with burned out filament ____________________________________________________________________________________________ 12. REASONING AND SOLUTION When two or more circuit elements are connected in series, they are connected such that the same electric current flows through each element. When two or more circuit elements are connected in parallel, they are connected such that the same voltage is applied across each element. The circuit in Figure (a) can be shown to be a combination of series and parallel arrangements of resistors. The circuit can be redrawn as shown in the following drawing. Chapter 20 Conceptual Questions 9 3 2 3 4 4 7 2 7 5 5 6 1 8 8 6 1 We can see in the redrawn figure that the current through resistors 2 and 3 is the same; therefore, resistors 2 and 3 are in series and can be represented by an equivalent resistance 23 as shown in the following drawing. 23 3 2 234 4 4 7 5 7 7 5 5 8 6 8 8 6 6 1 1 1 The voltage across resistance 23 and resistor 4 is the same, so these two resistances are in parallel; they can be represented by an equivalent resistance 234. The current through resistance 234 is the same as that through resistor 7, so resistance 234 is in series with resistor 7; they can be represented by an equivalent resistance 2347 as shown in the following figure. 10 ELECTRIC CIRCUITS 2347 23475 234758 5 8 6 6 8 6 1 1 1 The voltage across 2347 is the same as that across resistor 5; therefore, resistance 2347 is in parallel with resistor 5. They can be represented by an equivalent resistance 23475. Similarly, resistance 23475 is in series with resistor 8, giving an equivalent resistance 234758. Resistance 234758 is in parallel with resistor 6, giving an equivalent resistance 2347586. 2347586 Finally, the current through resistor 1 and resistance 2347586 is the same, so they are in series as shown at the right. 1 The circuit in Figure (b) can also be shown to be a combination of series and parallel arrangements of resistors. Since both ends of resistors 2 and 3 are connected, the voltage across resistors 2 and 3 is the same. The same statement can be made for resistors 4 and 5, and resistors 6 and 7. Therefore, resistor 2 is in parallel with the resistor 3 to give an equivalent resistance labeled 23. Resistor 4 is in parallel with resistor 5 to give an equivalent resistance 45, and resistor 6 is in parallel with resistor 7 to give an equivalent resistance 67. From the right-hand portion of the drawing below, it is clear that the resistances 23, 45, and 67 are in series with resistor 1. 2 4 6 23 3 1 5 7 1 45 67 Chapter 20 Conceptual Questions The drawing at the right shows the circuit in Figure (c). No such simplifying arguments can be made for this circuit. No two resistors carry the same current; thus, no two of the resistors are in series. Furthermore, no two resistors have the same voltage applied across them; thus, no two of the resistors are in parallel. Circuit (c) contains resistors that are neither in series nor in parallel. 11 2 1 3 4 5 ____________________________________________________________________________________________ 13. SSM REASONING AND SOLUTION One way is to make two combinations that consist of two resistors in parallel. The resistance of each combination is R R R R R 1 /R )( 1 /R ) 1R /2 p( These two combinations can then be placed in series, as shown at the right. The equivalent resistance of the series combination is R R /2 )(R /2 )R s( A second way is to make two combinations that consist of two resistors in series. The resistance of each combination is R R 2 R sR R R R R These two combinations can then be placed in parallel, as shown at the right. The equivalent resistance of the parallel combination is R 1 /(2 R )1 /( 2 R ) 1R p ____________________________________________________________________________________________ 14. REASONING AND SOLUTION An ammeter is used to measure the current in a particular branch of a circuit, while a voltmeter is used to measure the voltage across two points in a circuit. An ideal ammeter must have a low resistance so that its presence in the circuit does not affect the current measurement. Conversely, an ideal voltmeter must have a large resistance so that it does not draw current and change the voltage between the two points in question. ____________________________________________________________________________________________ 12 ELECTRIC CIRCUITS 15. REASONING AND SOLUTION A voltmeter is inadvertently mistaken for an ammeter and placed in a circuit. A voltmeter is a high resistance instrument. Since an ammeter is placed in series with the circuit, we would be placing a large resistance in series with the circuit, and the resistance of the circuit would greatly increase. From Ohm's law, V = IR, the current in the circuit would drop markedly. ____________________________________________________________________________________________ 16. REASONING AND SOLUTION From Ohm's law, V = IR, 1 ohm = 1 volt/ampere = 1 volt/(coulomb/second). definition of capacitance, q = CV, 1 farad = 1 coulomb/volt. Then From the 1 v o l t 1 c o u l o m b 1 v o l ts e c o n d1 c o u l o m b 1 o h m f a r a d = 1 s e c o n d ( c o u l o m b / s e c o n d ) v o l t c o u l o m b v o l t ____________________________________________________________________________________________ Chapter 20 Problems 13 CHAPTER 20 ELECTRIC CIRCUITS PROBLEMS ______________________________________________________________________________ 1. REASONING AND SOLUTION The definition of current in Equation 20.1 gives q 3 5 C 4 3 .5 1 0 A – 3 t 1 .0 0 1 0s ______________________________________________________________________________ I 2. REASONING The current I is defined in Equation 20.1 as the amount of charge q per unit of time t that flows in a wire. Therefore, the amount of charge is the product of the current and the time interval. The number of electrons is equal to the charge that flows divided by the magnitude of the charge on an electron. SOLUTION a. The amount of charge that flows is q I t 1 8 A 2 . 0 1 0 s 3 . 6 1 0 C 3 2 b. The number of electrons N is equal to the amount of charge divided by e, the magnitude of the charge on an electron. 2 . 6 1 0 C q3 1 7 N 2 . 3 1 0 1 9 e1 . 6 0 1 0 C ______________________________________________________________________________ 3. REASONING AND SOLUTION First determine the total charge delivered to the battery using Equation 20.1: 3 6 0 0 s 5 q I t ( 6 . 0 A ) ( 5 . 0 h ) 1 . 1 1 0 C 1 h To find the energy delivered to the battery, multiply this charge by the energy per unit charge (i.e., the voltage) to get Energy = (q)V = (1.1 105 C)(12 V) = 1.310 J ______________________________________________________________________________ 6 4. REASONING a. According to Ohm’s law, the current is equal to the voltage between the cell walls divided by the resistance. 14 ELECTRIC CIRCUITS + b. The number of Na ions that flows through the cell wall is the total charge that flows divided by the charge of each ion. The total charge is equal to the current multiplied by the time. SOLUTION a. The current is 3 V 7 5 1 0 V 1 1 I 9 1 . 5 1 0 A R 5 . 0 1 0 (20.2) b. The number of Na+ ions is the total charge q that flows divided by the charge +e on each ion, or q / e . The charge is the product of the current I and the time t, according to Equation 20.1, so that 1 1 q I t 1 . 5 1 0 A 0 . 5 0 s + 7 4 . 7 1 0 Number of Na ions = 1 9 ee 1 . 6 0 1 0 C ____________________________________________________________________________________________ I R REASONING AND SOLUTION Ohm's law (Equation 20.2, V ) gives the result directly V2 4 0 V I 2 2 A R1 1 ______________________________________________________________________________ 5. 6. REASONING According to Ohm’s law, the resistance is the voltage of the battery divided by the current that the battery delivers. The current is the charge divided by the time during which it flows, as stated in Equation 20.1. We know the time, but are not given the charge directly. However, we can determine the charge from the energy delivered to the resistor, because this energy comes from the battery, and the potential difference between the battery terminals is the difference in electric potential energy per unit charge, according to Equation 19.4. Thus, a 9.0-V battery supplies 9.0 J of energy to each coulomb of charge passing through it. To calculate the charge, then, we need only divide the energy from the battery by the 9.0 V potential difference. SOLUTION Ohm’s law indicates that the resistance R is the voltage V of the battery divided by the current I, or R = V/I. According to Equation 20.1, the current I is the amount of charge q divided by the time t, or I = q/t. Using these two equations, we have V V V t R I q /t q According to Equation 19.4, the potential difference V is the difference (EPE) in the E PE V electric potential energy divided by the charge q, or . However, it is q customary to denote the potential difference across a battery by V, rather than V, so Chapter 20 Problems 15 EPE E PE V q . Solving this expression for the charge gives . Using this result q V in the expression for the resistance, we find that 2 9 . 0 V 6 3 6 0 0 s V t V t V t R 1 6 5 q E P E / V E P E 1 . 1 1 0 J 2 7. REASONING As discussed in Section 20.1, the voltage gives the energy per unit charge. Thus, we can determine the energy delivered to the toaster by multiplying the voltage V by the charge q that flows during a time t of one minute. The charge can be obtained by solving Equation 20.1, I = (q)/(t), since the current I can be obtained from Ohm’s law. SOLUTION Remembering that voltage is energy per unit charge, we have Energy = V q Solving Equation 20.1 for q gives q = I t, which can be substituted in the previous result to give Energy = V q = VI t According to Ohm’s law (Equation 20.2), the current is I = V/R, which can be substituted in the energy expression to show that 2 2 0 V 0 s V V t 1 26 4J t E n e r g y V ItV 6 .2 1 0 R R 1 4 ______________________________________________________________________________ 8. REASONING AND SOLUTION a. The total charge that can be delivered is 3 6 0 0 s 5 q ( 2 2 0 A h ) 7 . 9 1 0 C 1 h b. The maximum current is 2 2 0 A h I 3 5 0 A h r 1 ( 3 8 m i n ) 6 0 m i n ______________________________________________________________________________ 9. REASONING The number N of protons that strike the target is equal to the amount of electric charge q striking the target divided by the charge e of a proton, N = (q)/e. From Equation 20.1, the amount of charge is equal to the product of the current I and the time t. 16 ELECTRIC CIRCUITS We can combine these two relations to find the number of protons that strike the target in 15 seconds. The heat Q that must be supplied to change the temperature of the aluminum sample of c m T, where c is the specific mass m by an amount Tis given by Equation 12.4 as Q heat capacity of aluminum. The heat is provided by the kinetic energy of the protons and is equal to the number of protons that strike the target times the kinetic energy per proton. Using this reasoning, we can find the change in temperature of the block for the 15 secondtime interval. SOLUTION a. The number N of protons that strike the target is 6 q I t( 0 . 5 0 1 0 A ) ( 1 5 s ) 1 3 N 4 . 7 1 0 1 9 ee 1 . 6 1 0 C b. The amount of heat Q provided by the kinetic energy of the protons is 1 3 1 2 Q ( 4 . 7 1 0 p r o t o n s ) ( 4 . 9 1 0 J / p r o t o n ) 2 3 0 J Since QcmT and since Table 12.2 gives the specific heat of aluminum as c = 9.00 102 J/(kg.C°), the change in temperature of the block is Q 2 3 0 J T 1 7 C c m 2J 3 9 . 0 0 1 0 ( 1 5 1 0 k g ) k g C ______________________________________________________________________________ 10. REASONING The resistance R of a wire that has a length L and a cross-sectional area A is L given by Equation 20.3 as R . Both wires have the same length and cross-sectional A area. Only the resistivity ρ of the wire differs, and Table 20.1 gives the following values: ρAluminum = 2.82 × 108 Ω·m and ρCopper = 1.72 × 108 Ω·m. Applying Equation 20.3 to both wires and dividing the two equations will allow us to eliminate the unknown length and cross-sectional area algebraically and solve for the resistance of the copper wire. SOLUTION Applying Equation 20.3 to both wires gives L L R n d R C o p p e r C o p p e r a A l u m i n u m A l u m i n u m A A Dividing these two equations, eliminating L and A algebraically, and solving the result for RCopper give Chapter 20 Problems 17 L /A C o p p e r C o p p e r R L /A A l u m i n u m A l u m i n u m A l u m i n u m R C o p p e r 8 1 . 7 2 1 0 m C o p p e r R R 0 . 2 0 0 . 1 2 C o p p e r A l u m i n u m 8 2 . 8 2 1 0 m A l u m i n u m 11. REASONING AND SOLUTION The resistance of the cable is V L R I A 2 Since A = r , the radius of the cable is 1 . 7 2 1 0 m 0 . 2 4 m 1 2 0 0 A L I r 9 . 9 1 0 m V 1 . 6 1 0 V – 8 – 3 – 2 ______________________________________________________________________________ 12. REASONING AND SOLUTION Using Equation 20.3 and the resistivity of aluminum from Table 20.1, we find 2 . 8 2 1 0 m 1 0 . 0 1 0 m L R 0 . 5 8 – 8 3 – 4 2 A 4 . 9 1 0 m ______________________________________________________________________________ 13. REASONING The resistance of a metal wire of length L, cross-sectional area A and resistivity is given by Equation 20.3: R L/ A. Solving for A, we have A L/ R. We can use this expression to find the ratio of the cross-sectional area of the aluminum wire to that of the copper wire. SOLUTION Forming the ratio of the areas and using resistivity values from Table 20.1, we have – 8 A L / R 2 . 8 2 1 0 m a l u m i n u m a l u m i n u m a l u m i n u m – 1 . 6 4 8 A L / R 1 . 7 2 1 0 m c o p p e r c o p p e r c o p p e r ______________________________________________________________________________ 18 ELECTRIC CIRCUITS 14. REASONING AND SOLUTION Solving Equation 20.5 for yields R 4 . 7 – 1 3 – 1 R 3 8 . 0 – 1 0 0 . 0 0 5 0 C T – T 5 C – 2 5 C 05 ______________________________________________________________________________ 15. REASONING AND SOLUTION First, we find from the known values of T, T0, R, and R0. We have from Equation 20.5 R 7 . 6 0 1 4 1 R 3 5 . 0 0 1 0 0 . 0 0 4 5 0 ( C ) T T 1 0 0 . 0 C 2 0 . 0 C 0 We know that R = R0[1 + (T – T0)], and using R = 37.80 we find R 3 7 . 8 0 1 1 R 3 5 . 0 0 0 T T 2 0 . 0 C 3 7 . 8 C 0 1 0 . 0 0 4 5 0 ( C ) ______________________________________________________________________________ 16. REASONING Assuming that the resistance is R at a temperature T and R0 at a temperature T0, we can write the percentage change p in resistance as R R 0 p 1 0 0 R 0 Equation 20.5, on the other hand, gives the resistance as a function of temperature as follows: RR 0 1 0 TT where α is the temperature coefficient of resistivity. Substituting this expression into the expression for the percentage change in resistance gives R R T T R R R 0 0 0 0 0 p 1 0 0 1 0 0 T T 100 0 R R 0 0 (1) The change in temperature is unknown, but it is the same for both wires. Therefore, we will apply Equation (1) to each wire and divide the two expressions to eliminate the unknown change in temperature. From the result we will be able to calculate the percentage change in the resistance of the tungsten wire. Chapter 20 Problems SOLUTION Applying Equation (1) to both wires gives 19 p T T 1 0 0 a n d p T T 1 0 0 T u n g s t e n T u n g s t e n 0 G o l d G o l d 0 Dividing these two expressions, eliminating (T T0) algebraically, and solving for pTungsten give p 0 0 0 TT 1 T u n g s t e n T u n g s t e n T u n g s t e n p 0 0 0 TT 1 G o l d G o l d G o l d 1 0 .0 0 4 5 C T u n g s t e n p p 7 .0 % 9 .3 % T u n g s t e n G o l d 1 0 .0 0 3 4 C o l d G 17. REASONING AND SOLUTION Suppose that when the initial temperature of the wire is T0 the resistance is R0, and when the temperature rises to T the resistance is R. The relation between temperature and resistance is given by Equation 20.5 as R = R0[1 + (T – T0)], where is the temperature coefficient of resistivity. The initial and final resistances are related to the voltage and current as R0 = V/I0 and R = V/I, where the voltage V across the wire is the same in both cases. Substituting these values for R0 and R into Equation 20.5 and solving for T, we arrive at 1 I0 .5 0 A 1 1 I 1 .3 0 A T T 2 0 C 3 6 0 C 0 4( 1 4 .5 1 0 C ) ______________________________________________________________________________ 18. REASONING The length L of the wire is related to its resistance R and cross-sectional area A by L AR/ (see Equation 20.3), where is the resistivity of tungsten. The resistivity is known (see Table 20.1), and the cross-sectional area can be determined since the radius of the wire is given. The resistance can be obtained from Ohm’s law as the voltage divided by the current. SOLUTION The length L of the wire is L AR (1) 20 ELECTRIC CIRCUITS 2 Since the cross-section of the wire is circular, its area is A r , where r is the radius of the wire. According to Ohm’s law (Equation 20.2), the resistance R is related to the voltage V and current I by R V / I . Substituting the expressions for A and R into Equation (1) gives 1 2 0 V V 3 2 0 . 0 0 3 0 1 0 m r A R 1 . 2 4 A I L 2 0 . 0 4 9 m 5 . 6 1 0 m ______________________________________________________________________________ 8 19. REASONING We will ignore any changes in length due to thermal expansion. Although the resistance of each section changes with temperature, the total resistance of the composite does not change with temperature. Therefore, R R R R t u n g s t e n 0 c a r b o n 0 t u n g s t e n c a r b o n t t e m p e r a t u r e T A t r o o m t e m p e r a t u r e A From Equation 20.5, we know that the temperature dependence of the resistance for a wire R [ 1 ( T T ) ], where is the 0 0 0 is given by R 0 at temperature T of resistance R temperature coefficient of resistivity. Thus, R R R ( 1 T ) R ( 1 T ) t u n g s t e n c a r b o n t u n g s t e n u n g s t e n 0 0 0t c a r b o n a r b o n 0c Since Tis the same for each wire, this simplifies to R – R t u n g s t e n u n g s t e n 0t c a r b o n a r b o n 0c (1) This expression can be used to find the ratio of the resistances. Once this ratio is known, we can find the ratio of the lengths of the sections with the aid of Equation 20.3 (L = RA/). SOLUTION From Equation (1), the ratio of the resistances of the two sections of the wire is – 1 R t u n g s t e n – 0 . 0 0 0 5 [ ( C ) ]1 0 c a r b o n – – – 1 9 R 0 . 0 0 4 5 [ ( C ) ] t u n g s t e n c a r b o n 0 Thus, using Equation 20.3, we find the ratio of the tungsten and carbon lengths to be – 5 R R A / L u n g s t e n 1 3 . 5 1 0 m t u n g s t e n0 t u n g s t e nt 0 c a r b o n 7 0 – 8 L 9 R A / R 5 . 6 1 0 m c a r b o n t u n g s t e n 0 c a r b o n c a r b o n 0 Chapter 20 Problems 21 where we have used resistivity values from Table 20.1 and the fact that the two sections have the same cross-sectional areas. ______________________________________________________________________________ 20. REASONING AND SOLUTION The resistance of the thermistor decreases by 15% relative to its normal value of 37.0 °C. That is, R RR 0 0 .1 5 R R 0 0 According to Equation 20.5, we have R = R0[1 + (T – T0)] or (R – R0) = R0(T – T0) or R R 0 T T 0 . 1 5 0 R 0 Rearranging this result gives 0 . 1 5 0 . 1 5 T T 3 7 . 0 C 3 9 . 5 ° C 0 1 0 . 0 6 0 C ______________________________________________________________________________ 21. REASONING AND SOLUTION According to Equation 20.6c, the power delivered to the iron is 2 2 0V V 1 2 2W P 6 .0 1 0 R 2 4 ______________________________________________________________________________ 22. REASONING To find the current, we can use the relation that the power P is the product of the current I and the voltage V, since the power and voltage are known. SOLUTION Solving P I V (Equation 20.6a) for the current, we have P0 . 1 1 W I 0 . 0 2 4 A V4 . 5 V ______________________________________________________________________________ 23. REASONING AND SOLUTION The power delivered is P = VI so a. Pbd = VIbd = (120 V)(11 A) = 1300 W b. Pvc = VIvc = (120 V)(4.0 A) = 480 W c. The energy is E = Pt so, 22 ELECTRIC CIRCUITS E t 1 3 0 0 W ) ( 1 5 m i n ) b dP b d b d( 1 . 4 E t 4 8 0 W ) ( 3 0 . 0 m i n ) v cP v c v c( ______________________________________________________________________________ 24. REASONING The total cost of keeping all the TVs turned on is equal to the number of TVs times the cost to keep each one on. The cost for one TV is equal to the energy it consumes times the cost per unit of energy ($0.12 per kWh). The energy that a single set uses is, according to Equation 6.10b, the power it consumes times the time of use. SOLUTION The total cost is T o t a l c o s t = 1 1 0 m i l l i o n s e t s C o s t p e r s e t $ 0 . 1 2 1 1 0 m i l l i o n s e t s E n e r g y i n k W h u s e d p e r s e t 1 k W h The energy (in kWh) used per set is the product of the power and the time, where the power is expressed in kilowatts and the time is in hours: 1 k W E n e r g y u s e d p e r s e t = P t 7 5 W6 . 0 h 1 0 0 0 W (6.10b) The total cost of operating the TV sets is 1 k W $ 0 . 1 2 6 T o t a l c o s t = 1 1 0 m i l l i o n s e t s 7 5 W 6 . 0 h $ 5 . 9 1 0 1 0 0 0 W 1 k W h ______________________________________________________________________________ 25. REASONING According to Equation 6.10b, the energy used is Energy = Pt, where P is the power and t is the time. According to Equation 20.6a, the power is P = IV, where I is the current and V is the voltage. Thus, Energy = IVt, and we apply this result first to the dryer and then to the computer. SOLUTION The energy used by the dryer is 0 s 6 7 E n e r g y P tI V t( 1 6 A ) ( 2 4 0 V ) ( 4 5 m in ) 1 .0 4 1 0 J .0 0 m in 11 4 2 4 3 C o n v e r tsm in u te s to s e c o n d s For the computer, we have 7J E n e r g y 1 .0 4 1 0 I V t2 .7 A 1 2 0 V t Chapter 20 Problems 23 Solving for t we find 7 1 . 0 4 1 0 J 1 . 0 0 h 4 4 t 3 . 2 1 1 0 s 3 . 2 1 1 0 s 8 . 9 h 2 . 7 A 1 2 0 V 3 6 0 0 s ______________________________________________________________________________ 26. REASONING AND SOLUTION We know that the resistance of the wire can be obtained from P = V 2 /R or R = V 2 /P We also know that R = L/A. Solving for the length, noting that A = r2, and using = 100 10–8 .m from Table 20.1, we find 2 2 22 – 4 2 V / P r 1 2 0 V . 5 1 0 m 6 R A V r L 5 0 m – 8 2 P 1 0 0 1 0 m 4 . 0 0 1 0 W 2 ______________________________________________________________________________ 27. REASONING AND SOLUTION As a function of temperature, the resistance of the wire 0 1 ( TT 0) is given by Equation 20.5: RR , where is the temperature coefficient of 2 V/R resistivity. From Equation 20.6c, we have P . Combining these two equations, we have 2 P V P 0 T – T 1 R 1 T – T 0 0 0 1 2P 0, so we find where P0 = V2/R0, since the voltage is constant. But P P P 0 0 o r 2 1 T T 0 2 1 T – T 0 Solving for T, we find 1 1 T T 2 8 2 5 0 C 0 – 1 0 . 0 0 4 5 ( C ) ______________________________________________________________________________ 28. REASONING A certain amount of time t is needed for the heater to deliver the heat Q required to raise the temperature of the water, and this time depends on the power produced by the heater. The power P is the energy (heat in this case) per unit time, so the time is the heat divided by the power or t = Q/P. The heat required to raise the temperature of a mass m 24 ELECTRIC CIRCUITS of water by an amount T is given by Equation 12.4 as Q = cmT, where c is the specific heat capacity of water [4186 J/(kg·Cº), see Table 12.2]. The power dissipated in a resistance R is given by Equation 20.6c as PV2 / R, where V is the voltage across the resistor. Using these expressions for Q and P will allow us to determine the time t. SOLUTION Substituting Equations 12.4 and 20.6c into the expression for the time and recognizing that the normal boiling point of water is 100.0 ºC, we find that Q c m TR c m T t2 2 PV /R V 1 5 4 1 8 6 J /k C0 5 0 k g 1 0 0 . 0 C 1 3 C g . 1 9 0 s 2 1 2 0 V 29. REASONING AND SOLUTION The electrical energy is converted to heat, so we have Q c m Tc m T T 0 This energy is also given by 2 2 1 Q P tI R tI R R t a v 0 2 where we are considering the average resistance Rav over the one minute interval. Also RR 0 1 0 TT We have 2 2 1 1 Q IR t I R 2 T T t c m T T R 0 0 0 0 2 2 Solving for T in the expression above yields R0I2t cm T T0 R I2t 1 0 2cm Using R0 = 12 , I = 0.10 A, t = 60.0 s, m = 1.3 10–3 kg, c = 452 J/(kg.C°) from Table 12.2, = 0.0050 (C°)–1, T0 = 20.0 °C, we obtain T 33°C . ______________________________________________________________________________ Chapter 20 Problems 25 1 30. REASONING Substituting V 2 V0 into Equation 20.7 gives a result that can be solved directly for the desired time. SOLUTION From Equation 20.7 we have 1 V V V s i n 2 f to r1 s i n 2 f t 00 2 2 Using the inverse trigonometric sine function, we find 11 2 ft s i n 0 . 5 2 4 2 In this result, the value of 0.524 is in radians and corresponds to an angle of 30.0º. Thus we find that the smallest value of t is 0 . 5 2 4 0 . 5 2 4 3 t 1 . 3 9 1 0 s 2 f 2 6 0 . 0 H z 31. REASONING AND SOLUTION The expression relating the peak current, I0, to the rmscurrent, Irms, is I . 5 0 A 0 2 I 1 . 7 7 A r m s 2 2 ______________________________________________________________________________ 32. REASONING a. The average power P delivered to the copy machine is equal to the square of the 2 rms-current Irms times the resistance R, or P Irms R (Equation 20.15b). Both Irms and R are known. b. According to the discussion in Section 20.5, the peak power Ppeak is twice the average power, or Ppeak 2P. SOLUTION a. The average power is 2 P IR 6 . 5 0 A 1 8 . 6 7 8 6 W r m s 2 b. The peak power is twice the average power, so (20.15b) 26 ELECTRIC CIRCUITS P 22 P 7 8 6 W 1 5 7 2 W p e a k ______________________________________________________________________________ 33. 2 /R V SSM REASONING The average power is given by Equation 20.15c as P . In rm s this expression the rms voltage Vrms appears. However, we seek the peak voltage V0. The rm sV 0/ 2 relation between the two types of voltage is given by Equation 20.13 as V , so we can obtain the peak voltage by using Equation 20.13 to substitute into Equation 20.15c. SOLUTION Substituting Vrms from Equation 20.13 into Equation 20.15c gives 2 V /2 V V 0 s P rm 0 R R 2 R 2 2 Solving for the peak voltage V0 gives VR 2 P 2 4 . 0 5 5 W 2 1 V 0 ______________________________________________________________________________ 34. REASONING AND SOLUTION The power P dissipated in the extension cord is P = I 2 R (Equation 20.6b). The resistance R is related to the length L of the wire and its crosssectional area A by Equation 20.3, R = L/A, where is the resistivity of copper. The crosssectional area of the wire can be expressed as A L I2 R P L where the ratio P/L is the power per unit length of copper wire that the heater produces. The wire is cylindrical, so its cross-sectional area is A = r2 . Thus, the smallest radius of wire that can be used is 8 1 . 7 2 1 0 m 3 r I ( 1 8 A ) 1 . 3 1 0 m P ( 1 . 0 W / m ) L Note that we have used 1.0 W/m as the power per unit length, rather than 2.0 W/m. This is because an extension cord is composed of two copper wires. If the maximum power per unit length that the extension cord itself can produce is 2.0 W/m, then each wire can produce only a maximum of 1.0 W/m. ______________________________________________________________________________ Chapter 20 Problems 27 35. REASONING AND SOLUTION The total amount of energy needed is 9 h 3 6 0 0 s 9 2 2 E P t I R t ( 2 5 A ) ( 5 . 3 ) ( 3 1 d ) 3 . 3 1 0 J 1 d 1 h To find the cost, then, $ 0 . 1 2 1 k W h 9 C o s t 3 . 3 1 0 J $ 1 1 0 6 1 k W h 3 . 6 1 0 J ______________________________________________________________________________ 36. REASONING a. We can obtain the frequency of the alternating current by comparing this specific expression for the current with the more general one in Equation 20.8. b. The resistance of the light bulb is, according to Equation 20.14, equal to the rms-voltage divided by the rms-current. The rms-voltage is given, and we can obtain the rms-current by dividing the peak current by 2 , as expressed by Equation 20.12. c. The average power is given by Equation 20.15a as the product of the rms-current and the rms-voltage. SOLUTION 0 . 7 0 7 A s i n 3 1 4 H z t a. By comparing I with the general expression (see Equation 20.8) for the current in an ac circuit, II0sin2ft, we see that 3 1 4 H z 2 f t 3 1 4 H zo t rf = 5 0 . 0 H z 2 b. The resistance is equal to Vrms/Irms, where the rms-current is related to the peak current I0 by Irms I0 / 2. Thus, the resistance of the light bulb is V 1 2 0 . 0 V 2 r m sV r m s 2 R 2 . 4 0 1 0 I I 0 . 7 0 7 A r m s 0 2 (20.14) c. The average power is the product of the rms-current and rms-voltage: I 0 . 7 0 7 A 0 P I V V 1 2 0 . 0 V 6 0 . 0 W(20.15a) r m s r m s r m s 2 2 ______________________________________________________________________________ 28 ELECTRIC CIRCUITS 37. REASONING According to Equation 6.10b, the energy supplied to the water in the form of heat is Q = Pt, where P is the power and t is the time. According to Equation 20.6c, the power is P = V 2 /R, so that Q = (V 2 /R)t, where V is the voltage and R is the resistance. But for a mass m of water with a specific heat capacity c, the heat Q is related to the change in temperature T by Q = mcT according to Equation 12.4. Our solution uses these two expressions for Q. SOLUTION Combining the two expressions for Q, we have Q = mcT = V 2 t/R. Solving for t, we have R c m T t (1) 2 V w a te r . From Equation 11.1, we The mass of the water can be determined from its volume V 3 3 1 . 0 0 0 1 0 k g / m have m is the mass density of water (see w aterV w ater, where w a t e r Table 11.1). Therefore, Equation (1) becomes R c aterV T w a t e r t w 2 V (2) . The value (see Table 12.2) for the specific heat of water is 4186 J/(kg C°). The volume of water is – 3 3 3 .7 9 1 0 m 3 V 5 2 g a l .1 9 7 m 0 w a te r .0 0 g a l 1 Substituting values into Equation (2), we obtain 3 3 3 ( 3 .0 ) [ 4 1 8 6 J /( k g C ) ] ( 1 .0 0 01 0 k g /m ) ( 0 .1 9 7 m ) ( 5 3C – 1 1 C ) t 7 2 2 0s 2 ( 1 2 0 V ) .0 0h 1 2 = ( 7 2 2 0 s ) .0 h 3 6 0 0 s ______________________________________________________________________________ 38. REASONING AND SOLUTION The energy Q1 that is released when the water cools from an initial temperature T to a final temperature of 0.0 °C is given by Equation 12.4 as Q1 = cm(T – 0.0 °C). The energy Q2 released when the water turns into ice at 0.0 °C is Q2 = mLf, where Lf is the latent heat of fusion for water. Since power P is energy divided by time, the power produced is Q Q m ( T 0 . 0 C ) m L 1 2c f P t t Chapter 20 Problems 29 The power produced by an electric heater is, according to Equation 20.6a, P = IV. Substituting this expression for P into the equation above and solving for the current I, we get c m ( T 0 . 0) C m L f I t V 4 ( 4 1 8 6 J / k g C ) ( 6 6 0 k g ) ( 1 0 . 0 C )( 6 6 0 k g ) ( 3 3 . 5 1 0 J / k g ) I 3 2 A 3 6 0 0 s ( 9 . 0 h ) ( 2 4 0 V ) h ______________________________________________________________________________ 39. REASONING Using Ohm's law (Equation 20.2) we can write an expression for the voltage across the original circuit as V I0R0 . When the additional resistor R is inserted in series, assuming that the battery remains the same, the voltage across the new combination is given by VI(RR 0). Since V is the same in both cases, we can write IR I(R R 0 0 0). This expression can be solved for R0 . SOLUTION Solving for R0 , we have I R – I R I R o rR ( I – I ) I R 0 0 0 0 0 Therefore, we find that I R ( 1 2 . 0 A ) ( 8 . 0 0 ) R 3 2 0 II –1 5 . 0 A – 1 2 . 0 A 0 ______________________________________________________________________________ 40. REASONING According to Equation 20.2, the resistance R of the resistor is equal to the voltage VR across it divided by the current I, or R = VR /I . Since the resistor, the lamp, and the voltage source are in series, the voltage across the resistor is VR = 120.0 V VL, where VL is the voltage across the lamp. Thus, the resistance is 1 2 0 .0VV L R I Since VL is known, we need only determine the current in the circuit. Since we know the voltage VL across the lamp and the power P dissipated by it, we can use Equation 20.6a to find the current: I P/VL . The resistance can be written as 30 ELECTRIC CIRCUITS 120.0VVL R P VL SOLUTION Substituting the known values for VL and P into the equation above, the resistance is 1 2 0 . 0 V 2 5 V 1 R 4 . 0 1 0 6 0 . 0 W 2 5 V ______________________________________________________________________________ 41. REASONING AND SOLUTION The equivalent resistance of the circuit is Rs = R1 + R2 = 36.0 + 18.0 = 54.0 Ohm's law for the circuit gives I = V/Rs = (15.0 V)/(54.0 ) = 0.278 A a. Ohm's law for R1 gives V1 = (0.278 A)(36.0 ) = b. Ohm's law for R2 gives V2 = (0.278 A)(18.0 ) = ______________________________________________________________________________ 42. REASONING Since the two resistors are connected in series, they are equivalent to a single equivalent resistance that is the sum of the two resistances, according to Equation 20.16. Ohm’s law (Equation 20.2) can be applied with this equivalent resistance to give the battery voltage. SOLUTION According to Ohm’s law, we find V I R I R R 0 . 1 2 A 4 7 2 8 9 . 0 V s 1 2 ______________________________________________________________________________ s is the sum of the resistances of 43. REASONING The equivalent series resistance R V the three resistors. The potential difference can be determined from Ohm's law as V I R s. SOLUTION a. The equivalent resistance is R 5 4 57 5 1 4 5 s 2 b. The potential difference across the three resistors is Chapter 20 Problems 31 V I R 0 .5 1 A ) ( 1 4 5 ) 7 4 V s( ______________________________________________________________________________ 44. REASONING The circuit containing the light bulb and resistor is shown in the drawing. 2 The resistance R1 of the light bulb is related to the power delivered to it by R1 P1 / I (Equation 20.6b), where I is the current in the circuit. The power is known, and the current can be obtained from Ohm’s law as the voltage V of the source divided by the equivalent resistance R of the series circuit: I V / RS. Since the two resistors are wired in series, the S equivalent resistance is the sum of the resistances, or RS R 1R 2. Light bulb R2 = 144 Ω R1 P1 = 23.4 W 120.0 V SOLUTION The resistance of the light bulb is R1 P1 (20.6b) I2 Substituting I V / RS (Equation 20.2) into Equation 20.6b gives 2 P R P P 1S 1 1 R 1 2 2 I V /R 2 V S (1) The equivalent resistance of the two resistors wired in series is RS R 1R 2 (Equation 20.16). Substituting this expression for RS into Equation (1) yields 2 P 2 P R RR 1 1 S 1 R 1 2 2 V V 2 Algebraically rearranging this equation, we find that 2 V 2 2 R 2 R R R 0 1 2 1 2 P 1 32 ELECTRIC CIRCUITS This is a quadratic equation in the variable R1. The solution can be found by using the quadratic formula (see Appendix C.4): 2 V 2 R 2 P 1 R 1 2 2 V 2 2 R 4 R 2 2 P 1 2 2 1 2 1 2 2 0 . 0 V 2 0 . 0 V 2 2 1 4 4 2 1 4 4 4 1 4 4 2 3 .4W 2 3 .4W 2 8 5 .9a n d2 4 2 ______________________________________________________________________________ 45. SSM REASONING The resistance of one of the wires in the extension cord is given by . Equation 20.3: R L/ A, where the resistivity of copper is = 1.72 108 m, according to Table 20.1. Since the two wires in the cord are in series with each other, their R R 2/ L A total resistance is R . Once we find the equivalent resistance c o r d w i r e 1 w i r e 2 of the entire circuit (extension cord + trimmer), Ohm's law can be used to find the voltage applied to the trimmer. SOLUTION a. The resistance of the extension cord is – 8 2 L 2 ( 1 . 7 2 1 0 m ) ( 4 6 m ) R 1 . 2 c o r d – 6 2 A 1 . 3 1 0 m b. The total resistance of the circuit (cord + trimmer) is, since the two are in series, R .2 1 5 .0 1 6 .2 s1 I R Therefore from Ohm's law (Equation 20.2: V ), the current in the circuit is I V 1 2 0 V 7 .4 A R 6 .2 s 1 Finally, the voltage applied to the trimmer alone is (again using Ohm's law), V 7 .4 A ) ( 1 5 .0 ) 1 1 0 V tr i m m e r ( ______________________________________________________________________________ Chapter 20 Problems 33 46. REASONING AND SOLUTION The voltage VCu between the ends of the copper rod is given by Ohm’s law as VCu = IRCu, where RCu is the resistance of the copper rod. The current I in the circuit is equal to the voltage V of the battery that is connected across the free ends of the copper-iron rod divided by the equivalent resistance of the rod. The copper and iron rods are joined end-to-end, so the same current passes through each. Thus, they are connected in series, so the equivalent resistance RS is RS = RCu + RFe. Thus, the current is V V I R R S R C u F e The voltage across the copper rod is V V I R R C u C u C u R R C u F e The resistance of the copper and iron rods is given by RCu = CuL/A and RFe = FeL/A, where the length L and cross-sectional area A is the same for both rods. Substituting these expressions for the resistances into the equation above and using resistivities from Table 20.1 yield V V r C u C u r r C u F e 1 2 V 8 V ( 1 . 7 2 1 0 m ) 1 . 8 V C u 8 8 1 . 7 2 1 0 m 9 . 7 1 0 m ______________________________________________________________________________ 47. REASONING Ohm’s law provides the basis for our solution. We will use it to express the current from the battery when both resistors are connected and when only one resistor at a time is connected. When both resistors are connected, we will use Ohm’s law with the series equivalent resistance, which is R1 + R2, according to Equation 20.16. The problem statement gives values for amounts by which the current increases when one or the other resistor is removed. Thus, we will focus attention on the difference between the currents given by Ohm’s law. SOLUTION When R2 is removed, leaving only R1 connected, the current increases by 0.20 A. In this case, using Ohm’s law to express the currents, we have 34 ELECTRIC CIRCUITS V R V V 2 – 0 .2 0 A R R R R R R 1 1 2 1 1 2 14 4244 3 1442443 C u rre n tg iv e n b y O h m 'sla w w h e n o n ly R sp re s e n t 1i C u rre n tg iv e n b y O h m 'sla w w h e n R n dR rep re s e n t 1a 2a (1) When R1 is removed, leaving only R2 connected, the current increases by 0.10 A. In this case, using Ohm’s law to express the currents, we have V R V V 1 – 0 .1 0 A R R R R R R 2 1 2 2 1 2 14 4244 3 1442443 C u rre n tg iv e n b y O h m 'sla w w h e n o n ly R2isp re s e n t C u rre n tg iv e n b y O h m 'sla w w h e n R n dR rep re s e n t 1a 2a (2) Multiplying Equation (1) and Equation (2), we obtain V V R R 0 . 2 0 A 0 . 1 0 A 2 1 R R R R R R 1 12 2 12 Simplifying this result algebraically shows that 2 V V 0 . 2 0 A 0 . 1 0 A o r 0 . 2 0 A 0 . 1 0 A 0 . 1 4 A (3) 2 R R R R 1 2 1 2 a. Using the result for V/(R1 + R2) from Equation (3) to substitute into Equation (1) gives V V 1 2 V – 0 . 1 4 A = 0 . 2 0 A o r R 3 5 1 R 0 . 2 0 A + 0 . 1 4 A 0 . 2 0 A + 0 . 1 4 A 1 b. Using the result for V/(R1 + R2) from Equation (3) to substitute into Equation (2) gives V V1 2 V1 – 0 . 1 4 A = 0 . 1 0 A o r R 5 . 0 1 0 2 R 0 . 1 0 A + 0 . 1 4 A 0 . 1 0 A + 0 . 1 4 A 2 ______________________________________________________________________________ 48. REASONING AND SOLUTION The rule for combining parallel resistors is 1 1 1 R P R 1 R 2 which gives Chapter 20 Problems 35 1 1 1 1 1 o r R 4 6 24 R 1 5 1 5 5 2 R P R 1 1 ______________________________________________________________________________ 49. REASONING AND SOLUTION Since the circuit elements are in parallel, the equivalent resistance can be obtained directly from Equation 20.17: 1 1 1 1 1 R 6 8 .0 p R 1 R 2 1 o r R .3 p5 ______________________________________________________________________________ 50. REASONING AND SOLUTION The power P dissipated in a resistance R is given by Equation 20.6c as P = V 2 /R. The resistance R50 of the 50.0-Wfilament is 2 ( V 1 2 0 .0 V )2 R 2 8 8 5 0 P 5 0 .0 W The resistance R100 of the 100.0-W filament is 2 ( V 1 2 0 .0 V )2 1 4 4 P 1 0 0 .0 W ______________________________________________________________________________ R 1 0 0 51. REASONING The total power is given by Equation 20.15c as P Vrms / Rp , where Rp is the equivalent parallel resistance of the heater and the lamp. Since the total power and the rms voltage are known, we can use this expression to obtain the equivalent parallel resistance. This equivalent resistance is related to the individual resistances of the heater and the lamp 2 via Equation 20.17, which is once Rp is known. –1 –1 R p–1 R heater Rlamp . Since Rheater is given, Rlamp can be found SOLUTION According to Equation 20.15c, the equivalent parallel resistance is Rp 2 Vrms P Using this result in Equation 20.17 gives 1 1 1 1 2 Rp Rheater R lamp Vrms / P Rearranging this expression shows that 36 ELECTRIC CIRCUITS 1 P 1 1 1 1 W 1 – 3 – 1 –2 –2 5 . 2 1 0 2 R R V 4 . 0 1 0 1 2 0 V l a m p e a t e r r m sh Therefore, 1 R 1 9 0 l a m p – 3– 1 5 . 2 1 0 52. REASONING When the switch is open, no current goes to the resistor R2. Current exists only in R1, so it is the equivalent resistance. When the switch is closed, current is sent to both resistors. Since they are wired in parallel, we can use Equation 20.17 to find the equivalent resistance. Whether the switch is open or closed, the power P delivered to the circuit can be found from the relation PV2 / R (Equation 20.6c), where V is the battery voltage and R is the equivalent resistance. SOLUTION a. When the switch is open, there is current only in resistor R1. Thus, the equivalent resistance is R 1 65.0. b. When the switch is closed, there is current in both resistors and, furthermore, they are wired in parallel. The equivalent resistance is 1 1 11 1 o r R 3 8 . 8 (20.17) P R R R 6 5 . 0 9 6 . 0 P 1 2 c. When the switch is open, the power delivered to the circuit by the battery is given by PV2 / R1, since the only resistance in the circuit is R1. Thus, the power is 2 V 9 . 0 0 V P 1 . 2 5 W R 6 5 . 0 1 2 (20.6) 2 d. When the switch is closed, the power delivered to the circuit is PV / RP, where RP is the equivalent resistance of the two resistors wired in parallel: 2 V 9 . 0 0 V P 2 . 0 9 W (20.6) R 8 . 8 P 3 ______________________________________________________________________________ 2 Chapter 20 Problems 37 53. REASONING Since the resistors are connected in parallel, the voltage across each one is I R the same and can be calculated from Ohm's Law (Equation 20.2: V ). Once the voltage across each resistor is known, Ohm's law can again be used to find the current in the second resistor. The total power consumed by the parallel combination can be found calculating the power consumed by each resistor from Equation 20.6b: P = I 2 R. Then, the total power consumed is the sum of the power consumed by each resistor. SOLUTION Using data for the second resistor, the voltage across the resistors is equal to V I R ( 3 . 0 0 A ) ( 6 4 . 0 ) = 1 9 2 V a. The current through the 42.0- resistor is I V1 9 2 V 4 .5 7 A R4 2 .0 b. The power consumed by the 42.0- resistor is P I2R (4 .5 7 A )2(4 2 .0)=8 7 7 W while the power consumed by the 64.0- resistor is P I2R (3 .0 0 A )2(6 4 .0 )=5 7 6 W 7 7 W + 5 7 6 W =1 4 5 0 W Therefore the total power consumed by the two resistors is 8 . ______________________________________________________________________________ 54. REASONING AND SOLUTION Each piece has a resistance of 1R 3 . Then 1111 9 1 o rR R p 9 1 1 1 R R R R R p3 3 3 ______________________________________________________________________________ p 55. REASONING The equivalent resistance of the three devices in parallel is R , and we can R find the value of pby using our knowledge of the total power consumption of the circuit; 2 V /R pcan be found from Equation 20.6c, P the value of R . Ohm's law (Equation 20.2, p V I R ) can then be used to find the current through the circuit. SOLUTION a. The total power used by the circuit is P = 1650 W + 1090 W +1250 W = 3990 W. The equivalent resistance of the circuit is 38 ELECTRIC CIRCUITS 2 ( V 1 2 0 V )2 R 3 .6 p P 3 9 9 0 W b. The total current through the circuit is I V 1 2 0 V 3 3 A R .6 p 3 r e a k e rw i l lo p e n. This current is larger than the rating of the circuit breaker; therefore, the b ______________________________________________________________________________ 56. REASONING AND SOLUTION The aluminum and copper portions may be viewed a being connected in parallel since the same voltage appears across them. Using a and b to denote the inner and outer radii, respectively, and using Equation 20.3 to express the resistance for each portion, we find for the equivalent resistance that 2 2 2 ba 1 1 1 A a C u A A l RRR LA LC L A L p A l C u C u l u l 3 2 3 2 3 2 3 . 0 0 1 0 m2 . 0 0 1 0 m 2 . 0 0 1 0m 0 . 0 0 1 1 6 8 8 1 . 7 2 1 0 m 1 . 5 0 m 2 . 8 2 1 0 m 1 . 5 0 m We have taken resistivity values for copper and aluminum from Table 20.1 ______________________________________________________________________________ 57. REASONING Since the defogger wires are connected in parallel, the total resistance of all thirteen wires can be obtained from Equation 20.17: 1 1 3 R p R R R p 1 3 o r where R is the individual resistance of one of the wires. The heat required to melt the ice is m L f, where m is the mass of the ice and L f is the latent heat of fusion of the given by Q ice (see Section 12.8). Therefore, using Equation 20.6c, we can see that the power or energy dissipated per unit time in the wires and used to melt the ice is 2 V m L f P R t43 p 1 42 E n e r g y /ti m e o r 2 m V L f R /1 3 t Chapter 20 Problems 39 According to Equation 20.3, R L/ A, where the length of the wire is L, its crosssectional area is A and its resistivity is ; therefore, the last expression can be written 2 2 m L 1 3 V 1 3 V f R L /A t This expression can be solved for the area A. SOLUTION Solving the above expression for A, and substituting given data, and obtaining the latent heat of fusion of water from Table 12.3, we find that L m L f A 2 1 3 V t – 8 – 2 4 ( 8 8 . 0 1 0 m ) ( 1 . 3 0 m ) ( 2 . 1 0 1 0 k g ) ( 3 3 . 5 1 0 J / k g ) – 82 3 . 5 8 1 0 m 2 1 3 ( 1 2 . 0 V ) ( 1 2 0 s ) ______________________________________________________________________________ 58. REASONING We will approach this problem in parts. The resistors that are in series will be combined according to Equation 20.16, and the resistors that are in parallel will be combined according to Equation 20.17. SOLUTION The 1.00 2.00 and 3.00 resistors are in series with an equivalent resistance of Rs = 6.00 . This equivalent resistor of 6.00 Ω is in parallel with the 3.00- resistor, so 1 1 1 RP 6.00 3.00 2.00 4.00 2.00 4.00 6.00 3.00 6.00 2.00 RP 2.00 This new equivalent resistor of 2.00 Ω is in series with the 6.00 resistor, so Rs' = 8.00 . 2.00 4.00 8.00 6.00 40 ELECTRIC CIRCUITS Rs' is in parallel with the 4.00- resistor, so 2.00 1 1 1 R 8.00 4.00 2.67 P RP 2.67 Finally, Rp' is in series with the 2.00-, so the total equivalent resistance is 4.67 Ω . ______________________________________________________________________________ 59. SSM REASONING To find the current, we will use Ohm’s law, together with the proper equivalent resistance. The coffee maker and frying pan are in series, so their equivalent resistance is given by Equation 20.16 as Rcoffee + Rpan. This total resistance is in parallel with the resistance of the bread maker, so the equivalent resistance of the parallel – 1 R – 1 – 1 combination can be obtained from Equation 20.17 as R . p ( c o f f e e R p a n) R b re a d SOLUTION Using Ohm’s law and the expression developed above for Rp–1, we find I V 1 1 1 1 V 1 2 0V .2A 9 R 1 4 1 6 2 3 p R c o f f e e R p a n R b re a d ______________________________________________________________________________ 60. REASONING The two resistors R1 and R2 are wired in series, so we can determine their equivalent resistance R12. The resistor R3 is wired in parallel with the equivalent resistance R12, so the equivalent resistance R123 can be found. Finally, the resistor R4 is wired in series with the equivalent resistance R123. With these observations, we can evaluate the equivalent resistance between the points A and B. R1 = 16 A R2 = 8 Ω R4 = 26 1 1 R3 = 48 1 B 41 Chapter 20 Problems SOLUTION Since R1 and R2 are wired in series, the equivalent resistance R12 is R R R 1 6 8 2 4 1 2 1 2 (20.16) The resistor R3 is wired in parallel with the equivalent resistor R12, so the equivalent resistance R123 of this combination is 1 1 111 o r R 1 6 2 3 R R R 4 8 2 4 1 1 2 3 3 1 2 (20.17) The resistance R4 is in series with the equivalent resistance R123, so the equivalent resistance RAB between the points A and B is R R R 2 6 1 6 4 2 A B 41 2 3 ______________________________________________________________________________ 61. REASONING When two or more resistors are in series, the equivalent resistance is given R ... . Likewise, when resistors are in parallel, the sR 1 2R 3 by Equation 20.16: R expression to be solved to find the equivalent resistance is given by Equation 20.17: 1 1 1 1 .... We will successively apply these to the individual resistors in the R p R 1 R 2 R 3 figure in the text beginning with the resistors on the right side of the figure. SOLUTION Since the 4.0- and the 6.0- resistors are in series, the equivalent resistance of the combination of those two resistors is 10.0 . The 9.0- and 8.0- resistors are in parallel; their equivalent resistance is 4.24 . The equivalent resistances of the parallel combination (9.0 and 8.0 ) and the series combination (4.0 and the 6.0 ) are in parallel; therefore, their equivalent resistance is 2.98 . The 2.98- combination is in series with the 3.0- resistor, so that equivalent resistance is 5.98 . Finally, the 5.98- combination and the 20.0- resistor are in parallel, so the equivalent resistance between the points A and B is 4.6 . ______________________________________________________________________________ 62. REASONING The circuit diagram is shown at the right. We can find the current in the 120.0- resistor by using Ohm’s law, provided that we can obtain a value for VAB, the voltage between points A and B in the diagram. To find VAB, we will also apply Ohm’s law, this time by multiplying the current from the battery times RAB, the equivalent parallel resistance between A and B. The current from the battery can be obtained by 60.0 20.0 A B 120.0 15.0 V 42 ELECTRIC CIRCUITS applying Ohm’s law again, now to the entire circuit and using the total equivalent resistance of the series combination of the 20.0- resistor and RAB. Once the current in the 120.0- resistor is found, the power delivered to it can be obtained from Equation 20.6b, P = I 2 R. SOLUTION a. According to Ohm’s law, the current in the 120.0- resistor is I120 = VAB/(120.0 ). To find VAB, we note that the equivalent parallel resistance between points A and B can be obtained from Equation 20.17 as follows: 11 1 o r R 4 0 . 0 A B R 6 0 . 0 1 2 0 . 0 A B This resistance of 40.0 is in series with the 20.0- resistance, so that, according to Equation 20.16, the total equivalent resistance connected across the battery is 40.0 + 20.0 = 60.0 . Applying Ohm’s law to the entire circuit, we can see that the current from the battery is 1 5 .0V I 0 .2 5 0 A 6 0 .0 Again applying Ohm’s law, this time to the resistance RAB, we find that V 0 . 2 5 0 A R 0 . 2 5 0 A 4 0 . 0 1 0 . 0 V A B A B Finally, we can see that the current in the 120.0- resistor is V 0 . 0 V – 2 A B1 I 8 . 3 3 1 0 A 1 2 0 1 2 0 1 2 0 b. The power delivered to the 120.0- resistor is given by Equation 20.6b as P I R 8 . 3 3 1 0 A 1 2 0 . 0 0 . 8 3 3 W 1 2 0 2 2 – 2 ______________________________________________________________________________ 63. REASONING The power P delivered to the circuit is, according to Equation 20.6c, 2 PV /R 12345, where V is the voltage of the battery and R12345 is the equivalent resistance of the five-resistor circuit. The voltage and power are known, so that the equivalent resistance can be calculated. We will use our knowledge of resistors wired in series and parallel to evaluate R12345 in terms of the resistance R of each resistor. In this manner we will find the value for R. Chapter 20 Problems 43 SOLUTION First we note that all the resistors are equal, so R1 = R2 = R3 = R4 = R5 = R. We can find the equivalent resistance R12345 as follows. The resistors R3 and R4 are in series, so the equivalent resistance R34 of these two is R34 = R3 + R4 = 2R. The resistors R2, R34, and R5 are in parallel, and the reciprocal of the equivalent resistance R2345 is 1 1 1 1111 5 R R R R R 2 R R 2 R 2 3 4 5 2 3 4 5 so R2345 = 2R/5. The resistor R1 is in series with R2345, and the equivalent resistance of this combination is the equivalent resistance of the circuit. Thus, we have 2 R 7 R R R R R 1 2 3 4 5 1 2 3 4 5 55 The power delivered to the circuit is 2 2 V V P R 7R 12345 5 Solving for the resistance R, we find that 4 5 V 5 V5 R 2 5 7 P7 5 8 W ______________________________________________________________________________ 2 2 64. REASONING The power P dissipated in each resistance R is given by Equation 20.6b as P I 2R , where I is the current. This means that we need to determine the current in each resistor in order to calculate the power. The current in R1 is the same as the current in the equivalent resistance for the circuit. Since R2 and R3 are in parallel and equal, the current in R1 splits into two equal parts at the junction A in the circuit. SOLUTION To determine the equivalent resistance of the circuit, we note that the parallel combination of R2 and R3 is in series with R1. The equivalent resistance of the parallel combination can be obtained from Equation 20.17 as follows: 11 1 o rR 2 8 8 R 5 7 6 5 7 6 P P This 288-Ω resistance is in series with R1, so that the equivalent resistance of the circuit is given by Equation 20.16 as R 5 7 6 2 8 8 8 6 4 e q 44 ELECTRIC CIRCUITS To find the current from the battery we use Ohm’s law: V1 2 0 . 0 V I 0 . 1 3 9 A R 6 4 e q 8 Since this is the current in R1, Equation 20.6b gives the power dissipated in R1 as 2 P I R 0 . 1 3 9 A 5 7 6 1 1 . 1 W 1 1 1 2 R2 and R3 are in parallel and equal, so that the current in R1 splits into two equal parts at the 1 junction A. As a result, there is a current of 20.139A in R2 and in R3. Again using Equation 20.6b, we find that the power dissipated in each of these two resistors is 2 10 PIR 3 9 A 5 7 6 2 . 7 8 W .1 2 22 2 2 2 10 PIR 3 9 A 5 7 6 2 . 7 8 W .1 3 33 2 2 65. REASONING Since we know that the current in the 8.00- resistor is 0.500 A, we can use Ohm's law (V = IR) to find the voltage across the 8.00- resistor. The 8.00- resistor and the 16.0- resistor are in parallel; therefore, the voltages across them are equal. Thus, we can also use Ohm's law to find the current through the 16.0- resistor. The currents that flow through the 8.00- and the 16.0- resistors combine to give the total current that flows through the 20.0- resistor. Similar reasoning can be used to find the current through the 9.00- resistor. SOLUTION 0 .5 0 0 A ) ( 8 .0 0 )4 .0 0 V 8( a. The voltage across the 8.00- resistor is V . Since this is also the voltage that is across the 16.0- resistor, we find that the current through the 4 .0 0 V ) / ( 1 6 .0 )0 .2 5 0 A 1 6( 16.0- resistor is I . Therefore, the total current that flows through the 20.0- resistor is I .5 0 0 A + 0 .2 5 0 A =0 .7 5 0 A 2 00 b. The 8.00- and the 16.0- resistors are in parallel, so their equivalent resistance can be 1 1 1 1 ... obtained from Equation 20.17, R , and is equal to 5.33 . Therefore, p R 1 R 2 R 3 the equivalent resistance of the upper branch of the circuit is R 5 . 3 3 + 2 0 . 0 2 5 . 3 u p p e r , since the 5.33- resistance is in series with the 20.0- Chapter 20 Problems 45 resistance. Using Ohm's law, we find that the voltage across the upper branch must be V ( 0 .7 5 0 A ) ( 2 5 .3 )= 1 9 .0 V . Since the lower branch is in parallel with the upper branch, the voltage across both branches must be the same. Therefore, the current through the 9.00- resistor is, from Ohm's law, V 9 . 0 V l o w e r 1 I 2 . 1 1 A 9 R 9 . 0 0 9 ______________________________________________________________________________ 66. REASONING AND SOLUTION The equivalent resistance of the initial configuration is given by 1 3 Rp 13 R or Rp R The parallel part of the final configuration has a resistance of Rp 2 R , so the total equivalent resistance is 1R R R 3 R s 2 2 1 Now Rs = Rp + 700 , so it follows that 3R 1R 7 0 0 2 3 or R = 600 ______________________________________________________________________________ E m f–Ir, where r 67. REASONING The terminal voltage of the battery is given by V te rm in a l is the internal resistance of the battery. Since the terminal voltage is observed to be one-half E m f/2and I E m f/2r. From Ohm's law, of the emf of the battery, we have V te rm in a l e m f/I2 r . We can also find the equivalent the equivalent resistance of the circuit is R resistance of the circuit by considering that the identical bulbs are in parallel across the battery terminals, so that the equivalent resistance of the N bulbs is found from 1 N R p R b u lb o r R p R b u lb N This equivalent resistance is in series with the battery, so we find that the equivalent resistance of the circuit is R R 2 r bulbr N This expression can be solved for N. SOLUTION Solving the above expression for N, we have 46 ELECTRIC CIRCUITS R R 1 5 N bulb bulb 3 0 2 rr r 0 .5 0 ______________________________________________________________________________ 68. REASONING When the terminal voltage of the battery (emf = 9.00 V) is 8.90 V, the voltage drop across the internal resistance r is 9.00 V 8.90 V = 0.10 V. According to Ohm’s law, this voltage drop is the current I times the internal resistance. Thus, Ohm’s law will allow us to calculate the current. SOLUTION Using Ohm’s law we find that V0 . 1 0 V I 8 . 3 A r 0 . 0 1 2 69. REASONING AND SOLUTION Ohm’s law gives V1 . 5 V r 0 . 0 5 4 I 2 8 A ______________________________________________________________________________ 70. REASONING The drawing shows the battery (emf = ), its internal resistance r, and the light bulb (represented as a resistor). The voltage between the terminals of the battery is the voltage VAB between the points A and B in the drawing. This voltage is not equal to the emf of the battery, because part of the emf is needed to make the current I go through the internal resistance. Ohm’s law states that this part of the emf is I r. The current can be determined from the relation P = I VAB, since the power P delivered to the light bulb and the voltage VAB across it are known. Light bulb 1 I A + r = 0.10 + B SOLUTION The terminal voltage 1VAB is equal to the emf of the battery minus the voltage across the internal resistance r, which is I r (Equation 20.2): VAB = I r. Solving this equation for the emf gives VABIr (1) Chapter 20 Problems 47 The current also goes through the light bulb, and it is related to the power P delivered to the bulb and the voltage VAB according to I = P/VAB (Equation 20.6a). Substituting this expression for the current into Equation (1) gives P V Ir V r A B A B A B V 4 W 2 0 1 1 .8 V .1 0 1 2 .0 V 1 1 .8 V ______________________________________________________________________________ 71. REASONING According to the discussion in Section 20.9, the emf of a battery is equal to its terminal voltage V plus the voltage Vr across the internal resistance; Emf = V + Vr . According to Equation 20.6a, however, the voltage across the internal resistance is related to the current I and the power P dissipated by the internal resistance as Vr = P/ I. Thus, the emf of the battery can be expressed as P Em f =V I SOLUTION Using the result found above, the emf of the battery is 3 4 . 0 W P E m f = V 2 3 . 4 V 2 4 . 0 V I 5 5 . 0 A ______________________________________________________________________________ 72. REASONING AND SOLUTION The power dissipated in the resistor if the battery has no internal resistance is P0 = I02R where I0 = V/R, so P0 V2 R (1) The power dissipated if the battery has an internal resistance is P = I2R, where I = V/(R + r) and P = 0.900 P0. Thus, 2 V R 0 .9 0 0 P 0 2 ( R r ) Division of Equation (2) by Equation (1) gives (2) 48 ELECTRIC CIRCUITS 2 R R r 0 .9 4 9 0 .9 0 0 0.054 or or 2 (Rr) R (Rr) ______________________________________________________________________________ 73. REASONING AND SOLUTION Apply the loop rule to get (with the units suppressed) 9.0 V = I ( 0.015 ) + I ( 0.015 ) + 8.0 V Solving this equation for the current gives I = . ______________________________________________________________________________ 74. REASONING AND SOLUTION Label the currents with the resistor values. Take I3 to the right, I2 to the left and I1 to the right. Applying the loop rule to the top loop (suppressing the units) gives I1 + 2.0 I2 = 1.0 (1) and to the bottom loop gives 2.0 I2 + 3.0 I3 = 5.0 (2) Applying the junction rule to the left junction gives I2 = I1 + I3 (3) Solving Equations (1) , (2) and (3) simultaneously, we find I2 = . The positive sign shows that the assumed direction is correct. That is, to the . ______________________________________________________________________________ 75. REASONING The current I can be found by using Kirchhoff's loop rule. Once the current is known, the voltage between points A and B can be determined. SOLUTION a. We assume that the current is directed clockwise around the circuit. Starting at the upper-left corner and going clockwise around the circuit, we set the potential drops equal to the potential rises: ( 5 . 0 ) I ( 7 I 1 0 .0 V ( 1 2 ) I4 ( 8 .0 ) I 3 0 .0 V 1 4 4 4 42 4 4) 4 4 4 2 4 4 4 4 4 4 4 4 3 1 2 3 P o te n ti a ld r o p s .3 8 A. Solving for the current gives I0 b. The voltage between points A and B is P o te n ti a lr i s e s Chapter 20 Problems 49 1V V 0 .0 V – ( 0 .3 8 A ) ( 2 7) 2 .0 1 0 A B3 o i n tB is at the higher potential. c. P ______________________________________________________________________________ 76. REASONING This problem can be solved by using Kirchhoff’s loop rule. We begin by drawing a current through each resistor. The drawing shows the directions chosen for the currents. The directions are arbitrary, and if any one of them is incorrect, then the analysis will show that the corresponding value for the current is negative. R1 = 8.0 + V1 = 4.0 V A + R2 = 2.0 + F I1 I2 V2 = 12 V + E B C D We mark the two ends of each resistor with plus and minus signs that serve as an aid in identifying the potential drops and rises for the loop rule, recalling that conventional current is always directed from a higher potential (+) toward a lower potential (–). Thus, given the directions chosen for I1 and I2 , the plus and minus signs must be those shown in the drawing. We then apply Kirchhoff's loop rule to the top loop (ABCF) and to the bottom loop (FCDE) to determine values for the currents I1 and I2. SOLUTION Applying Kirchhoff’s loop rule to the top loop (ABCF) gives V IR 1 2 2 IR 11 P o te n tia l ris e s P o te n tia l d ro p (1) Similarly, for the bottom loop (FCDE), V 2 I2R 2 Potential rise Potential drop Solving Equation (2) for I2 gives V 2 V 2 1 I 6 . 0 A 2 R . 0 2 2 (2) 50 ELECTRIC CIRCUITS Since I2 is a positive number, the current in the resistor R2 goes from left toright , as shown in the drawing. Solving Equation (1) for I1 and substituting I2 = V2/R2 into the resulting expression yields V 2 V R 1 2 R V I R V V 4 . 0 V 1 2 V 2 12 2 1 2 I 2 . 0 A 1 R R R 8 . 0 1 1 1 Since I1 is a positive number, the current in the resistor R1 goes from left toright , as shown in the drawing. ______________________________________________________________________________ 77. REASONING We begin by labeling the currents in the three resistors. The drawing below shows the directions chosen for these currents. The directions are arbitrary, and if any of them is incorrect, then the analysis will show that the corresponding value for the current is negative. We then mark the resistors with the plus and minus signs that serve as an aid in identifying the potential drops and rises for the loop rule, recalling that conventional current is always directed from a higher potential (+) toward a lower potential (–). Thus, given the directions ,I ,a n d I 1 2 3, the plus and minus signs must be those shown in the drawing. We chosen for I can now use Kirchhoff's rules to find the voltage across the 5.0- resistor. SOLUTION Applying the loop rule to the left loop (and suppressing units for onvenience) gives 5 .0 I 0 .0 I32 .0 1 0 .0 (1) 11 Similarly, for the right loop, 1 0 .0 I 0 .0 I .0 1 5 .0 21 32 (2) If we apply the junction rule to the upper junction, we obtain I 1I 2I 3 (3) Chapter 20 Problems 51 Subtracting Equation (2) from Equation (1) gives 5 .0 I – 1 0 .0 I 5 .0 1 2– (4) We now multiply Equation (3) by 10 and add the result to Equation (2); the result is 1 0 .0 I 0 .0 I 3 .0 12 21 (5) If we then multiply Equation (4) by 2 and add the result to Equation (5), we obtain 2 0 .0 I .0 0 .1 5 A 13 1 , or solving for I1, we obtain I . The fact that I is positive means that 1 the current in the drawing has the correct direction. The voltage across the 5.0- resistor can be found from Ohm's law: V ( 0 .1 5 A ) ( 5 .0 )=0 .7 5 V Current flows from the higher potential to the lower potential, and the current through the e f te n d o ft h e r e s i s t o r is at the higher potential. 5.0- flows from left to right, so the l ______________________________________________________________________________ 78. REASONING In preparation for applying Kirchhoff’s rules, we now choose the currents in each resistor. The directions of the currents are arbitrary, and should they be incorrect, the currents will turn out to be negative quantities. Having chosen the currents, we also mark the ends of the resistors with the plus and minus signs that indicate that the currents are directed from higher (+) toward lower () potential. These plus and minus signs will guide us when we apply Kirchhoff’s loop rule. + 2.00 Ω B + 8.00 Ω E SOLUTION Applying the junction ruleAto junction B, we find I2 I1 I I 6.00 V 1 3 I 2 + (1) + + u to fj u n c t i o n n t o j u n c t i o nO 3.00 VI 9.00 V I3 4.00 Ω we obtain Applying the loop rule to loop ABCD (going clockwise around the loop), +. I 2 . 0 0 6 . 0 0 V I 4 . 0 0 3 0 0 V 1 3 D P o t e n t i a l d r o p s P o t e n t i a l r i s e s C F (2) Applying the loop rule to loop BEFC (going clockwise around the loop), we obtain I 8 . 0 0 9 . 0 0 V I 4 . 0 0 6 . 0 0 V 0 2 3 P o t e n t i a l d r o p s P o t e n t i a l r i s e s (3) 52 ELECTRIC CIRCUITS Substituting I2 from Equation (1) into Equation (3) gives I I 8 . 0 0 9 . 0 0 V I 4 . 0 0 6 . 0 0 V 0 1 3 3 I 8 . 0 0 I 1 2 . 0 0 1 5 . 0 0 V 0 1 3 ( 4 ) Solving Equation (2) for I1 gives I 4 .5 0 A I .0 0 2 1 3 This result may be substituted into Equation (4) to show that 4 . 5 0 A2 I 0 0 8 . 0 0 I 1 2 . 0 0 1 5 . 0 0 V 0 . 3 3 5 1 . 0 0 V I 2 8 . 0 0 5 1 . 0 0 V 0o rI 1 . 8 2 A 3 3 2 8 . 0 0 h e c u r r e n t i n t h e 4 . 0 0 r e s i s t o r i s d i r e c t e d d o w n w a r d The minus sign indicates that t . + – 40 .0 .0 70 B I70 + I40 + I 60 60.0 A I20 + – C – I 50 – – + 50 .0 .0 20 79. REASONING To find the voltage between points B and D, we will find the current in the 60.0- resistor and then use Ohm’s law to find the voltage as V = IR. To find the current we will use Kirchhoff’s laws, the setup for which is shown in the circuit diagram at the right. In this diagram we have marked the current in each resistor. It is I60 that we seek. Note that we have marked each resistor with plus and minus signs, to denote which end of the resistor is at the higher and which end is at the lower potential. Given our choice for the current directions, the plus and minus signs must be those shown, and they will help us apply Kirchhoff’s loop rule correctly. If our value for I60 turns out to be negative, it will mean that the actual direction for this current is opposite to that in the diagram. D 20.0 V SOLUTION Applying the junction rule to junctions B and D gives I I I 4 0 6 0 7 0 A t j u n c t i o n B ( 1 ) I I I 6 0 2 0 5 0 ( 2 ) A t j u n c t i o n D Applying the loop rule to loops ABD, BCD, and ADC (including the battery) gives Chapter 20 Problems I 4 0 .0 I 6 0 .0 I202 0 .0 o r I4 .0 0 I6 .0 0 I20 4 0 6 0 02 03 1 4444 424 4444 3 14 424 4 3 P o te n tia ld ro p s , lo o pA B D P o te n tia lris e s , lo o pA B D I 7 0 .0 I505 0 .0 I6 6 0 .0 o r I7 .0 0 I505 .0 0 I6 .0 0 7 0 07 06 1 4 4244 3 14444 4240 444 4 3 P o te n tia ld ro p s , lo o pB C D P o te n tia lris e s , lo o pB C D I 2 0 .0 I 5 0 .0 1 2 0 .0 V r I202 .0 0 I505 .0 0 2 .0 0 2 0 5 0 4 2 4 3 o 1 4444 424 444 4 3 P o te n tia ld ro p s , lo o pA D C P o te n tia lris e s , lo o pA D C 53 (3) (4) (5) Equations (1)– (5) are five equations in five unknowns and must be solved simultaneously. Remember that it is I60 we seek, so our approach will be to eliminate the other four unknowns. Substituting I50 from Equation (2) into Equation (5) gives I .0 0 I6 .0 0 2 .0 0 2 07 05 (6) Substituting I40 from Equation (1) into Equation (3) gives I .0 0 I7 .0 0 I20 6 05 02 (7) Solving Equation (5) for I50 and substituting the result into Equation (4) gives I .0 0 2 .0 0 – I .0 0 I6 .0 0 7 07 2 02 06 (8) Solving Equation (8) for I70 and substituting the result into Equation (7) gives I 7 .0 –I201 1 .0 – 4 .0 0 6 04 (9) Solving Equation (6) for I20 and substituting the result into Equation (9) gives 2 .0 0 – I .0 0 6 05 I 7 .0 – 1 .0 – 4 .0 0 1 6 04 7 .0 0 o r I 0 .0 1 5 6 A 6 0– Since this result is negative, the current in the 60.0- resistor is opposite to that shown in the diagram in the reasoning step, that is, from point D up toward point B. Thus, point D is at a higher potential than point B, because conventional current is always directed from the high toward the low potential. Using Ohm’s law, we find that the voltage between D and B is V I 0 .0 1 5 6 A 6 0 .0 0 .9 4 V ,w i t h p o i n tD a tt h e h i g h e rp o t e n t i a l 6 0R ______________________________________________________________________________ 54 ELECTRIC CIRCUITS 80. REASONING The drawing shows a galvanometer that is being used as a voltmeter to measure the potential difference between the points A and B. The coil resistance is RC and the series resistance is R. The voltage VAB between the points A and B is equal to the voltage across the coil resistance RC plus the voltage across the series resistance R. R RC G 1 1I A B VAB SOLUTION Ohm’s law (Equation 20.2) gives the voltage across the coil resistance as I RC and that across the series resistor as I R. Thus, the voltage between A and B is V IR A BIR C Solving this equation for R yields 3 V I R 1 0 . 0 V 0 . 4 0 0 1 0 A 6 0 . 0 4 A B C R 2 . 4 9 1 0 3 I 0 . 4 0 0 1 0 A ______________________________________________________________________________ 81. R c = 50.0 SSM REASONING Since only 0.100 mA out of G the available 60.0 mA is needed to cause a full-scale 59.9 mA deflection of the galvanometer, the shunt resistor must 0.100 mA B A allow the excess current of 59.9 mA to detour around Shunt the meter coil, as the drawing at the right indicates. resistor R The value for the shunt resistance can be obtained by 60.0 mA recognizing that the 50.0- coil resistance and the shunt resistance are in parallel, both being connected between points A and B in the drawing. Thus, the voltage across each resistance is the same. SOLUTION Expressing voltage as the product of current and resistance, we find that 0A .1 0 01 0A 0 59.91 R 50.0 – 3 – 3 V o lta g e a c r o s ss h u n tr e s is ta n c e V o lta g e a c r o s sc o ilr e s is ta n c e 0A 0.1001 50.0 R 0 .0 8 3 5 – 3 – 3 5 9 .91 0A Chapter 20 Problems 55 ______________________________________________________________________________ 82. REASONING According to Ohm’s law and under full-scale conditions, the voltage V across the equivalent resistance Req of the voltmeter is V = IReq, where I is the full-scale current of the galvanometer. The full-scale current is not given in the problem statement. However, it is the same for both voltmeters. By applying Ohm’s law to each voltmeter, we will be able to eliminate the current algebraically and calculate the full-scale voltage of voltmeter B. SOLUTION Applying Ohm’s law to each voltmeter under full-scale conditions, we obtain V I R n dV I R A e q , Aa B e q , B Dividing these two equations and eliminating the full-scale current I give 5 I R R R V . 4 4 1 0 e q , B e q , B e q , B 1 B o r V V 5 0 . 0 V 3 0 . 0 V 5 B A V I R R R 2 . 4 0 1 0 A e q , A e q , A e q , A 83. REASONING As discussed in Section 20.11, some of the current (6.20 mA) goes directly through the galvanometer and the remainder I goes through the shunt resistor. Since the resistance of the coil RC and the shunt resistor R are in parallel, the voltage across each is the same. We will use this fact to determine how much current goes through the shunt resistor. This value, plus the 6.20 mA that goes through the galvanometer, is the maximum current that this ammeter can read. SOLUTION The voltage across the coil resistance is equal to the voltage across the shunt resistor, so 3 3 6 . 2 0 1 0 A 2 0 . 0 I 2 4 . 8 1 0 V o l t a g e a c r o s s c o i l r e s i s t a n c e V o l t a g e a c r o s s s h u n t r e s i s t o r So I = 5.00 A. The maximum current is 5.00 A + 6.20 mA = 5.01 A . ______________________________________________________________________________ 84. REASONING AND SOLUTION For the 20.0 V scale V1 = I(R1 + Rc) For the 30.0 V scale V2 = I(R2 + Rc) Subtracting and rearranging yields 56 ELECTRIC CIRCUITS V V 3 0 . 0 V 2 0 . 0 V – 3 2 1 I 8 . 0 0 1 0 A R R 2 9 3 0 1 6 8 0 2 1 2 0 . Substituting this value into either of the equations for V1 or V2 gives Rc = 8 ______________________________________________________________________________ 85. REASONING AND SOLUTION I R a. According to Ohm's law (Equation 20.2, V ) the current in the circuit is I V V R R 2 R The voltage across either resistor is IR, so that we find VV 6 0 . 0 V I R R 3 0 . 0 V 2 R2 2 – 3A 3 /I( 6 0 .0 V ) / ( 5 .0 0 1 0 )= 1 2 .0 1 0 b. The voltmeter’s resistance is R , and vV this resistance is in parallel with the resistance R = 1550 . The equivalent resistance of this parallel combination can be obtained as follows: 1 5 5 0 1 2 . 0 1 0 R R 1 1 1 v o rR 1 3 7 0 3 R R R p R R 1 5 5 0 1 2 . 0 1 0 p v v 3 The voltage registered by the voltmeter is IRp, where I is the current supplied by the battery to the series combination of the other 1550- resistor and Rp. According to Ohm’s law 6 0 .0 V I 0 .0 2 0 5A 1 5 5 0 + 1 3 7 0 Thus, the voltage registered by the voltmeter is I R .0 2 0 5 A 1 3 7 0 2 8 .1 V p0 ______________________________________________________________________________ 86. REASONING AND SOLUTION The equivalent capacitance of the circuit is 1 1 1 1 C 4 . 0 µ F 6 . 0 µ F 1 2 . 0 µ F The total charge provided by the battery is, then, or C = 2.0 µF Chapter 20 Problems 57 Q = CV = (2.0 10–6 F)(50.0 V) = 1.0 10–4 C This charge appears on each capacitor in a series circuit, so the voltage across the 4.0-µF capacitor is 4 Q 1 . 0 1 0 C V 2 5 V 1 6 C 4 . 0 1 0 F 1 ______________________________________________________________________________ 87. REASONING Our approach to this problem is to deal with the arrangement in parts. We will combine separately those parts that involve a series connection and those that involve a parallel connection. SOLUTION The 24, 12, and 8.0-F capacitors are in series. Using Equation 20.19, we can find the equivalent capacitance for the three capacitors: 1 111 o r C 4 . 0 F s C 2 4 F 1 2 F 8 . 0 F s This 4.0-F capacitance is in parallel with the 4.0-F capacitance already shown in the text diagram. Using Equation 20.18, we find that the equivalent capacitance for the parallel group is C 4 . 0 F + 4 . 0 F = 8 . 0 F p This 8.0-F capacitance is between the 5.0 and the 6.0-F capacitances and in series with them. Equation 20.19 can be used, then, to determine the equivalent capacitance between A and B in the text diagram: 1 111 o r C 2 . 0 F s C 5 . 0 F 8 . 0 F 6 . 0 F s ______________________________________________________________________________ 88. REASONING A capacitor with a capacitance C stores a charge q when connected between the terminals of a battery of voltage V, according to q = CV (Equation 19.8). This equation can be used to calculate the voltage if q and C are known. In this problem we know that the two capacitors together store a total charge of 5.4 × 105 C. This is also the charge stored by the equivalent capacitor, which has the equivalent capacitance CP of the parallel combination, or CP = C1 + C2 (Equation 20.18). Thus, we can determine the battery voltage by using Equation 19.8 with the given total charge and the equivalent capacitance obtained from Equation 20.18. SOLUTION With q = qTotal and C = CP = C1 + C2 Equation 19.8 becomes 58 ELECTRIC CIRCUITS 5 q 5 . 4 1 0 C T o t a l q C V C C V o r V 9 . 0 V T o t a lP 1 2 6 6 C C 2 . 0 1 0 F 4 . 0 1 0 F 1 2 89. REASONING AND SOLUTION Let C0 be the capacitance of an empty capacitor. Then the capacitances are as follows, according to the discussion following Equation 19.10: C1 = 3.00C0 and C2 = 5.00C0 The series capacitance of the two is 1 1 1 C .5 0 C .0 0 C s 2 0 4 0 or Cs = 1.54C0 Now C0 = 1.54C0 or = 1.54 ______________________________________________________________________________ 90. REASONING a. When capacitors are wired in parallel, the total charge q supplied to them is the sum of the charges supplied to the individual capacitors, or q = q1 + q2. The individual charges can be obtained from q1 = C1V and q2 = C2V, since the capacitances, C1 and C2, and the voltage V are known. b. When capacitors are wired in series, the voltage V across them is equal to the sum of the voltages across the individual capacitors, or V = V1 + V2. However, the charge q on each capacitor is the same. The individual voltages can be obtained from V1 = q/C1 and V2 = q/C2. SOLUTION a. Substituting q1 = C1V and q2 = C2V (Equation 19.8) into q = q1 + q2, we have q q q C V C V C C V 1 21 2 1 2 6 6 4 2 . 0 0 1 0 F 4 . 0 0 1 0 F 6 0 . 0 V 3 . 6 0 1 0 C b. Substituting V1 = q/C1 and V2 = q/C2 (Equation 19.8) into V = V1 + V2 gives q q VVV 12 C 1 C 2 Solving this relation for q, we have Chapter 20 Problems 59 V 6 0 . 0 V 5 q 8 . 0 0 1 0 C 1 1 1 1 6 6 C C 2 . 0 0 1 0 F 4 . 0 0 1 0 F 1 2 ______________________________________________________________________________ 91. REASONING AND SOLUTION The charges stored on capacitors in series are equal and equal to the charge separated by the battery. The total energy stored in the capacitors is 2 2 Q Q E n e r g y 2 C C 1 2 2 2 Q 1 1 E n e r g y 2 CC 1 2 According to Equation 20.19, the quantity in the parentheses is just the reciprocal of the equivalent capacitance C of the circuit, so 2 Q E nergy 2 C ______________________________________________________________________________ 92. REASONING AND SOLUTION The 7.00 and 3.00-F capacitors are in parallel. According to Equation 20.18, the equivalent capacitance of the two is 7.00 F + 3.00 F = 10.0 F. This 10.0-F capacitance is in series with the 5.00-F capacitance. According to Equation 20.19, the equivalent capacitance of the complete arrangement can be obtained as follows: 1 1 1 1 – 1 = 0 . 3 0 0 F o r C – 3 . 3 3 F 1 C 1 0 . 0 F 5 . 0 0 F 0 . 3 0 0 F The battery separates an amount of charge Q = CV = (3.33 10–6 F)(30.0 V) = 99.9 10–6 C This amount of charge resides on the 5.00 µF capacitor, so its voltage is V5 = (99.9 10–6 C)/(5.00 10–6 F) = 20.0 V The loop rule gives the voltage across the 3.00 µF capacitor to be V3 = 30.0 V – 20.0 V = 10.0 V 60 ELECTRIC CIRCUITS This is also the voltage across the 7.00 µF capacitor, since it is in parallel, so V7 = . ______________________________________________________________________________ 93. REASONING When two or more capacitors are in series, the equivalent capacitance of the 1 1 1 1 .... Equation 20.18 combination can be obtained from Equation 20.19, C s C 1 C 2 C 3 gives the equivalent capacitance for two or more capacitors in parallel: 2 C C ... The energy stored in a capacitor is given by 1C V pC 1C 2 3. , according to 2 1 2 V Equation 19.11. Thus, the energy stored in the series combination is 2C s s, where 1 1 1 1 – 1 0 . 4 7 6 F o r C – 2 . 1 0 F s 1 C 7 . 0 F 3 . 0 F 0 . 4 7 6 F s Similarly, the energy stored in the parallel combination is 1 2 C V 2 ppwhere C 7 . 0 F 3 . 0 F 1 0 . 0 F p The voltage required to charge the parallel combination of the two capacitors to the same total energy as the series combination can be found by equating the two energy expressions p. and solving for V SOLUTION Equating the two expressions for the energy, we have 1 2 1 2 C V C V 2 s s 2 pp Solving for V p , we obtain the result C 2 . 1 0 F s V V 2 4 V 1 1 V p s C 1 0 . 0 F p ______________________________________________________________________________ 94. REASONING AND SOLUTION Charge is conserved during the re-equilibrium. Therefore, using q0 and qf to denote the initial and final charges, respectively, we have q10 + q20 = 18.0 µC = q1f + q2f (1) After equilibrium has been established the capacitors will have equal voltages across them, since they are connected in parallel. Thus, Vf = q1f/C1 = q2f/C2, which leads to q1f = q2f(C1/C2) = q2f (2.00 µF)/(8.00 µF) = 0.250 q2f Chapter 20 Problems 61 Substituting this result into Equation (1) gives 18.0 µC = 0.250 q2f + q2f or q2f = 14.4 µC Hence, Vf = q2f/C2 = (14.4 10–6 C)/(8.00 10–6 F) = ______________________________________________________________________________ 95. REASONING The charge q on a discharging capacitor in a RC circuit is given by –t/RC Equation 20.22: qqe , where q0 is the original charge at time t = 0 s. Once t (time 0 for one pulse) and the ratio q / q0 are known, this expression can be solved for C. SOLUTION Since the pacemaker delivers 81 pulses per minute, the time for one pulse is 1 m i n 6 0 . 0 s 0 . 7 4 s / p u l s e 8 1 p u l s e s 1 . 0 0 m i n ) Since one pulse is delivered every time the fully-charged capacitor loses 63.2% of its original charge, the charge remaining is 36.8% of the original charge. Thus, we have q(0.368)q0, or q/q0 0.368. From Equation 20.22, we have q e–t/RC q0 Taking the natural logarithm of both sides, we have, q t ln q R C 0 Solving for C, we find t ( 0 . 7 4 s ) 7 C 6 4 . 1 1 0 F R l n ( q / q ) ( 1 . 8 1 0 ) l n ( 0 . 3 6 8 ) 0 ______________________________________________________________________________ 96. REASONING AND SOLUTION According to Equation 20.21, we find that 3 . 0 s 4 R 2 . 0 10 – 6 C 150 10 F ______________________________________________________________________________ 97. REASONING The time constant of an RC circuit is given by Equation 20.21 as = RC, where R is the resistance and C is the capacitance in the circuit. The two resistors 62 ELECTRIC CIRCUITS are wired in parallel, so we can obtain the equivalent resistance by using Equation 20.17. The two capacitors are also wired in parallel, and their equivalent capacitance is given by Equation 20.18. The time constant is the product of the equivalent resistance and equivalent capacitance. SOLUTION The equivalent resistance of the two resistors in parallel is 11 1 3 o rR 1 . 3 k P R 2 . 0 k 4 . 0 k 4 . 0 k P (20.17) The equivalent capacitance is C 3 . 0 F 6 . 0 F = 9 . 0 F P (20.18) The time constant for the charge to build up is R C 1 . 3 1 0 9 . 0 1 0 F 1 . 2 1 0 s 6 3 2 P P ______________________________________________________________________________ 98. REASONING The charging of a capacitor is described by Equation 20.20, which provides a direct solution to this problem. SOLUTION According to Equation 20.20, in a series RC circuit the charge q on the capacitor at a time t is given by qq et/ 01 where q0 is the equilibrium charge that has accumulated on the capacitor after a very long time and τ is the time constant. For q0.800q0 this equation becomes t / t / q 0 . 8 0 0 q q 1 e o r0 . 2 0 0 e 0 0 Taking the natural logarithm of both sides of this result gives t t / l n 0 . 2 0 0 l n e o rl n 0 . 2 0 0 Therefore, the number of time constants needed for the capacitor to be charged to 80.0% of its equilibrium charge is t l n 0 . 2 0 0 1 . 6 1 1 . 6 1 63 Chapter 20 Problems 99. REASONING In either part of the drawing the time constant τ of the circuit is RCeq , according to Equation 20.21, where R is the resistance and Ceq is the equivalent capacitance of the capacitor combination. We will apply this equation to both circuits. To obtain the equivalent capacitance, we will analyze the capacitor combination in parts. For the parallel CC 2 C ... applies (Equation 20.18), while for the series capacitors capacitors C P 1 3 1 1 1 1 C C C C . . .applies (Equation 20.19). S 1 2 3 C C C R R SOLUTION Using Equation 20.21, we write the time constant of each circuit as follows: C C C R C n d R C a e q , a a b e q , b + + Dividing these two equations allows us to eliminate the unknown resistance algebraically: (a) (b) R C C e q , b e q , b b o r b a C C a R e q , a q , a e (1) To obtain the equivalent capacitance in part a of the drawing, we note that the two capacitors in series in each branch of the parallel combination have an equivalent capacitance CS that can be determined using Equation 20.19 1 11 1 o rC C S 2 C C C S (2) Using Equation 20.18, we find that the parallel combination in part a of the drawing has an equivalent capacitance of 1 1 C C CC e q ,a 2 2 (3) To obtain the equivalent capacitance in part b of the drawing, we note that the two capacitors 1 in series have an equivalent capacitance of 2 C , according to Equation (2). The two capacitors in parallel have an equivalent capacitance of 2C, according to Equation 20.18. 1 Finally, then, we have a series combination of 2 C and 2C, for which Equation 20.19 applies: 1 115 2 o rC C e q , b 5 1 C C 2 C 2 C e q , b2 Using Equations (3) and (4) in Equation (1), we find that (4) C C 64 ELECTRIC CIRCUITS 2 C C e q , b 5 0 . 7 2 s 0 . 2 9 s ba C C e q , a 100. REASONING AND SOLUTION a. According to Equation 20.6c, the resistance is 2 V 1 2 V R 4 . 4 P3 3 W 2 b. According to Equation 20.6a, the current is P3 3 W I 2 . 8 A V1 2 V ______________________________________________________________________________ 101. REASONING AND SOLUTION The equivalent capacitance of the combination can be 1 1 1 1 .... obtained immediately from Equation 20.19, C s C 1 C 2 C 3 1 1 1 1 1 – 1 0 . 5 8 7 F o r C 1 . 7 F s – 1 C 3 . 0 F 7 . 0 F 9 . 0 F 0 . 5 8 7 F s ______________________________________________________________________________ 102. REASONING Electric current is the amount of charge flowing per unit time (see Equation 20.1). Thus, the amount of charge is the current times the time. Furthermore, the potential difference is the difference in electric potential energy per unit charge (see Equation 19.4), so that, once the amount of charge has been calculated, we can determine the energy by multiplying the potential difference by the charge. SOLUTION a. According to Equation 20.1, the current I is the amount of charge q divided by the time t, or I = q/t. Therefore, the additional charge that passes through the machine in normal mode versus standby mode is q I t I t I I t a d d i t i o n a l n o r m a l s t a n d b y n o r m a l s t a n d b y q i n n o r m a l m o d e q i n s t a n d b y m o d e 0 . 1 1 0 A 0 . 0 6 7 A 6 0 . 0 s 2 . 6 C Chapter 20 Problems 65 b. According to Equation 19.4, the potential difference V is the difference (EPE) in the electric potential energy divided by the charge qadditional, or V = (EPE)/qadditional. As a result, the additional energy used in the normal mode as compared to the standby mode is E P E q V 2 . 6 C 1 2 0 V 3 1 0 J a d d i t i o n a l I R 103. REASONING AND SOLUTION Ohm's law (Equation 20.2), V , gives the result directly: V 9 .0 V R 8 2 I 0 .1 1 A ______________________________________________________________________________ 104. REASONING First, we draw a current I1 (directed to the right) in the 6.00-resistor. We can express I1 in terms of the other currents in the circuit, I and 3.00 A, by applying the junction rule to the junction on the left; the sum of the currents into the junction must equal the sum of the currents out of the junction. I I . 0 0 A o rI I 3 . 0 0 A 13 1 C u r r e n t i n t o C u r r e n t o u t o f j u n c t i o n o n j u n c t i o n o n l e f t l e f t In order to obtain values for I and V we apply the loop rule to the top and bottom loops of the circuit. SOLUTION Applying the loop rule to the top loop (going clockwise around the loop), we have 3 . 0 0 A 4 . 0 0 3 . 0 0 A 8 . 0 0 2 4 . 0 V + I 3 . 0 0 A 6 . 0 0 P o t e n t i a l d r o p s P o t e n t i a l r i s e s This equation can be solved directly for the current; I 5.00A. Applying the loop rule to the bottom loop (going counterclockwise around the loop), we have I 3 . 0 0 A 6 . 0 0 2 4 . 0 V + I 2 . 0 0 V P o t e n t i a l d r o p s P o t e n t i a l r i s e s Substituting I = 5.00 A into this equation and solving for V gives V 46.0V. ______________________________________________________________________________ 66 ELECTRIC CIRCUITS 105. REASONING AND SOLUTION From Equation 20.5 we have that R = R0[1 + (T – T0)]. Solving for T gives R 9 9 . 6 1 1 R 1 2 5 0 T T 2 0 . 0 C 3 4 . 6 C 0 3 1 3 . 7 2 1 0 ( C ) ______________________________________________________________________________ 106. REASONING The magnitude q of the charge on one plate of a capacitor is given by Equation 19.8 as q = CV1, where C = 9.0 F and V1 is the voltage across the capacitor. Since the capacitor and the resistor R1 are in parallel, the voltage across the capacitor is equal to the voltage across R1. From Equation 20.2 we know that the voltage across the 4.0- resistor is given by V1 = IR1, where I is the current in the circuit. Thus, the charge can be expressed as q C V C IR 1 1 The current is equal to the battery voltage V divided by the equivalent resistance of the two resistors in series, so that V V I R R R S 1 2 Substituting this result for I into the equation for q yields V q C I R C R 1 1 RR 1 2 SOLUTION The magnitude of the charge on one of the plates is 1 2 V V 6 5 q C R 9 . 0 1 0 F 4 . 0 7 . 2 1 0 C 1 R R 4 . 0 2 . 0 1 2 ______________________________________________________________________________ 107. REASONING AND SOLUTION The voltages across the galvanometer and shunt resistances are equal since they are in parallel, so IgRg = IsRs or Ig Rs Rg I s where Ig = 0.150 10–3 A and Is = 4.00 10–3 A – 0.150 10–3 A. Then Chapter 20 Problems 67 3 0 . 1 5 0 1 0 A R 1 2 . 0 0 . 4 6 8 s 3 3 . 8 5 1 0 A The equivalent parallel resistance can be obtained as follows: 11 1 o r R 0 . 4 5 0 p R 0 . 4 6 8 1 2 . 0 p ______________________________________________________________________________ 108. REASONING The power Pn delivered to any one of the three resistors is equal to the product of the current squared (I 2) and the resistance Rn, or Pn = I 2Rn, where n = 1, 2, or 3. In each case, the resistance is known, and Ohm’s law can be used to find the current. Ohm’s law states that the current in the circuit (which is also the current through each of the resistors) equals the voltage V of the battery divided by the equivalent resistance RS of the three resistors: I = V/RS. Since the resistors are connected in series, we can obtain the equivalent resistance by adding the three resistances. SOLUTION The power Pn supplied to any one of the three resistors is 2 P I R n 1 ,2 ,o r 3 ) n n ( (20.6b) The current I depends on the voltage V of the battery and the equivalent resistance RS of the three resistors through Ohm’s law: I V RS (20.2) Substituting Equation 20.2 into Equation 20.6b gives 2 V 2 P I R Rn 1 , 2 , o r 3 ) n n n( R S (1) Since the three resistors are wired in series, the equivalent resistance RS is the sum of the R R R resistances: R S 1 2 3(Equation 20.16). Substituting this relation into Equation (1) yields 2 2 V V P R R ( n 1 , 2 , o r 3 ) n n n R R R R S 1 2 3 The power delivered to each resistor is: 68 ELECTRIC CIRCUITS 2 2 V 4 V 2 P R 2 . 0 8 . 0 W 1 1 R R R 2 . 0 4 . 0 6 . 0 1 2 3 2 2 2 2 V 4 V 2 P R 4 . 0 1 6 W 2 2 R R R 2 . 0 4 . 0 6 . 0 1 2 3 V 4 V 2 P R 6 . 0 2 4 W 3 3 R R R 2 . 0 4 . 0 6 . 0 1 2 3 ______________________________________________________________________________ 109. REASONING When two or more resistors are in series, the equivalent resistance is given RR 2 R .... When resistors are in parallel, the expression by Equation 20.16: R s 1 3 1 1 1 1 .... to be solved to find the equivalent resistance is Equation 20.17: R p R 1 R 2 R 3 We will use these relations to determine the eight different values of resistance that can be obtained by connecting together the three resistors: 1.00, 2.00, and 3.00 . SOLUTION When all the resistors are connected in series, the equivalent resistance is the .0 0 . When all three are in sum of all three resistors and the equivalent resistance is 6 .5 4 5 . parallel, we have from Equation 20.17, the equivalent resistance is 0 We can also connect two of the resistors in parallel and connect the parallel combination in series with the third resistor. When the 1.00 and 2.00- resistors are connected in parallel and the 3.00- resistor is connected in series with the parallel combination, the equivalent .6 7 . When the 1.00 and 3.00- resistors are connected in parallel and resistance is 3 the 2.00- resistor is connected in series with the parallel combination, the equivalent .7 5 . When the 2.00 and 3.00- resistors are connected in parallel and resistance is 2 .0 0 - resistor is connected in series with the parallel combination, the equivalent the 1 .2 0 . resistance is 2 We can also connect two of the resistors in series and put the third resistor in parallel with the series combination. When the 1.00 and 2.00- resistors are connected in series and the 3.00- resistor is connected in parallel with the series combination, the equivalent .5 0 . When the 1.00 and 3.00- resistors are connected in series and the resistance is 1 2.00- resistor is connected in parallel with the series combination, the equivalent .3 3 . Finally, when the 2.00 and 3.00- resistors are connected in series resistance is 1 and the 1.00- resistor is connected in parallel with the series combination, the equivalent .8 3 3 . resistance is 0 Chapter 20 Problems 69 ______________________________________________________________________________ 110. REASONING AND SOLUTION The resistance of the parallel combination is given by 1 1 1 R .0 0 p R 2 and the series combination has a resistance of Rs = R + 2.00 . Ohm's law gives for each case VV V I p R .0 0 p R2 and V V I s R 2 .0 0 s R We know that Ip = 5Is. Using this with the above equations and suppressing units yields the quadratic equation R2 – 6.0R + 4.00 = 0 The two solutions for R in this equation are 5.24 and 0.76 . ______________________________________________________________________________ 111. REASONING a. The greatest voltage for the battery is the voltage that generates the maximum current I that the circuit can tolerate. Once this maximum current is known, the voltage can be calculated according to Ohm’s law, as the current times the equivalent circuit resistance for the three resistors in series. To determine the maximum current we note that the power P dissipated in each resistance R is P I 2R according to Equation 20.6b. Since the power rating and resistance are known for each resistor, the maximum current that can be tolerated by a resistor is I P/ R . By examining this maximum current for each resistor, we will be able to identify the maximum current that the circuit can tolerate. b. The battery delivers power to the circuit that is given by the battery voltage times the current, according to Equation 20.6a. SOLUTION a. Solving Equation 20.6b for the current, we find that the maximum current for each resistor is as follows: P 4 . 0 W 1 0 . 0 W 5 . 0 W I 1 . 4 A I 0 . 9 1 3 A I 1 . 3 A R 2 . 0 1 2 . 0 3 . 0 2 . 0 r e s i s t o r 1 2 . 0 r e s i s t o r 3 . 0 r e s i s t o r 70 ELECTRIC CIRCUITS The smallest of these three values is 0.913 A and is the maximum current that the circuit can tolerate. Since the resistors are connected in series, the equivalent resistance of the circuit is R 2 . 0 1 2 . 0 3 . 0 1 7 . 0 S Using Ohm’s law with this equivalent resistance and the maximum current of 0.913 A reveals that the maximum battery voltage is V I R 0 . 9 1 3 A 1 7 . 0 1 5 . 5 V S b. The power delivered by the battery in part (a) is given by Equation 20.6a as P I V 0 . 9 1 3 A 1 5 . 5 V 1 4 . 2 W 112. REASONING AND SOLUTION a. In the first case the parallel resistance of the 75.0 and the 45.0 resistors have an equivalent resistance that can be calculated using Equation 20.17: 1 1 1 R 5 .0 4 5 .0 p 7 o r R 8 .1 p2 Ohm’s law, Emf = IR gives Emf = (0.294 A)(28.1 + r), or Emf = 8.26 V + (0.294 A)r (1) In the second case, Emf = (0.116 A)(75.0 + r), or Emf = 8.70 V + (0.116 A)r (2) Multiplying Equation (1) by 0.116 A, Equation (2) by 0.294 A, and subtracting yields Emf = b. Substituting this result into Equation (1) and solving for r gives r = 2.5 . ______________________________________________________________________________ 113. REASONING The resistance of a metal wire of length L, cross-sectional area A and resistivity is given by Equation 20.3: R L/ A. The volume V2 of the new wire will be the same as the original volume V1 of the wire, where volume is the product of length and cross-sectional area. Thus, V1 = V2 or A1L1 = A2L2. Since the new wire is three times longer than the first wire, we can write Chapter 20 Problems 71 A L L ( 3 L ) o r A /3 1 1A 2 2A 2 1 2A 1 2, and find the We can form the ratio of the resistances, use this expression for the area A new resistance. SOLUTION The resistance of the new wire is determined as follows: 3 L A RL / A L A 2 22 2 1 1 1 9 R / A A A / 3 1 L 1 1L 1 2L 1 1 2, we find that Solving for R R R (2 1 .0 ) 1 8 9 29 19 ______________________________________________________________________________ 114. REASONING The answer is not 340 W + 240 W = 580 W. The reason is that each heater contributes resistance to the circuit when they are connected in series across the battery. For a series connection, the resistances add together to give the equivalent total resistance, according to Equation 20.16. Thus, the total resistance is greater than the resistance of either heater. The greater resistance means that the current from the battery is less than when either heater is present by itself. Since the power for each heater is P = I2R, according to Equation 20.6b, the smaller current means that the power delivered to an individual heater is less when both are connected than when that heater is connected alone. We approach this problem by remembering that the total power delivered to the series combination of the heaters is the power delivered to the equivalent series resistance. SOLUTION Let the resistances of the two heaters be R1 and R2. Correspondingly, the powers delivered to the heaters when each is connected alone to the battery are P1 and P2. For the series connection, the equivalent total resistance is R1 + R2, according to Equation 20.16. Using Equation 20.6c, we can write the total power delivered to this equivalent resistance as 2 V P (1) R 1R 2 But according to Equation 20.6c, as applied to the situations when each heater is connected by itself to the battery, we have 2 V R 1 o r R 1 2 V P 2 R 2 o r 2 V R 2 P 2 P 1 2 V P 1 (2) (3) 72 ELECTRIC CIRCUITS Substituting Equations (2) and (3) into Equation (1) gives P 2 P P 4 0W 4 0W V 1 3 2 1 2 1 4 0W 2 2 1 1 P P 3 4 0 W + 2 4 0 W V V 1 2 P P P P 1 2 1 2 ______________________________________________________________________________ 115. REASONING The foil effectively converts the capacitor into two capacitors in series. Equation 19.10 gives the expression for the capacitance of a capacitor of plate area A and plate separation d (no dielectric): C0 0A/d. We can use this expression to determine the capacitance of the individual capacitors created by the presence of the foil. Then using the fact that the "two capacitors" are in series, we can use Equation 20.19 to find the equivalent capacitance of the system. SOLUTION Since the foil is placed one-third of the way from one plate of the original capacitor to the other, we have d1 (2/3)d, and d2 (1/3)d. Then 0A 3 A C 0 1 ( 2 /3 ) d 2 d and 0A 3 A C 0 2 ( 1 /3 ) d d Since these two capacitors are effectively in series, it follows that 1 1 1 1 13 d d = = C C C 3 A / 2 d 3 A / d 3 A A s 1 2 0 0 0 0 1/C0, and we have But C0 0A/d, so that d/0A 11 o r C C s 0 C sC 0 ______________________________________________________________________________ 116. REASONING AND SOLUTION The mass m of the aluminum wire is equal to the density d of aluminum times the volume of the wire. The wire is cylindrical, so its volume is equal to the cross-sectional area A times the length L; m = dAL. The cross-sectional area of the wire is related to its resistance R and length L by Equation 20.3; R = L/A, where is the resistivity of aluminum. Therefore, the mass of the aluminum wire can be written as Chapter 20 Problems 73 L L m d A L d R The resistance R is given by Ohm’s law as R = V/I, so the mass of the wire becomes 2 L L I d m d L V R 3 8 2 ( 2 7 0 0 k g / m ) ( 2 . 8 2 1 0 m ) ( 1 7 5 m ) ( 1 2 5 A ) 2 m 9 . 7 1 0 k g 0 . 3 0 0 V ______________________________________________________________________________ 117. CONCEPT QUESTIONS a. The resistance R of a piece of material is related to its length L and cross-sectional area A by Equation 20.3, R L/ A, where is the resistivity of the material. In order to rank the resistances, we need to evaluate L and A for each configuration in terms of L0, the unit of length. Resistance Rank a 2 4 L R 0 L 2 L L 0 0 0 1 b 1 0 R L 2 L 4 L 8 L 0 0 0 3 c 1 L 0 R 2 L 4 L 2 L 0 0 0 2 Therefore, the a has the largest resistance, followed by c, and then by b. b. Equation 20.2 states that the current I is equal to the voltage V divided by the resistance, I V / R. Since the current is inversely proportional to the resistance, the largest current arises when the resistance is smallest, and vice versa. Thus, b has the largest current, followed by c, and then by a. 74 ELECTRIC CIRCUITS SOLUTION a. The resistances can be found by using the results of the Concept Questions: a b c 2 2 2 R 1 . 5 0 1 0 m 0 . 6 0 0 2 L 5 . 0 0 1 0 m 0 1 2 1 R 1 . 5 0 1 0 m 0 . 0 3 7 5 2 8 L 8 5 . 0 0 1 0 m 0 1 2 1 R 1 . 5 0 1 0 m 0 . 1 5 0 2 2 L 2 5 . 0 0 1 0 m 0 b. The current in each case is given by Equation 20.2, where the value of the resistance is obtained from part (a): . 0 0 V V3 I 5 . 0 0 A a R0 . 6 0 0 . 0 0 V V3 I 8 0 . 0 A b R0 . 0 3 7 5 . 0 0 V V3 I 2 0 . 0 A c R0 . 1 5 0 We see that the largest current is in b, with progressively smaller currents in c and a. ______________________________________________________________________________ 118. CONCEPT QUESTIONS a. The power delivered to a resistor is given by Equation 20.6c as PV / R, where V is 2 the voltage and R is the resistance. Because of the dependence of the power on V 2, doubling the voltage has a greater effect in increasing the power than halving the resistance. The table shows the power for each circuit, given in terms of these variables: Power a b c d 2 V R 2 V P 2R 2 2 V 2 4 V P R R 2 2 V 2 2 V P 2 R R P Rank 3 4 1 2 Chapter 20 Problems 75 b. The current is given by Equation 20.2 as I = V/R. Note that the current, unlike the power, depends linearly on the voltage. Therefore, either doubling the voltage or halving the resistance has the same effect on the current. The table shows the current for the four circuits: Current Rank V R V I 2R 2V I R 2V V I 2R R 2 I a b c d 3 1 2 SOLUTION a. Using the results from part (a) and the values of V = 12.0 V and R = 6.00 , the power dissipated in each resistor is Power Rank a 1 2 . 0 V V P 2 4 . 0 W R6 . 0 0 3 b 1 2 . 0 V V P 1 2 . 0 W 2 R 2 6 . 0 0 4 c 1 2 . 0 V 4 V4 P 9 6 . 0 W R 6 . 0 0 1 d 1 2 . 0 V 2 V2 P 4 8 . 0 W R 6 . 0 0 2 2 2 2 2 2 2 2 2 76 ELECTRIC CIRCUITS b. Using the results from part (b) and the values of V = 12.0 V and R = 6.00 , the current in each circuit is Current a b c Rank 2 . 0 V V1 I 2 . 0 0 A R6 . 0 0 2 . 0 V V 1 I 1 . 0 0 A 2 R 2 6 . 0 0 1 2 . 0 V 2 V2 I 4 . 0 0 A R6 . 0 0 2 3 1 1 2 . 0 V 2 V2 I 2 . 0 0 A 2 2 R 2 6 . 0 0 ______________________________________________________________________________ d 119. CONCEPT QUESTIONS a. The three resistors are in series, so the same current goes through each resistor: I1 I2 I3. The voltage across each resistor is given by Equation 20.2 as V = IR. Because the current through each resistor is the same, the voltage across each is proportional to the resistance. Since R1 R2 R3, the ranking of the voltages is V1 V2 V3. b. The three resistors are in parallel, so the same voltage exists across each: V1 V2 V3. The current through each resistor is given by Equation 20.2 as I = V/R. Because the voltage across each resistor is the same, the current through each is inversely proportional to the resistance. Since R1 R2 R3, the ranking of the currents is I3 I2 I1. SOLUTION a. The current through the three resistors is given by I = V/Rs, where Rs is the equivalent resistance of the series circuit. From Equation 20.16, the equivalent resistance is Rs = 50.0 + 25.0 + 10.0 85.0 The current through each resistor is 2 4 . 0 V V I I I 0 . 2 8 2 A 1 2 3 R 8 5 . 0 s The voltage across each resistor is V IR 0 .2 8 2A5 .0 4 .1 V 0 1 1 1 V IR 0 .2 8 2A2 .0 .0 5 V 5 7 2 2 V IR 0 .2 8 2A 0 .0 .8 2V 1 2 3 3 Chapter 20 Problems 77 b. The resistors are in parallel, so the voltage across each is the same as the voltage of the battery: V V V 2 4 .0 V 1 2 3 The current through each resistor is equal to the voltage across each divided by the resistance: V 24.0 V I1 0.480 A R1 50.0 I2 V 24.0 V 0.960 A R2 25.0 V 24.0 V 2.40 A R3 10.0 ______________________________________________________________________________ I3 120. CONCEPT QUESTION Between points a and b there is only one resistor, so the equivalent resistance is Rab = R. Between points b and c the two resistors are in parallel. The equivalent resistance can be found from Equation 20.17: 1112 1 s o R R b c 2 R R R R b c The equivalent resistance between a and b is in series with the equivalent resistance between b and c, so the equivalent resistance between a and c is 3 1 RRRRRR 2 2 a c a b b c Thus, we see that Rac > Rab > Rbc. SOLUTION Since the resistance is R = 10.0 , the equivalent resistances are: Rab R 10.0 Rbc 12 R 5.00 Rac 32 R 15.0 ______________________________________________________________________________ 121. CONCEPT QUESTION In part a, the current goes from left-to-right through the resistor. Since the current always goes from a higher to a lower potential, the left end of the resistor is + and the right end is –. In part b, the current goes from right-to-left through the resistor. 78 ELECTRIC CIRCUITS The right end of the resistor is + and the left end is –. The potential drops and rises for the two cases are: Potential drops Potential rises Part a IR V Part b V IR SOLUTION Since the current I goes from left-to-right through the 3.0- and 4.0- resistors, the left end of each resistor is + and the right end is –. The current goes through the 5.0- resistor from right-to-left, so the right end is + and the left end is –. Starting at the upper left corner of the circuit, and proceeding clockwise around it, Kirchhoff’s loop rule is written as 3 . 0 I 1 2 V + 4 . 0 I 5 . 0 I 3 6 V P o t e n t i a l r i s e s P o t e n t i a l d r o p s Solving this equation for the current gives I = 2.0 A ______________________________________________________________________________ 122. CONCEPT QUESTION When capacitors are connected in parallel, each receives the entire voltage V of the battery. Thus, the total energy stored in the two capacitors is 2 2 1 C V 1 CV 2 1 2 2 . When the capacitors are connected in series, the sum of the voltages across each capacitor equals the battery voltage: V1 V2 V. Thus, the voltage across each 2 2 1 V 1 CV capacitor is series is less than the battery voltage, so the total energy, 2C 2 2 2 , is 11 less than when the capacitors are wired in parallel. SOLUTION a. The voltage across each capacitor is the battery voltage, or 60.0 V. The energy stored in both capacitors is 1 1 1 T o t a l e n e r g y C V C V C C V 2 1 2 2 2 12 2 2 2 1 2 . 0 0 1 0 F + 4 . 0 0 1 0 F 6 0 . 0 V 1 . 0 8 1 0 J 2 6 6 2 2 b. According to the discussion in Section 20.12, the total energy stored by capacitors in 2 1 o t a le n e r g y =C V series is T 2 S , where CS is the equivalent capacitance of the series combination: 1 1 1 1 1 6 6 C C C . 0 0 1 0 F 4 . 0 0 1 0 F S 1 22 (20.19) Chapter 20 Problems 6 Solving this equation yields CS = 1.33 10 79 F. The total energy is 6 3 1 T o t a l e n e r g y 1 . 3 3 1 0 F 6 0 . 0 V 2 . 3 9 1 0 J 2 2 ______________________________________________________________________________ 123. CONCEPT QUESTIONS a. The total power P delivered by the battery is related to the equivalent resistance Req connected between the battery terminals and to the battery voltage V according to 2 Equation 20.6c: PV / Req. b. When two resistors are connected in series, the equivalent resistance RS of the combination is greater than the resistance of either resistor alone. This can be seen directly from RS R 1R 2 (Equation 20.16). c. When two resistors are connected in parallel, the equivalent resistance RP of the combination is smaller than the resistance of either resistor alone. This can be seen directly 1 1 1 by substituting values in R P R 1 R 2 (Equation 20.17) or by reviewing the discussion in Section 20.7 concerning the water flow analogy for electric current in a circuit. d. Since the total power delivered by the 2 battery is PV / Req and since the power and the battery voltage are the same in both cases, it follows that the equivalent resistances are also the same. But the parallel combination has an equivalent resistance RP that is smaller than RB, whereas the series combination has an equivalent resistance RS that is greater than RA. This means that RB must be greater than RA, as Diagram 1 at the right shows. If RA were greater than RB, as in Diagram 2, the equivalent resistances RS and RP would not be equal. Resistance Resistance RS Diagram 1 RB RA RS = RP RB RA RP Diagram 2 SOLUTION As discussed in our answer to Concept Question (d), the equivalent resistances in circuits A and B are equal. According to Equations 20.16 and 20.17, the series and parallel equivalent resistances are 80 ELECTRIC CIRCUITS R R R 2 R S A A A 1 1 1 1 o r R P2R B R R R P B B Setting the equivalent resistances equal gives 1 2 R Ro r A 2B R B 4 R A As expected, RB is greater than RA. 124. CONCEPT QUESTIONS a. The total power P delivered by the battery is related to the equivalent resistance Req connected between the battery terminals and to the battery voltage V according to 2 Equation 20.6c: PV / Req. b. We begin by recognizing that the combination of resistors in circuit A is also present in circuits B and C (see the shaded part of these circuits). In circuit B an additional resistor is in parallel with the combination from A. The equivalent resistance of resistances in parallel is always less than any of the individual resistances alone. Therefore, the equivalent resistance of circuit B is less than that of A. In circuit C an additional resistor is in series with the combination from A. The equivalent resistance of resistances in series is always greater than any of the individual resistances alone. Therefore, the equivalent resistance of circuit C is greater than that of A. We conclude then that the equivalent resistances are ranked C, A, B, with C the greatest and B the smallest. R 2 c. The total power delivered by the batteryRis PV / RR toR eq and is inversely proportional R the equivalent resistance. Since the battery voltage is the same in all three cases, this means R that the power ranking is the reverse of theR ranking deduced in Concept Question (b). InR R other words, from greatest to smallest, the total power delivered by the battery is B, A, C. 2 + is + battery SOLUTION The total power delivered by the is PV / Req. The voltage given, but we must determine the equivalent resistance in each case. In circuit VA each V branch of the parallel combination consists ofAtwo resistances R in series. Thus, B the R R R 2 R resistance of each branch is eq , according to Equation 20.16. The two R R from Equation parallel branches have an equivalent resistance that can be determined 20.17 R as R R + V Chapter 20 Problems 81 1 11 o r RR A R 2 RR 2 A In circuit B the resistance of circuit A is in parallel with an additional resistance R. According to Equation 20.17, the equivalent resistance of this combination is 111 1 1 1 = +o rRR B 2 R R R R R BA In circuit C the resistance of circuit A is in series with an additional resistance R. According to Equation 20.16, the equivalent resistance of this combination is R R R R R 2 R C A 2 We can now use PV / Req to determine the total power delivered by the battery in each case: CircuitA V2 6.0V P 4.0W R 9.0 CircuitB V2 6.0V P1 1 8.0W R 29.0 2 CircuitC V2 6.0V P 2.0W 2R 29 .0 2 2 2 These results are consistent with our answer to Concept Question (c). ______________________________________________________________________________