Download Ay 102: Homework 5 (Blast waves, Supernova Remnant) S. R. Kulkarni

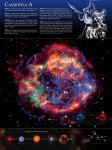
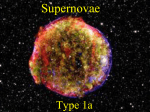
Ay 102: Homework 5 (Blast waves, Supernova Remnant)
S. R. Kulkarni
March 7, 2016
Please come to the class reading either Ch 38-39 of Draine or 16.1-16.3 of Kowk. I would
like that each of be prepared to work out successive elements of this “homework” on the
board (with constructive help from me).
1. Supernova Remnant. A popular model for a type Ia supernova is one where a C+O
white dwarf accretes matter from a companion and upon reaching the Chandrashekar
mass explodes. Let the progenitor be located say 200 pc in the WNM (n0 = 1 cm−3 and
T = 4, 000 K).
1. Assuming that half of the mass of the white dwarf burns (from C+O) to Iron estimate
the yield of explosive energy, E0 .
2. The explosive energy heats the debris and there is rapid expansion. What is the
mean velocity of expansion of the debris?
3. The debris starts interacting with the surrounding ISM. The first phase, free expansion, ends when the debris has swept up matter comparable to its own mass.
Estimate the age of the supernova remnant (SNR).
4. What is the temperature and density of the post-shock gas? What is the isobaric
cooling timescale for a parcel of post-shocked gas? (Cooling curve in Drain Ch 34,
given on class homepage)
5. Using the cooling curves presented in the class estimate the cooling timescale when
the post-shock gas reaches say 200 km/s. Compare this to the age of the SNR
6. In the last phase, the SNR enters a momentum conserving phase. In this phase,
the postshock temperature is low enough that cooling is very efficient and the postshock energy is rapidly radiated and the density rises. The hot interior expands
adiabatically. The interior pressure, P , drives the cool shell:
d
(Ms vs ) = P 4πRs2
dt
1
(1)
where Ms is the swept up matter and vs and Rs is the velocity and radius of the thin
shell. Assuming that the solution to this differential equation is a power law, R ∝ tη
estimate η.
7. Explain what you expect in the last phase of the SNR.
2. SNR in halo Consider the case of a two neutron stars merging in the hot halo of
the galaxy, n0 = 0.003 cm−3 and T = 106 K. The energy of explosion could be as high as
1050 erg and mass of ejecta (predominantly heavy elements) could be as much as 0.1 M .
Redo the calculations for phase 1 and phase 2.
3. Stellar Winds Consider a star with a strong stellar wind: Ṁ = 10−6 M yr−1 and
terminal velocity, vw = 103 km s−1 embedded in a medium with density, n0 . As before, free
expansion ends when the mass of the swept matter is comparable to the integrated mass of
the stellar wind. For the next phase, as before, we will assume that there is little radiative
loss. We will then further make an ansatz (verified by detailed numerical simulations) that
at any given instant the postshocked gas has equal energy in heat and motion (averaged
over all parcels of gas).
For n0 = 1 cm−3 compute the velocity of the shock as a function of time. Estimate when
the cooling timescale becomes comparable to the age of the expanding shell. Describe
qualitatively the subsequent behavior.
2