Download Happy Halloween Chapter 33 LC Circuits

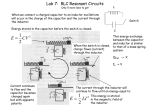
Happy Halloween
Chapter 33
LC Circuits
RC circuits (chapter 28)
A resistor and capacitor in series
!
!
Charging up a capacitor (switch to “a”)
The loop rule gives
ε
q
− iR −
=0
C
ε
dq
q
=
R+
dt
C
The solution of this differential
equation is:
−t τc
q = C ε (1 − e
)
where
τ C = RC
RC circuits (chapter 28)
!
Graphical results
q = C ε (1 − e
!
−t τc
)
ε −t τ c
dq
i=
=
e
dt
R
Initially the current flows easily, but then drops
exponentially as the capacitor get filled up.
RC circuits (chapter 28)
!
Discharging capacitor (switch to “b”)
gives the differential equation:
q
iR +
=0
C
q
dq
=0
R+
C
dt
• The solution is
q = q0 e
−t τc
τ C = RC
Emf for an Inductor (chapter 31)
N Φ B = Li
!
Self-inductance – changing current
through an inductor gives an emf
(voltage change) across the
inductor denoted by
ε
L
d ( NΦ B )
d ( Li )
=−
=−
dt
dt
ε
!
L
di
= −L
dt
Note the sign of this emf goes against
the current change
RL circuits (chapter 31 – Fig.17)
A resistor and inductor in series
!
Charging up a inductor (switch to “a”)
The loop rule gives
ε
!
di
− iR − L
=0
dt
The solution of this differential
equation is:
i=
ε
R
(1 − e
−t τ L
)
Where
L
τL =
R
is the inductive time
constant
RL circuits (chapter 31 Fig. 19)
!
Graphical results
V R = iR = ε (1 − e
!
−t τ L
)
di
VL = − L
= ε e −t τ L
dt
Initially inductor acts to oppose changes in current (i=0 ).
! Long time later, inductor acts like simple wire with (i =ε/R ).
RL circuits (chapter 31)
!
Circuit is opened (switch to “b”)
di
− iR − L
=0
dt
i=
ε
R
e
−t τ L
= i0 e
L
τL =
R
−t τ L
Energy stored in fields
!
!
Energy stored in the
electric field of a
capacitor (chapter 28)
Energy stored in the B
field of an inductor
(chapter 31)
2
U
U
E
1 q
=
2 C
B
1
Li
=
2
2
LC Circuits
!
LC Circuit – inductor &
capacitor in series
Find q, i and V vary
sinusoidally with period T
2π
(angular frequency ω)
ω=
T
!
E field of capacitor and B
!
!
field of inductor oscillate
The energy oscillates
between E field stored in
the capacitor and the B
field stored in the inductor
2
1q
UE =
2C
U
B
1
Li
=
2
2
LC Circuits
!
Total energy of LC circuit
2
2
Li
q
+
U = UB +UE =
2
2C
!
Analogy to block-spring
system (183)
U = mv + kx
1
2
2
1
2
2
LC Circuits (checkpoint #1)
!
A charged capacitor &
inductor are connected in
series at time t=0. In
terms of period, T, how
much later will the following
reach their maximums:
!
!
!
!
q of capacitor
T/2
T/2
VC with original polarity
T
Energy stored in E field
T/2
The current
T/4
LC Circuits
!
Total energy of LC circuit
Li 2 q 2
+
U = UB +UE =
2
2C
!
Total energy is constant
dU
=0
dt
!
Differentiating gives
dU d  Li
q 
di q dq
 = Li +
= 
+
=0
dt
dt  2
2C 
dt C dt
2
2
LC Circuits
2
dq
i=
dt
!
Using
!
We obtain
di d q
= 2
dt dt
2
d q 1
L 2 + q=0
dt
C
!
Solution is
!
where q is the variable, Q is the
amplitude (maximum value for q)
Q is the amplitude
ω is the angular frequency
φ is the phase
constant
q = Q cos(ωt + φ )
LC Circuits
!
The phase constant, φ, is determined by the
conditions at time t=0 (or some other time)
q = Q cos(ωt + φ )
!
If φ = 0 then at t = 0, q = Q
• I will take φ = 0 for the rest of
the lecture notes. To get the full
result when you see ωt
replace it by
ω t +φ
LC Circuits
!
Charge of LC circuit
!
Find current by
q = Q cos( ωt )
dq
i=
dt
d
i = [Q cos( ωt ) ] = −Qω sin( ωt )
dt
!
Amplitude I is
I = ωQ
i = − I sin( ωt )
LC Circuits
!
What is ω for an LC circuit?
d 2q
2
=
−
ω
Q cos( ωt )
2
dt
q = Qcos( ωt )
!
Substitute into
!
Find ω for LC circuit is
2
d q 1
L 2 + q=0
dt
C
1
2
− Lω Q cos( ωt ) + Q cos( ωt ) = 0
C
ω=
1
LC
LC Circuits
!
!
The energy stored in an LC
circuit at any time, t
q = Q cos( ωt )
Substitute
U
U
!
B
U = UB + UE
E
i = − I sin( ωt )
q2
Q2
=
=
cos
2C
2C
2
(ω t )
Li 2
L 2 2
ω Q sin
=
=
2
2
Using
ω=
1
LC
U
B
2
(ω t )
Q2
=
sin
2C
2
(ω t )
LC Circuits
!
Thus
U
U
!
!
!
E
B
Q2
=
cos
2C
Q2
=
sin
2C
2
(ω t )
2
(ω t )
2
Maximum value for both U
=
U
=
Q
2C
E ,max
B ,max
At any instant, sum is U = U B + U E = Q2 2C
When UE = max, UB = 0, and conversely,
when UB = max, UE = 0
LC Circuits (checkpoint #2)-quiz
!
Capacitor in LC circuit has VC,max = 15 V and
UE,max = 150 J. When capacitor has VC = 5 V
and UE = 50 J , what are the
!
!
!
1) emf across the inductor?
2) the energy stored in the B field?
Apply the loop rule
!
Net potential difference around the
circuit must be zero
a, b,
VL (t ) = VC (t )
UE,max = UE (t) +UB (t)
c,
d,
e
1) 0, 5, 10, 15, 20 V
2) 0, 50, 100, 150, 200 J