Download November 3rd Chapter 33 RLC Circuits

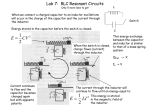
November
3rd
Chapter 33
RLC Circuits
LC Circuits
!
LC Circuit – inductor &
capacitor in series
!
Find q, i and V vary
sinusoidally with period T
(angular frequency ω)
!
The energy oscillates
between E field stored in
the capacitor and the B
field stored in the inductor
2π
ω=
= 2πf
T
2
1q
UE =
2C
U
B
1
Li
=
2
2
LC Circuits
!
Total energy of LC circuit
Li 2 q 2
+
U = UB +UE =
2
2C
!
Analogy to block-spring
system (PHY183)
U = mv + kx
1
2
2
k
ω=
m
1
2
2
LC Circuits (checkpoint #1)
!
A charged capacitor &
inductor are connected in
series at time t=0. In
terms of period, T, how
much later will the following
IL
reach their maximums:
!
!
!
!
q of capacitor
T/2
T/2
VC with original polarity
T
Energy stored in E field
T/2
The current
T/4
LC Circuits
!
The phase constant, φ, is determined by the
conditions at time t=0 (or some other time)
q = Q cos(ωt + φ )
!
If φ = 0 then at t = 0, q = Q
!
Current is
!
Where
i = − I sin( ωt )
I = ωQ
and
ω=
1
LC
LC Circuits
2
U
E
Q
=
cos
2C
2
(ω t )
2
(ω t )
2
U
!
!
!
B
Q
=
sin
2C
2
Maximum value for both U
=
U
=
Q
2C
E ,max
B ,max
At any instant, sum is U = U B + U E = Q2 2C
When UE = max, UB = 0, and conversely,
when UB = max, UE = 0
LC Circuits (checkpoint #2)-quiz
!
Capacitor in LC circuit has VC,max = 15 V and
UE,max = 150 J. When capacitor has VC = 5 V
and UE = 50 J , what are the
!
!
!
1) emf across the inductor?
2) the energy stored in the B field?
Apply the loop rule
!
Net potential difference around the
circuit must be zero
vL (t ) = vC (t )
1) 5 V - answer B
2) 100 J - answer C
UE,max = UE (t) +UB (t)
Damped oscillator
!
!
!
!
RLC circuit – resistor, inductor
and capacitor in series
Total electromagnetic energy,
U = UE + UB , is no longer
constant
Energy decreases with time as it
is transferred to thermal energy
in the resistor
Oscillations in q, i and V are
damped
!
Same as damped block and spring
RLC Circuits
!
!
!
Resistor does not store
electromagnetic energy so
total energy at any time is
2
2
Li
q
+
U = UB +UE =
2
2C
Rate of transfer to thermal
dU
2
=
−
i
R
energy is (minus sign means
dt
U is decreasing)
Differentiating gives
di q dq
dU
2
= Li +
= −i R
dt
dt C dt
RLC Circuits
di q dq
dU
2
= Li +
= −i R
dt C dt
dt
2
!
dq
Use relations i =
dt
!
Differential equation for damped RLC circuit is
di d q
= 2
dt dt
2
d q
dq
1
L
+ R
+
q = 0
2
dt
dt
C
!
Solution
q = Qe
− Rt / 2 L
cos( ω ′t )
RLC Circuits
q = Qe
− Rt / 2 L
cos( ω ′t )
ω′ = ω − ( R / 2L)
2
2
ω =
1
LC
!
Where
!
Charge in RLC circuit is sinusoidal but with an
exponentially decaying amplitude
− Rt / 2 L
Qe
!
!
Damped angular frequency, ω´, is always less
than ω of the undamped oscillations
If R is small enough can replace ω´ with ω
RLC Circuits
q = Qe
!
− Rt / 2 L
cos( ω ′t )
Find UE as function of time
2
2
q
Q − Rt / L 2
UE =
=
e
cos ( ω ′t )
2C 2C
2
!
Total energy decreases as
U tot
Q − Rt / L
=
e
2C
AC generator
!
!
!
Mechanically turn loop in B
field, induces a current and
therefore an emf
Driving angular frequency ωd is
equal to angular speed that
loop rotates in B field.
Used Faraday’s law to find emf
ε
dΦ B
= −N
= NBAω d sin ω d t
dt
ε =ε
m
sin ω d t
ε
m
= NBA ω d
ε
t
Forced Oscillations
Driving frequency ωd will overpower the natural frequency ω
Resistive load
vR = VR sin ω d t VR = ε m
Capacitive load
vC = VC sinω d t VC = ε m
Inductive load
vL = VLsinω d t VL = ε m
Forced oscillations - Resistive load
!
Use definition of resistance to
find iR
v R = V R sin ω d t
vR VR
=
sin ω d t
iR =
R
R
!
!
Voltage and current are
functions of sin(ωdt) with φ = 0
so are in phase
No damping of vR and iR , since
the generator supplies energy
Forced oscillations - Resistive load
!
Compare current to general form
vR VR
iR =
= sin ω d t
R
R
VR = I R R
iR = I Rsin(ωd t − φ )
!
!
!
Minus sign for phase is tradition
For purely resistive load the phase
constant φ = 0
Voltage amplitude is related to
current amplitude
VR
IR =
R
VR = I R R
Forced oscillations - Capacitive load
!
Use definition of capacitance
qC = Cv C = CV C sin ω d t
!
Use definition of current and
differentiate
dq C
iC =
= ω d CV C cos ω d t
dt
!
Replace cosine term with a
phase-shifted sine term
cosωd t = sin(ωd t + 90°)
Capacitive load
!
Voltage and current relations
vC = VC sin ω d t
iC = ωd CVC sin(ωd t + 90°) = IC sin(ωd t + 90°)
VC
IC =
XC
!
1
XC =
ωd C
XC is called the capacitive reactance
has units of ohms
Forced oscillations - Capacitive load
!
Compare vC and iC of capacitor
vC = VC sin ω d t
iC = ωd CVC sin(ωd t + 90°)
!
Voltage and current are out of
phase by 90°
!
Current leads voltage by T/4
Forced Oscillations - Inductive load
!
Voltage and current relations
v L = V L sin ω d t
VL
iL =
sin(ωd t − 90°) = I L sin(ωd t − 90°)
ωd L
VL
IL =
XL
!
X L = ωd L
XC is called the inductive reactance has
units of ohms
Forced Oscillations - Inductive load
!
Compare vL and iL of
inductor
vL = VL sin ω d t
iL = I L sin (ω d t − 90°)
!
!
!
Compare iL to vL
iL and vL are 90° out of
phase
Current lags voltage by T/4
Summary of Forced Oscillations
Element
Resistor
Reactance/
Resistance
R
Phase of Phase Amplitude
Current angle φ Relation
In phase
0°
VR=IRR
Capacitor XC= 1/ωdC Leads vC -90°
(ICE)
Inductor
+90°
XL=ωdL Lags vL
(ELI)
!
VC=ICXC
VL=ILXL
ELI (positively) is the ICE man
!
!
!
Voltage or emf (E) before current (I) in an inductor (L)
Phase constant φ is positive for an inductor
Current (I) before voltage or emf (E) in capacitor (C)