* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Outline Applications of Random Networks Complex Networks, Course 303A, Spring, 2009
Distributed firewall wikipedia , lookup
Recursive InterNetwork Architecture (RINA) wikipedia , lookup
Computer network wikipedia , lookup
Zero-configuration networking wikipedia , lookup
Cracking of wireless networks wikipedia , lookup
Piggybacking (Internet access) wikipedia , lookup
Network tap wikipedia , lookup
Airborne Networking wikipedia , lookup
List of wireless community networks by region wikipedia , lookup
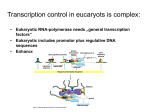
Applications of Random Networks Applications of Random Networks Complex Networks, Course 303A, Spring, 2009 Applications of Random Networks Outline Analysis of real networks Analysis of real networks How to build revisited How to build revisited Motifs Motifs References References Analysis of real networks How to build revisited Motifs Prof. Peter Dodds Department of Mathematics & Statistics University of Vermont References Licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License . More on building random networks I Problem: How much of a real network’s structure is non-random? I Key elephant in the room: the degree distribution Pk . I First observe departure of Pk from a Poisson distribution. I Next: measure the departure of a real network with a degree frequency Nk from a random network with the same degree frequency. I Degree frequency Nk = observed frequency of degrees for a real network. I What we now need to do: Create an ensemble of random networks with degree frequency Nk and then compare. Frame 1/17 Applications of Random Networks Analysis of real networks How to build revisited Motifs References Frame 3/17 Frame 2/17 Building random networks: Stubs Phase 1: I Applications of Random Networks Analysis of real networks Idea: start with a soup of unconnected nodes with stubs (half-edges): I Randomly select stubs (not nodes!) and connect them. I Must have an even number of stubs. I Initially allow self- and repeat connections. How to build revisited Motifs References Frame 5/17 Building random networks: First rewiring Applications of Random Networks Analysis of real networks i2 e1 i1 Analysis of real networks I How to build revisited Motifs Phase 2: I References Now find any (A) self-loops and (B) repeat edges and randomly rewire them. (A) Being careful: we can’t change the degree of any node, so we can’t simply move links around. I Simplest solution: randomly rewire two edges at a time. Sampling random networks e’2 e’1 Applications of Random Networks Check to make sure edges are disjoint. I Rewire one end of each edge. I Node degrees do not change. I Works if e1 is a self-loop or repeated edge. I Same as finding on/off/on/off 4-cycles. and rotating them. i4 i3 (a) How to build revisited Phase 2: I I References I Use rewiring algorithm to remove all self and repeat loops. (b) I Rule of thumb: # Rewirings ' 10 × # edges [?] . 1 configuration 3 90 configurations consists of an out-hub with ten network. The network outgoing edges, an in-hub with ten incoming edges, and ten nodes with one incoming edge and one outgoing edge (c) each. Given this degree sequence, there are just two dis1 tinct network topologies with no multiple edges, as shown in 0.5 Fig. 2a and 2b. There is only a single way to form the with thethere winners network in 2a,gobut are 90 different ways to form 2b. 0 We generated 100 000 random networks using each of 1 the 3 methods described here and the results are summarized in Fig. 2c. As the figure shows, the matching 0.5 switching algorithm algorithm introduces a bias, undersampling the configu0 ration of Fig. 2a. This is a result of the dynamics of the 1 algorithm, which favors the creation of edges between 0.5 hubs. The switching and go-with-the-winners algorithms matching algorithm on the other hand sample the configurations uniformly, 0 generating each graph an equal number of times within FIG. 2:the Uniformity tests of the three algorithms on a toyon net- our calculations. The go-withmeasurement error work. Panels (a) and (b) depict the two types of topologies of IV. CONCLUSIONS the 91 random networks studied, one of them like (a) and 90 the-winners algorithm truly samples the ensemble unilike (b). Panel (c) shows the frequency with which each conIn this paper we have compared three algorithms for figuration is sampled by our three algorithms. 100 000 graphs generating random graphs prescribedmethdegree seformly but is far less efficient than the twowithother were generated with each algorithm, and the figure shows the quences andFrame no multiple9/17 edges or self-edges. Two of the fraction of graphs of each type generated. If sampling were ods. The results given here indicate that the switching three have been used previously, but suffer from nonuni, which is uniform, each should appear with probability formity in their sampling properties, while the third, a indicated by the dotted lines. The go-with-the-winners and algorithm essentially identical while method based on the “goresults with the winners” MontebeCarlo switching algorithms sampleproduces uniformly within sampling error, passing both the Kolmogorov–Smirnoff and Lillie Gausprocedure, is new and provably samples uniformly but sian tests. algorithm under-samples the unique ingTheamatching good deal faster. The ismatching algorithm is faster quite slow. Of the two older algorithms, we show configuration (a). that one, which we call the “matching” algorithm, has still but samples in a measurably way. measurable biased deviations from uniformity when compared Now consider the study of network motifs. We are in1 configuration Frame 8/17 90 configurations 1 91 (c) 1 3 References % frequency of occurrence Randomize network wiring by applying rewiring algorithm liberally. Analysis of real networks Example from Milo et al. (2003) [?] : (a) Frame 7/17 network. The network consists of an out-hub with ten outgoing edges, anto in-hub ten incoming edges, and How buildwith revisited ten nodes with one incoming edge and one outgoing edge each. Given Motifs this degree sequence, there are just two distinct network topologies with no multiple edges, as shown in Fig. 2a and 2b. There is only a single way to form the network in 2a, but there are 90 different ways to form 2b. We generated 100 000 random networks using each of the 3 methods described here and the results are summarized in Fig. 2c. As the figure shows, the matching algorithm introduces a bias, undersampling the configuration of Fig. 2a. This is a result of the dynamics of the algorithm, which favors the creation of edges between hubs. The switching and go-with-the-winners algorithms on the other hand sample the configurations uniformly, generating each graph an equal number of times within the measurement error on our calculations. The go-withthe-winners algorithm truly samples the ensemble uniformly but is far less efficient than the two other methods. The results given here indicate that the switching algorithm produces essentially identical results while being a good deal faster. The matching algorithm is faster still but samples in a measurably biased way. Now consider the study of network motifs. We are interested in knowing when particular subgraphs or motifs appear significantly more or less often in a real-world network than would be expected on the basis of chance, and we can answer this question by comparing motif counts to random graphs. Some results for the case of the “feedforward loop” motif [16, 17] are given in Table I. In this case the densities of motifs in the real-world networks are many standard deviations away from random, which suggests that any of the present algorithms is adequate for generating suitable random graphs to act as a null model, although the go-with-the-winners and switching algorithms, while slower, are clearly more satisfactory theoretically. The matching algorithm was measurably nonuniform for our toy example above, but seems to give better results on the real-world problem. Overall, our results appear to argue in favor of using the switching method, with the go-with-the-winners method finding limited use as a check on the accuracy of sampling. Accuracy checks are also supplied by analytical estimates for subgraph numbers [11]. (b) Problem with only joining up stubs is failure to randomly sample from all possible networks. Phase 3: I Motifs References Applications of Random Networks Random sampling Analysis of real networks Motifs How to build revisited i2 i1 Frame 6/17 Randomly choose two edges. (Or choose problem edge and a random edge) I i4 e2 i3 (B) I Applications of Random Networks General random rewiring algorithm Sampling random networks Applications of Random Networks Analysis of real networks I Motifs I Must now create nodes before start of the construction algorithm. I Generate N nodes by sampling from degree distribution Pk . I Easy to do exactly numerically since k is discrete. I Note: not all Pk will always give nodes that can be wired together. letter References I Applications of Random Networks n crp araC araBAD c single input module (SIM) b c I e n doors. Analogy Z1 Z2 to...elevator Zn We compiled a data set of direct transcriptional interactions occur in various organisms, such as the genetic switch in argI argF argE argD argCBH n single input module (SIM) X Z1 Z2 X ... Zn n d Turning of X rapidlyX turns of Z . dense overlapping regulons (DOR) Z crp Little is known about the design principles1–10 of transcripHow to build revisited tional regulation networks that control gene expression Motifs in 2,11,12 2 Dynamic , features of the coherent feedforward loop and SIM acells. Recent advances in data collection and analysisFig. motifs. a, Consider a coherent feedforward loop circuit with an ‘ANDhowever, are generating unprecedented amounts of informaReferences gate’–like control of the output operon Z. This circuit can reject rapid in the activity of the input X, and respond only to persistent tion about gene regulation networks. To understandvariations these activation profiles. This is because Y needs to integrate the input X oversuch time to pass the activation threshold for Z (thin line). A similar complex wiring diagrams1–10,13, we sought to break down rejection of rapid fluctuations can be achieved by a cascade, X#Y#Z; networks into basic building blocks2. We generalize the however, notionthe cascade has a slower shut-down than the feedforward loop (thin red line in the Z dynamics panel). b, Dynamics of the SIM of motifs, widely used for sequence analysis, to the level of motif. This motif can show a temporal program of expression according to a hierarchy of activation thresholds of the genes. When the networks. We define ‘network motifs’ as patterns of interconactivity of X, the master activator, rises and falls with time, the genes nections that recur in many different parts of a networkwith at the fre-lowest threshold are activated earliest and deactivated latest. Time is in units of protein lifetimes, or of cell cycles in the case of quencies much higher than those found in randomized long-lived proteins. networks. We applied new algorithms for systematically detecting network motifs to one of the best-characterized reg3, usually involving !-factors, such as caslong cascades ulation networks, that of direct transcriptional interactions in cades of depth 5 in the flagella and nitrogen systems. Over Escherichia coli3,6. We find that much of the network is com70% of the operons are connected to the DORs; the rest of the operons are in small disjoint systems. Most disjoint bposed of repeated appearances of three highly significant motifs. Each network motif has a specific function in determinsystems have only 1 to 3 operons. The remaining disjoint systems have up to 25 operons and show many SIMs and ing gene expression, such as generating temporal expression feedforward loops. A notable feature of the overall organiprograms and governing the responses to fluctuating external zation is the large degree of overlap within DORs between signals. The motif structure also allows an easily interpretable the short cascades that control most operons. The layer of may therefore represent the core of the computaview of the entire known transcriptional network of the DORs organtion carried out by the transcriptional network. ism. This approach may help define the basic computational Cycles such as feedback loops are an important feature elements of other biological networks. of regulatory networks. Transcriptional feedback loops I argR Y araBAD Z only turns on in response to sustained activity in X . d Y Network motifsaraC I X e X "-phage between transcription factors and the operons they regulate (an5. In the E. coli data set, there are no examples of operon is a group of contiguous genes that are transcribedfeedback into a loops of direct transcriptional interactions, except for auto-regulatory loops3. However, the absence single databaseof Xcontains interacfrom X andmRNA a delayedmolecule). one through Y.This If the activation is tran- of577 feedback loops is not statistically significant, as over 80% of tions and 424 (involving 116 transcription randomizeditnetworks also have no feedback loops (Table 1). sient, Y cannot reachoperons the level needed to significantly activate Z, the factors); and the formed input signalon is not theexisting circuit. Only The many regulatory Framefeedbacks 13/17 loops in the organism are carried was thetransduced basis ofthrough on an database (Reguwhen X signals a long enough time so that Y levels can build out at the post-transcriptional level. lonDB)3,14.forWe enhanced RegulonDB by an extensive literature We considered only transcription interactions specifically up will Z be activated (Fig. 2a). Once X is deactivated, Z shuts search, adding 35 new transcription factors, including alternadown rapidly. This kind of behavior can be useful for making manifested by transcription factors that bind regulatory sites3,14. decisions based on fluctuating signals. This transcriptional tive !-factors (subunitsexternal of RNA polymerase that confer recogni- network can be thought of as the ‘slow’ part The SIM is found in systemssequences). of genes that function sto- set of the cellularof regulation network (time scale of minutes). An tion of motif specific promoter The data consists chiometrically to form a protein assembly (such as flagella) or a additional layer of faster interactions, which include interactions established interactions in which a transcription factor directly argR argI Z Looked for certain subnetworks (motifs)Little thatis known about the design principles feedforward loop tional regulation networks that control ge appeared more or less often than expected cells. Recent advances in data collection a X however, are generating unprecedented amo argF Y © 2002 Nature Publishing Group http://genetics.nature.com b X Y I argE X a argD feedforward loop Analysis of real networks produce ensemble of alternate networks with same degree frequency Nk . argCBH a Specific example of Escherichia coli. Published online: 22 April 2002, DOI: 10.1038/ng881to I Used network randomization Published online: 22 April 2002, DOI: 10.1038/ng881 letter Motifs References 424 operons (nodes). Network motifs in the transcriptional regulation network of Escherichia coli Network motifs How to build revisited I Shen-Orr 1, Ron 1 & Uri(edges) Directed network 577 Mangan interactions Shai S. Milo2,with Shmoolik Alon1,2 and Frame 10/17 Shai S. Shen-Orr1, Ron Milo2, Shmoolik Mangan1 & Uri Alon1,2 Idea of motifs [?] introduced by Shen-Orr, Alon et al. in 2002. I Looked at Network motifs in thewithin transcriptional regulation gene expression full context of transcriptional regulation networks. network of Escherichia coli © 2002 Nature Publishing Group http://genetics.nature.com What if we have Pk instead of Nk ? Analysis of real networks letter How to build revisited I Applications of Random Networks Network motifs dense overlapping regulons (DOR) I Master switch. X1 X2 X3 ... Z1 Z2 Xn Z3 Z4 ... Zm X1 X2 X3 Xn tion about gene regulation networks. To u 1–10,1312/17 complex wiring diagramsFrame , we sought to networks into basic building blocks2. We gene of motifs, widely used for sequence analysi networks. We define ‘network motifs’ as pat nections that recur in many different parts of quencies much higher than those found networks. We applied new algorithms fo Applications of best-c detecting network motifs to one of the Random Networks ulation networks, that of direct transcription Escherichia coli3,6. We find that much of the posed of repeated appearances of three h Analysis of real networks motifs. Each network motif has a specific func to build revisited ing gene expression, suchHowas generating tem Motifs programs and governing the responses to flu References signals. The motif structure also allows an ea view of the entire known transcriptional netw ism. This approach may help define the bas elements of other biological networks. We compiled a data set of direct transcripti between transcription factors and the operons operon is a group of contiguous genes that are single mRNA molecule). This database cont tions and 424 operons (involving 116 transcr was formed on the basis of on an existing lonDB)3,14. We enhanced RegulonDB by an ex search, adding 35 new transcription factors, i tive !-factors (subunits of RNA polymerase th tion of specific promoter sequences). The da established interactions in which a transcripti binds a regulatory site. The transcriptional network can be represe graph, in which each node represents an operon Frame 14/17 sent direct transcriptional interactions. Each Fig. 1 Network motifs found in the E. coli transcriptiona Symbols representing the motifs are also shown. a, Feed d argR argI argF argE ... Xn X1 X2 X3 Xn Analysis of real networks How to build revisited Motifs References fis crp nhaR Fig. 1 Network motifs found in the E. coli transcriptional regulation network. Symbols representing the motifs are also shown. a, Feedforward loop: a I transcription factor X regulates a second transcription factor Y, and both jointly regulate one or more operons Z1...Zn. b, Example of a feedforward loop (L-arabinose utilization). c, SIM motif: a single transcription factor, X, regulates a set of operons Z1...Zn. X is usually autoregulatory. All regulations are of the same sign. No other transcription factor regulates the operons. d, Example of a SIM system (arginine biosynthesis). e, DOR motif: a set of operons Z1...Zm are each regulated by a combination of a set of input transcription factors, X1...Xn. DORs are defined by an algorithm that detects dense regions of connections, with a high ratio of connections to transcription factors. f, Example of a DOR (stationary phase response). For more, see work carried out by Wiggins et al. at Columbia. proP nhaA hns ftsQAZ rcsA lrp osmC Applications of Random Networks selection of motifs to test is reasonable but nevertheless ad-hoc. Z3 Z4 ... Zm ihf alkA ada Z2 rpoS Z1 X3 oxyR X2 dps X1 f Network motifs dense overlapping regulons (DOR) katG e argD argCBH Network motifs between transcription factors and the operons they regulate (an operon is a group of contiguous genes that are transcribed into a single mRNA molecule). This database contains 577 interacApplications of tions and 424 operons (involving 116 transcription factors); it Random Networks was formed on the basis of on an existing database (RegulonDB)3,14. We enhanced RegulonDB by an extensive literature search, adding 35 new transcription factors, including alternaAnalysis of real tive !-factors (subunits of RNA polymerase that confer recogninetworks How to build revisitedThe data set consists of tion of specific promoter sequences). Motifs established interactions in which a transcription factor directly References binds a regulatory site. The transcriptional network can be represented as a directed graph, in which each node represents an operon and edges represent direct transcriptional interactions. Each edge is directed I Note: 1Department of Molecular Cell Biology, 2Department of Physics of Complex Systems, Weizmann Institute of Science, Rehovot 76100, Israel. Correspondence should be addressed to U.A. (e-mail: [email protected]). 64 References I Frame 15/17 nature genetics • volume 31 • may 2002 Applications of Random Networks Analysis of real networks How to build revisited Motifs References Frame 17/17 Frame 16/17