* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download [download PDF ]
Survey
Document related concepts
Transcript
Tectonophysics 510 (2011) 69–79
Contents lists available at ScienceDirect
Tectonophysics
j o u r n a l h o m e p a g e : w w w. e l s ev i e r. c o m / l o c a t e / t e c t o
Mechanical twinning in quartz: Shock experiments, impact, pseudotachylites and
fault breccias
Hans-Rudolf Wenk a,⁎, Christoph Janssen b, Thomas Kenkmann c, Georg Dresen b
a
b
c
Department of Earth and Planetary Science, University of California, Berkeley, CA 94720, USA
GFZ German Research Centre for Geosciences, Telegrafenberg, 14473 Potsdam, Germany
Institut für Geowissenschaften, Geologie, Albert-Ludwigs-Universität, 79085 Freiburg, Germany
a r t i c l e
i n f o
Article history:
Received 19 March 2011
Received in revised form 14 June 2011
Accepted 17 June 2011
Available online 28 June 2011
Keywords:
Quartz
Dauphiné twinning
Shock deformation
Seismic stress
Pseudotachylites
EBSD
a b s t r a c t
Increasing use of diffraction methods to study preferred orientation of minerals has established that quartz in
deformed rocks not only displays characteristic c-axis orientation patterns, but that there is also generally a
distinct difference in the orientation of positive and negative rhombs. In the trigonal quartz crystal structure
positive and negative rhombs are structurally different, and particularly negative rhombs (e.g. {0111}) are
much stiffer than positive rhombs (e.g. {1011}). Here, we focus on the role of mechanical Dauphiné twinning
under stress as a cause of this difference and illustrate with EBSD measurements ubiquitous twinning in
quartz-bearing rocks subjected to high stresses. Characteristic twinning is observed in experimentally
shocked sandstones and stishovite-bearing quartzites from the Vredefort meteorite impact site in South
Africa. Similar twinning is documented for quartz associated with pseudotachylites from the Santa Rosa
mylonite zone in Southern California, whereas quartz in underlying ductile mylonites are more or less twinfree. It suggests that twinning was produced by local seismic stresses that caused fracture and frictional
melting on fault surfaces. Quartz-bearing breccias from the SAFOD (San Andreas Fault Observatory at Depth)
drilling project also show evidence of twinning and suggest high seismic stresses in the currently creeping
segment of the San Andreas Fault at Parkfield. From these observations it appears that Dauphiné twin
microstructures can be diagnostic of high local and transient stresses.
© 2011 Elsevier B.V. All rights reserved.
1. Introduction
It has long been known that quartz undergoes mechanical twinning
when exposed to high stresses (Schubnikov, 1930; Schubnikov and
Zinserling, 1932). The significance of these twins in deformed quartz
aggregates was first investigated by Tullis (1970) and Tullis and Tullis
(1972). Mechanical twins occur in many materials (e.g., KlassenNeklyudova, 1964) but Dauphiné twins in quartz are rather special
compared, for example, with classical twins in carbonates (e.g. Barber
and Wenk, 1979; Pfaff, 1859) or hexagonal metals (e.g. Partridge, 1967;
Yoo, 1981). The twin–host relationship for Dauphiné twins is a 180°
rotation about the c-axis of trigonal quartz. On the atomic scale, it is
achieved by a slight distortion of the structure (Fig. 1), without
significant change in macroscopic shape of the quartz crystal. Twinning
does not change the orientation of the c-axis or a-axes but reverses
positive rhombs such as {1011} and negative rhombs {0111}. This is of
profound mechanical importance, as directions normal to positive
rhombs are half as stiff as those normal to negative rhombs (e.g.,
McSkimin et al., 1965). In a compression experiment with a quartz
⁎ Corresponding author. Fax: + 1 510 643 9980.
E-mail address: [email protected] (H.-R. Wenk).
0040-1951/$ – see front matter © 2011 Elsevier B.V. All rights reserved.
doi:10.1016/j.tecto.2011.06.016
aggregate, crystals with normal to negative rhombs parallel to the
compression direction will become twinned, resulting in a new
orientation with poles of positive rhombs parallel to the compression
direction. In situ neutron diffraction experiments indicate that twinning
initiates at 50–100 MPa and that activation of twinning is temperaturedependent (Wenk et al., 2006, 2007).
Dauphiné twinning is expressed in the bulk preferred orientation
of quartz crystals in a rock. If the orientation of c-axes and a-axes is
random, but positive and negative rhombs show an inverse pattern
with corresponding minima and maxima, then it is likely that this
pattern was produced by twinning; but the volume fractions of twins
and hosts must be different (e.g. Tullis, 1970). If positive and negative
rhombs show the same orientation distribution (i.e., identical pole
figures), this could be interpreted as grains that are divided into equal
fractions of host and twin domains. It could also be due to a statistical
distribution of untwinned grains in one orientation and another
orientation related to the first orientation by a 180° rotation about the
c-axis. For most metamorphic quartzites pole figures of positive and
negative rhombs are distinctly different (e.g., Baker and Wenk, 1972;
Pehl and Wenk, 2005; Wenk et al., 2009, 2010). This precludes a large
fraction of twins in individual grains.
The actual presence of twins needs to be investigated at the
microstructural scale. Contrary to calcite twins, Dauphiné twins cannot
70
H.-R. Wenk et al. / Tectonophysics 510 (2011) 69–79
Fig. 1. Schematic structure of a mechanical Dauphiné twin, produced by shear. [0001]
projection. Twin plane is horizontal and sense of shear is indicated. Only Si atoms are
shown with gray shades for different z-coordinates. Trigonal distortion is exaggerated
(from Schubnikov and Zinserling, 1932).
be detected with a petrographic microscope, due to the coincidence
of c-axes between twin and host. Thus, either transmission (e.g.,
Barber and Wenk, 1991) or scanning electron microscopy (e.g., Lloyd,
2000, 2004; Trimby et al., 1998) is required to image them. The
electron backscatter diffraction (EBSD) technique is most suitable
and has been first applied by Heidelbach et al. (2000) to map twin
boundaries in metamorphic quartz. This is the method which we will
apply in this study.
There is no doubt that Dauphiné twins in quartz can be produced
under tectonic conditions, just as calcite twins form in metamorphic
marbles. It has also been established that twins develop during the
β–α phase transformation (Van Tendeloo et al., 1976). Here, we are
focusing on quartz in rocks that were subjected to high local dynamic
stresses, such as in shock experiments, meteorite impacts and seismic
events.
2. Methods
From rock slabs 30 μm thick petrographic thin sections were
prepared and subsequently polished. First a 3 μm diamond polish was
applied for roughly 2 h, then a 1/4 μm diamond polish for half an hour,
and finally the sample was polished for 5 min by hand with colloidal
silica. No coating was applied to the sample.
The thin section was first investigated with a petrographic
microscope to identify regions of interest. Then selected regions were
studied in a Zeiss EVO MA10 scanning electron microscope (SEM) at
25 kV, 100 μA beam current, 5 nA I Probe current, 10 Pa variable
pressure vacuum to avoid charging, and a working distance of 18–
25 mm. The sample surface was tilted 70˚ relative to the horizontal.
Diffraction patterns were recorded with a Digiview IV high resolution
digital camera. Data collection and pattern indexing was performed
with the TSL-OIM software. Images with 1024 × 1024 resolution were
binned 2 × 2 or 4 × 4. Scans were performed over rectangular regions of
200–300 μm in 1 μm steps. Such a fine step size is necessary to resolve
the twin boundaries satisfactorily. A scan usually took about 24 h.
Indexing of trigonal quartz is not trivial. Identification of the trigonal
orientation relies on intensity differences between diffractions of
positive and negative rhombs. Contrary to calcite, where rhombohedral
space group symmetry causes systematic extinctions for unambiguous
indexing, in quartz both positive and negative rhombs diffract at the
same Bragg angle, though with different intensity. The intensity
differences rely on the crystal structure, and hereby further confusion
may occur for quartz. Traditionally {1011} is the morphologically
dominant rhomb (e.g., Frondel, 1962; Goldschmidt, 1897; Hauy, 1801).
This setting for the unit cell was used by Gibbs (1926) for the description
of the crystal structure in space group P3121, and it follows that for X-ray
and electron diffraction the following intensity relationships exists
between positive and negative rhombs: 1011 N 0111, 1012 b 0112,
2011 b 0211, 2022 N 0222, 1013 N 0113. Unfortunately, some later descriptions of the quartz crystal structure have not followed this
convention (e.g., discussion by Heaney et al., 1994, p 8) which is critical
for an unequivocal definition of crystal orientation, as well as regarding
physical properties such as elasticity.
Before entering a quartz structure into EBSD indexing software it is
necessary to carefully check reflectors. Mostly EBSD systems do not
discriminate intensity and, thus, only the more intense rhombohedral
reflections should be used for indexing. Fig. 2 shows two diffraction
patterns which are related by Dauphiné twinning. Note that most
lines are identical. They define the geometry of the hexagonal unit
cell. A few lines are different in intensity and one is indicated by
arrows. If image quality is low, there is a fair probability that automatic indexing chooses the wrong orientation, resulting in individual
spots which are related by the twin orientation.
We describe the procedure in some detail for a quartz crystal from
the Vredefort impact site which will be described later in more detail.
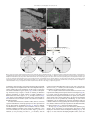
Fig. 3a shows an optical micrograph of a grain with parallel deformation
lamellae that was selected in a thin section. The SEM image with
backscattered electron (BE) contrast (collected with the forward
scattering detector on the tilted sample) (Fig. 3b) displays surface
Fig. 2. EBSD diffraction patterns of quartz from two domains related by Dauphiné twinning. Note that only some bands are different. Arrows point towards corresponding band of
trigonal reflections with different intensity.
H.-R. Wenk et al. / Tectonophysics 510 (2011) 69–79
71
Fig. 3. Quartz crystal from stishovite-bearing quartzite near Weltevrede farm in theVredefort dome. (a) Optical micrograph showing deformation lamellae, crossed polarizers.
(b) SEM forward scattering image, of which an area was selected for a detailed EBSD scan (green outline). (c) EBSD scan in 0.5 μm steps with a map of Euler angle ϕ2. Note that some
Dauphiné twin boundaries (red) are parallel to deformation lamellae. The corresponding gray-shade scale is shown to the lower right and applies to all subsequent orientation maps
as well. (d) Histogram of misorientation versus ϕ2 with a sharp peak at 60°, corresponding to the 60° rotation about the c-axis which relates twin and host. (e) Pole figures of twin
and host with a single c-axis maximum (determined by Euler angles ϕ1 Φ) and 103 as well as 013 pole figures. The diffraction peak intensities (arrows, pole densities in multiples of a
random distribution—m.r.d.) correspond to the volume fractions of host and twin in the image (c). Equal area projection.
morphology (with some holes) and contrast variations that are partially
due to the presence of Dauphiné twins. BE contrast depends mainly on
atomic number and crystal orientation. On this image a region was
selected for a detailed scan (green square). Fig. 3c shows a corresponding orientation map of angle ϕ2. Based on indexing of diffraction
patterns, orientations of crystals relative to sample coordinates are
defined with three Euler angles ϕ1,Φ, ϕ2 (in Bunge notation, Bunge,
1965). Angles ϕ1 and Φ define the orientation of the c-axis and angle ϕ2
the rotation of a-axes around the crystal c-axis and is thus sensitive to
Dauphiné twinning.
Scan data with orientations, confidence index, which is a measure
of pattern identification, and image quality were then exported from
the TSL-OIM software to BEARTEX (Wenk et al., 1998) for mapping
and identification of Dauphiné twin boundaries with the routine
MAPTEX. Dauphiné boundaries must satisfy two conditions: c-axes
across the boundary are the same, thus Euler angles ϕ1 and Φ are
identical (In our processing we allow a ±2° variation) and the
rotation around c defined by Euler angle ϕ2 is 60° (180°) (also here we
allow for a 60° ± 2° variation). If both conditions are satisfied, twin
boundaries are plotted as red lines on the maps.
We can compile misorientation statistics between each cell on the
map and surrounding cells and represent them on a histogram (Fig. 3d).
For a single crystal all misorientations are close to zero with small
deviations due to subgrain misorientations. For quartz, there is almost
always a peak at 60°, which is partly due to the presence of Dauphiné
twins but can also be produced by misindexing. To some extent
misindexing can be minimized by rejecting orientations with low
confidence index or low image quality, but we need to keep in mind that
the confidence index is based only on positions of the diffraction bands,
not their intensity (Fig. 2)—and some ambiguity remains.
The map (Fig. 3c) clearly shows two orientations (different gray
shades). These orientations are represented in pole figures, which
display two orientations related to Dauphiné twinning (Fig. 3e). The
angle ϕ2 is most critical for identifying Dauphiné twins, as the two
72
H.-R. Wenk et al. / Tectonophysics 510 (2011) 69–79
domains are related by a ϕ2 = 60° (180°–120°) angle. The poles of
(1013) for the host correspond to the poles of (0113) of the twin. The
pole density for the host is higher (43 multiples of a random
distribution, m.r.d.) than that of the twin (25 m.r.d.), indicating that
about 60% of the surface of Fig. 3c is host (dark) and 40% twin (light).
A few grains were scanned in each sample to establish consistency.
Not all the data can be shown. Clearly, what is presented here is not a
statistical result and we have not even attempted to quantify twin
fractions in grains or relationships between twins and grain
orientation, but the results obtained so far appeared to us convincing
enough to support our conclusions.
For two samples, a granitic breccia from the Nördlinger Ries and a
metamorphic quartzite from the Bergell Alps, we also display pole
figures to illustrate bulk preferred orientation, especially the difference
between positive and negative rhombs. Textures have been measured
on 1 cm cubes by time-of-flight neutron diffraction with the HIPPO
diffractometer at Los Alamos (Wenk et al., 2010).
3. Results
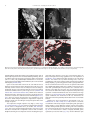
3.1. Experimentally Shocked Sandstone
The first sample that was investigated is a porous sandstone
(Seeberger Sandstein, from Gotha, Germany, Seidel, 1992) that underwent shock-loading. Cratering experiments were performed at the twostage light-gas acceleration facility at Fraunhofer Ernst-Mach-Institute
in Efringen-Kirchen, Germany, as part of the MEMIN program (Multidisciplinary Experimental and Modeling Impact Research Network,
Kenkmann et al., 2011). MEMIN focuses on impact cratering experiments in geological materials to comprehensively understand details of
the cratering process through in situ measurements, extensive postimpact analysis, and numerical modeling. The investigated sample
stems from a calibration test shot in which a 1 cm steel projectile
weighing 4.1 g was accelerated horizontally to ~4500 m s − 1 and
impacted onto the flat, vertical surface of a 40 cm cube of Seeberger
sandstone. The kinetic energy of the experiment was 41.5 kJ and the
expected peak shock pressures were 50–55 GPa at the contact of the
projectile with the target. The crater volume was ~620 cm3. However,
impact-induced fractures reached the edges and completely disjointed
the target cube.
The 20 × 15 × 2 cm sample investigated here contains the crater
floor. Some material around the projectile impact was partly
pulverized and ejected. As the shock pressure rapidly decays in
porous targets with increasing distance from the point of impact, the
assumed shock pressure in the sample is estimated to be of the order
of a few GPa.
An optical examination of the thin section reveals rounded and
slightly flattened grains of quartz with interstitial phyllosilicates
(Fig. 4a). There are no obvious deformation features such as planar
deformation lamellae in quartz. EBSD scans were performed on
several grains from about 4 cm beneath the central crater floor and on
grains immediately on the crater floor. Grains from the subsurface are
Fig. 4. Seeberger sandstone, experimentally shock-deformed within the MEMIN project. (a) Microstructure viewed with a petrographic microscope, crossed polarizers. (b-d) EBSD
maps of Euler angle ϕ2, 1 μm steps. Dauphiné twin boundaries are red. In material distant (20 mm) from the point of projectile impact, grains are largely uniform (b). Some
boundaries coinciding with grain boundaries may be artifacts of misindexing. (c, d) Near the point of impact grains display Dauphiné twinning, particularly near grain boundaries
and at edges of grains. White regions could not be indexed or were rejected because of poor confidence index, or because they represent other phases between quartz grains.
H.-R. Wenk et al. / Tectonophysics 510 (2011) 69–79
uniform with only occasional twin boundaries (Fig. 4b). Grains in the
impact region clearly show an abundance of twins, particularly at the
margins of grains and on surfaces where two quartz grains are in
direct contact (Fig. 4c,d). Some grains are more intensively twinned
than others, which could be related to the relation between shock
wave direction and crystal orientation.
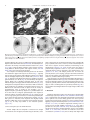
3.2. Quartz Deformed During Meteorite Impact
Based on preferred orientation patterns of quartz it was suggested
that shock stresses may have caused Dauphiné twinning in stishovitebearing quartzites from the Vredefort impact site in South Africa (Wenk
et al., 2005). This was recently confirmed by EBSD measurements (Chen
et al., 2011). Here, we reinvestigate microstructures in the same sample
from Weltevrede farm northeast of Parys, about 30 km northeast of the
impact center (Gibson et al., 1997). Dauphiné twins occur in grains that
are oriented with the c-axis in the plane of the section (Figs. 3a, 5a) and
the c-axis perpendicular to the thin section (Fig. 5b). Figs. 3a and 5a
display deformation lamellae oriented at high angles to the c-axis.
Orientation mapping clearly shows abundant twins with dominant twin
boundaries that are parallel to the deformation lamellae (Figs. 3c, 5c).
This suggests a close relationship between the two microstructures. The
lamellae are subparallel to {1013} or {0113} (Fig. 3e, Trepmann and
Spray, 2005; Vernooij and Langenhorst, 2005). Dauphiné twinning
resolves this puzzling relationship with equivalent positive and negative
rhombs: a boundary that is parallel to a positive rhomb in the host is also
parallel to the adjacent negative rhomb in the twin. In grains viewed
along the c-axis (Fig. 5b) no such relationship is evident. Also, there are
abundant twins here (Fig. 5d). The domains are larger and less regular,
though some boundaries display approximate 120° / 60° angles (arrow).
73
A second natural impact sample investigated originates from the
Ries impact structure (sample 2008-02385 from the Museum für
Naturkunde, Berlin). The “granite breccia” from W of the town of
Schmähingen consists of coherent granitic fragments in a more finegrained matrix of the same material (Von Engelhardt, 1974). The
fragments are rotated; we analyzed the microstructure of one of the
fragments (our label R8). In the thin section we can see elongated
quartz grains (Fig. 6a). Texture analysis with the HIPPO neutron timeof-flight diffractometer establishes a strong preferred orientation of
c-axes (Fig. 6c), with a c-axis maximum exceeding 6 multiples of a
random distribution and distinct differences between positive
rhombs {1011} and negative rhombs {0111}. The c-axis pattern is
clearly not caused by impact and the rock represents a foliated gneiss
rather than a granite and has undergone extensive ductile deformation. However, the orientation of the rhombs may be related to the
impact. Note that in pole figures of the positive rhomb {1011}
subsidiary concentrations corresponding to maxima of the negative
rhomb {0111}, are indicated by arrows (Fig. 6c). This is likely
evidence for reorientation by partial twinning. Quartz grains in this
Ries sample do not display visible deformation lamellae (Fig. 6a),
suggesting lower stresses than in the case of Vredefort. EBSD maps
nevertheless display abundant twinning (Fig. 6b).
3.3. Quartz Associated with Pseudotachylites
Having established that Dauphiné twins are common in shockdeformed materials, we wanted to explore whether stresses generated
during seismic events could induce similar features. Obvious rocks to
investigate are pseudotachylites that are thought to have originated by
frictional melting during seismic rupture (Sibson, 1975). We explored
twinning in quartz-bearing rocks from the Santa Rosa mylonite zone in
Fig. 5. Vredefort quartzite from Weltevrede farm. (a,c): Grain viewed perpendicular to the c-axis shows deformation lamellae. (b,d): Grain viewed parallel to c-axis. (a,b) Optical
photomicrographs with crossed polarizers. (c,d) EBSD maps of Euler angle ϕ2, 1 μm steps. Dauphiné twin boundaries shown in red. Note the clear morphologic relationship between
deformation lamellae (a) and twin boundaries (c). Arrow in (d) points to an approximate 120˚ angle at a twin boundary.
74
H.-R. Wenk et al. / Tectonophysics 510 (2011) 69–79
Fig. 6. Quartz in granitic breccia R8 from Schmähingen, Nördlinger Ries. (a) Optical photomicrograph (plane polarized light) illustrating deformed quartz grains. (b) EBSD map of a
grain, illustrating a few Dauphiné twin boundaries. (c) Pole figures measured by neutron diffraction, displaying very strong preferred orientation with a pattern close to that of a
single crystal. Arrows in (1011) pole figure point at subsidiary maxima, corresponding to principal maxima of the negative rhomb (0111). Equal area projection. Linear contour
levels in multiples of a random distribution.
Southern California. Here, there is a gradient from ductile mylonites at
depth to brittle deformation above (Wenk, 1998). Pseudotachylites are
observed in the vicinity of the brittle–ductile transition zone (Wenk
et al., 2000). In largely ductile mylonites, texture analysis reveals a
strong difference between positive and negative rhombs (Pehl and
Wenk, 2005). Thus, twins cannot be prevalent.
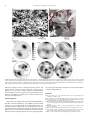
Two examples of moderately deformed granite from the ductile
zone obtained in upper Palm Canyon are shown in Fig. 7. Typically
there are large grains of quartz with undulatory extinction, as in PC 89
that was investigated previously for residual strain (Kunz et al., 2009)
(Fig. 7a). With increasing deformation quartz recrystallizes, first along
grain boundaries as in PC 88 (Fig. 7b), and ultimately throughout a
sample. EBSD scans of ductilely deformed quartz in both rocks
indicate that grains are largely uniform and devoid of twins (Fig. 7c,d),
although there are slight variations in orientation, visible as variations
in gray shades that are indicative of subgrain formation. This is very
different from observations made on quartz from the vicinity of
pseudotachylite veins, as shown by two examples: one is a
fragmented quartz grain directly adjacent to a pseudotachylite vein
in PC 825 from the contiguous pseudotachylite zone exposed at
elevation 1900 ft E of Martinez Mountain (Fig. 8a), and the second
one is a large quartz grain from about 2 cm from the pseudotachylite
in PC 738c from Deep Canyon SE of Black Hill (at 3000 ft) (Fig. 8b).
Both grains are fractured, with misplaced and slightly rotated
fragments. EBSD maps reveal a profusion of twin domain structures
(Fig. 8 c,d), in many ways similar to the Vredefort quartzite
(Figs. 3c, 5c).
3.4. Brecciated Quartz from the SAFOD Drill Hole
Another sample that was analyzed is a fractured core sample
recovered from 3141 m depth (measured along the borehole) of the
phase 3 borehole of the San Andreas Fault Observatory at Depth ICDP
project (SAFOD; Hole E, Run 1, Section 6). This brecciated sample was
taken from a sequence of arkosic sandstone, which belongs to the
Salinian Block (Springer et al., 2009). In thin section, the matrix is
predominantly composed of coarse- to very coarse, subrounded to
subangular quartz (36 wt.%), plagioclase (22%) and microcline (17%)
(Janssen et al., 2011). The sample position was 16 m from the
presently inactive (non-creeping) ‘geological’ San Andreas Fault that
forms the eastern limit of the Salinian Block and 50 m from the active
fault trace (southwest deforming zone/SDZ).
Large quartz grains are often fractured with displaced fragments in a
fine-grained cataclastic matrix (Fig. 9a,b). Some of these quartz clusters
have been analyzed in detail. A very interesting pattern emerges: large
crystals are generally uniform, without much twinning, but corners and
edges, as well as small fragments are pervasively twinned (Fig. 9b,c).
Stresses which caused fragmentation were high enough to induce local
twinning.
4. Discussion
Mechanical twinning in quartz was discovered in experimentally
stressed single crystals (Schubnikov, 1930; Schubnikov and Zinserling,
1932). Localized twins were produced by mechanical action with steel
pins or spheres. Later, stresses during growth were used to prevent
growth twins in piezoelectric material or to remove existing twins by
applying a torque at elevated temperature (Thomas and Wooster, 1951;
Wooster et al., 1947). At ambient temperature twinning occurs at
average stresses around 500 MPa (Bertagnolli et al., 1979) and is
pervasive at 1 GPa (Tullis and Tullis, 1972). At elevated temperatures
and pressures twinning is already initiated at stresses of 50–200 MPa
(Wenk et al., 2006, 2007). But twins are induced at local stress
concentrations (Schubnikov, 1930) that are likely much higher than
H.-R. Wenk et al. / Tectonophysics 510 (2011) 69–79
75
Fig. 7. Moderately deformed granite from Palm Canyon in the Santa Rosa mylonite zone in Southern California. (a,c): Sample PC 89. (b,d): Sample PC 88. (a,b) Optical
photomicrographs taken with crossed polarizers. (c,d) EBSD maps of Euler angle ϕ2. Dauphiné twin boundaries are shown in red. (a) The large quartz grain shows undulatory
extinction due to moderate plastic deformation. (b) In this sample, quartz has become recrystallized along grain boundaries. (c,d) In both samples division into subgrains (variation
in gray shades) is noted, but Dauphiné twins are largely absent.
average stresses. The experimentally shocked sandstone was subjected
to stresses up to 50–55 GPa. (Kenkmann et al., 2011). However, the
coherent material studied here, contrary to ejected fragments, represents much lower shock stresses, presumably 3–5 GPa.
Typical features in quartz, experimentally shocked below 8–
10 GPa, are planar shock lamellae (e.g., Gratz et al., 1988, 1992;
Stöffler and Langenhorst, 1994). Such lamellar structures are not
restricted to shock deformation but are also produced in conventional
deformation experiments at elevated pressures and temperatures
(e.g. Vernooij and Langenhorst, 2005) and observed in metamorphic
rocks. As we have shown in Fig. 5c, these lamellae are closely linked to
Dauphiné twins, at least in Vredefort quartzite. The morphology, with
twin boundaries parallel to the rhombohedral lamellae, explains why
the lamellae are either of {1013} or {0113} orientations. In this sample
there is no evidence for amorphous zones or high dislocation densities
along lamellar boundaries, but obviously the EBSD resolution is not at
the nanometer scale. The close geometric relationship between
lamellae and twin boundaries suggests that the two features were
produced simultaneously.
Dauphiné twinning is pervasive in quartz rocks subjected to
meteorite impact. Apart from Vredefort and Ries, it has been
documented for the Charlevoix impact structure in Canada (Trepmann
and Spray, 2005) and the Rochechouart impact in France (Trepmann,
2008). Shock pressures for their production are above the Hugoniot
elastic limit and have been estimated at N3–8 GPa (Stöffler and
Langenhorst, 1994). This is consistent with the partial conversion of
quartz to stishovite in the Vredefort quartzite (Martini, 1978) which also
suggests pressures N7 GPa.
While twinning in quartz subjected to meteorite impact is well
established, it has been surprising to find similar microstructures in
rocks exposed to seismic stresses. For this a survey through the brittle–
ductile transition in the Santa Rosa mylonite zone in Southern California
has been most revealing. Quartz in granitic rocks from the ductile
deformation zone, also associated with sillimanite and cordieritebearing paragneisses and tremolite-bearing marbles, shows signs of
plastic deformation such as undulatory extinction, grain flattening and
recrystallization. This implies high temperatures and low stresses. In
such rocks Dauphiné twins are largely absent. This situation changes as
one passes the brittle–ductile transition zone, with a distinct zone of
pseudotachylites that can be attributed to ancient seismic activity. If one
accepts the hypothesis that these enigmatic rocks are produced by
frictional melting on ruptured fault surfaces (Sibson, 1975), then
stresses had to exceed the shear strength of the rocks. Local stress
concentrations had to be higher than the shear strength of quartz to
produce extensive failure. Quartz is one of the strongest components
of gneisses. There is abundant twinning in quartz associated with
76
H.-R. Wenk et al. / Tectonophysics 510 (2011) 69–79
Fig. 8. Quartz associated with pseudotachylite from the Santa Rosa mylonite zone. (a,c): Sample PC 825, Martinez Mountain. (b,d): Sample PC 738c, Deep Canyon. (a,b) Photomicrographs
taken with crossed polarizers, illustrating fractured quartz grains. (c,d) EBSD maps of Euler angle ϕ2, 1 μm steps. Dauphiné twins (boundaries are red) occur pervasively.
pseudotachylites. If frictional melting occurred during rupture, then at
least locally temperatures were elevated, facilitating twinning. There is
no evidence that local conversion to hexagonal β-quartz was achieved
(650 °C at 1 GPa). The pseudotachylites studied here are of tectonic/
seismic origin but it should be mentioned that they also occur associated
with impacts (Reimold, 1995).
Quartz in brecciated fault rocks from the San Andreas Fault at
depth also shows twinning, and it is likely that also in this case it was
caused by seismic stresses. These are likely local stresses during an
earthquake, which is not inconsistent with the current creep mode of
the fault at Parkfield, with very low average stresses (Hickman and
Zoback, 2004; Townend and Zoback, 2004). SAFOD stresses based on
dislocation densities, twinning microstructures and preserved residual stresses in calcite were estimated at 100–200 MPa (Rybacki et al.,
2011), but some of these microstructures were attributed to creep.
Also in the SAFOD sample analyzed here, fragmention of quartz is
evidence of local stress exceeding the strength of quartz. What is the
strength of quartz?
The compressive strength of quartz is very high (1–5 GPa, Griggs
et al., 1960; Kimberley et al., 2010), but the tensile and shear strengths
are two orders of magnitude lower (30–50 MPa, Ball and Payne,
1976). Thus, in brecciated and fragmented quartz such stresses must
have been exceeded. This corresponds to stresses that can induce
Dauphiné twinning at low temperature and we should again keep in
mind that twins nucleate at local stress concentrations which are
likely much higher than average applied stresses. The experiment of
Schubnikov (1930) demonstrated that twinning occurs well below
fracture. The relative ease by which twinning occurs, raises the
possibility that some twins could be artifacts and have been produced
during sampling, e.g. extracting specimens with a geological hammer.
We do not think that this was the case for the specimens described
here. MEMIN and SAFOD samples were carefully cut with a microsaw.
And while pseudotachylite and mylonites were collected with a
hammer in the field, they were later also cut and internal portions
were used. So far bulk texture analyses of quartzites always show very
systematic orientation distributions that can be followed over large
distances (e.g. Pehl and Wenk, 2005). If sample extraction would alter
crystal orientations, this would not be the case. Nevertheless we
wanted to mention this possibility and should be aware of conceivable
artifacts.
Twinning has been documented in metamorphic rocks (e.g.
Heidelbach et al., 2000; Trimby et al., 1998) where it is, however,
not dominant. Particularly at higher metamorphic grade, pole figures
always display a strong difference between positive and negative
rhombs, which precludes pervasive twinning. This is also illustrated
for a greenschist-grade muscovite quartzite from the Bergell Alps in
Fig. 10. The microstructure consists of slightly flattened grains,
separated by muscovite flakes (Fig. 10a). Neutron diffraction pole
H.-R. Wenk et al. / Tectonophysics 510 (2011) 69–79
77
Fig. 9. SAFOD breccia 1B. Two regions of this sample are shown (a,c) and (b,d), both with fractured quartz clasts. (a,b) Photomicrographs taken with crossed polarizers. (c,d) EBSD
maps of Euler angle ϕ2, 1 μm steps. Dauphiné twin boundaries are red. Twinning is concentrated in the outer portions of the grains. White areas correspond to fine-grained matrix
that is largely feldspar.
figures measured on a 1 cm cube show a bimodal c-axis distribution
and a very distinct difference between positive and negative rhombs
(Fig. 10c, Wenk et al., 2010). Positive rhombs {1011} have a maximum
perpendicular to the schistosity plane s (horizontal). Below (Fig. 10d)
are EBSD pole figures measured on a small surface segment. Positive
rhombs show a clear maximum perpendicular to the schistosity plane.
This requires that there could not be equal fractions of twins and host
in each grain. The EBSD map (Fig. 10b) shows some twinning but
twins comprise only minor fractions, particularly at grain boundaries,
and at boundaries between quartz and muscovite. Some grains are
more profusely twinned than others, suggesting orientation control.
Indeed, in the EBSD pole figures (Fig. 10d) twin orientations can be
clearly identified (arrows). Statistically, over a large volume, this is
less evident (Fig. 10c).
The significance of these twins in metamorphic rocks is not clear:
are they growth twins forming during recrystallization under stress?
Is the difference between positive and negative rhombs due to slip or
twinning? If twinning has occurred at metamorphic conditions, why
has it not gone to completion? The morphology of twins in this
metamorphic quartzite is different from that in the stressed samples,
where a clear tendency exists for 120° angles of boundaries and twin
concentrations at grain corners. The role of twinning in metamorphic
rocks will be the subject of a future study.
Dauphiné twinning is not really a paleopiezometer because it does
not provide information about exact stress magnitudes (Tullis, 1980).
Initiation of twinning is highly orientation dependent (Schubnikov
and Zinserling, 1932). It also depends on temperature and, at
intermediate temperatures, nucleation of twins has been observed
at 50–100 MPa (e.g. Wenk et al., 2006, 2007). Nucleation of twins is
followed by propagation of twin boundaries and, in an equilibrium
situation, twinning should go to completion, which may be the reason
why quartz twin boundaries are rare in higher grade metamorphic
rocks. But high localized and transient stresses appear to impose
characteristic twin domain structures in quartz of impactites and
pseudotachylites, linking seismic events to meteorite impacts. This
investigation, mainly on natural rocks, cannot determine magnitudes
of local stresses to induce twinning and this should be approached
with modern methods such as nanoindentation (Wang et al., 2005) or
in situ electron microscopy (e.g. Ye et al., 2010). Similarly, deformation experiments, combined with EBSD analyses should be conducted
to determine the influence of crystal orientation relative to an applied
stress. With such additional data one may be able to better constrain
stress magnitudes.
5. Conclusions
The investigation documents abundant Dauphiné twinning in
quartz subjected to intense dynamic stresses (N100–200 MPa). In
natural rocks such conditions occur during meteorite impacts and
seismic rupture, with high local stress concentrations. This investigation has focused on a few grains in a few samples. Thus, our general
conclusions need to be corroborated in the future. For example, is
twinning common in brittle rocks, such as fault gouges? Is twinning
observed during spallation such as in deep mines? We would expect a
high twin density in quartz fragments ejected during impact. And a
systematic investigation of twinning should be conducted in metamorphic rocks. Interestingly, most texture studies of quartz still
emphasize pole figures of c-axes and a-axes, even though modern
78
H.-R. Wenk et al. / Tectonophysics 510 (2011) 69–79
Fig. 10. Metamorphic muscovite quartzite Brg 980 from the Bergell Alps. (a) Optical photomicrograph taken with crossed polarizers; schistosity plane is near horizontal. (b) EBSD
map of a small area with some Dauphine twins. White areas are muscovite. (c) Neutron diffraction analysis of a 1 cm cube illustrating a rather complex texture with large difference
between positive and negative rhombs. (d) EBSD pole figure of a small surface area from (b). Two orientations related by Dauphiné twinning are identified by arrows. Pole figures are
equal area projection, linear contours in multiples of a random distribution, s is the schistosity plane (horizontal).
diffraction techniques allow to distinguish between positive and
negative rhombs, and this trigonal orientation of quartz crystals
appears to be very relevant. Finally, twinning should depend on
crystal orientation. Are some orientations more twinned than others?
If this were established, it could become a method to determine the
direction of the highest stress.
Acknowledgements
This research was supported by grants from NSF (EAR-0836402),
DOE-BES (DE-FG02-05ER15637), DFG-MEMIN and DFG-SAFOD
(JA573/4-1). We are appreciative for samples obtained from the
Fraunhofer Institute in Efringen/Kirchen, the SAFOD team, from Prof.
U. Reimold (Berlin) and the Berlin Museum of Natural History. We
appreciate access to the HIPPO neutron diffraction facilities at LANSCE
and Sven Vogel for help with experiments. We are especially grateful
for reviews by Jan Tullis and an anonymous reviewer which helped us
to improve the presentation.
References
Baker, D.W., Wenk, H.-R., 1972. Preferred orientation in a low symmetry quartz
mylonite. J. Geol. 80, 81–105.
Ball, A., Payne, B.W., 1976. The tensile fracture of quartz crystals. J. Mat. Sci. 11, 731–740.
Barber, D.J., Wenk, H.-R., 1979. Deformation twinning in calcite, dolomite, and other
rhombohedral carbonates. Phys. Chem. Miner. 5, 141–165.
Barber, D.J., Wenk, H.-R., 1991. Dauphiné twinning in deformed quartzites: implications
of an in situ TEM study of the α–β phase transformation. Phys. Chem. Miner. 17,
492–502.
Bertagnolli, E., Kittinger, E., Tichy, J., 1979. Ferroelastic hysteresis in α-quartz. J. Appl.
Phys. 50, 6267–6271.
Bunge, H.-J., 1965. Zur Darstellung allgemeiner Texturen. Z. Metallk. 56, 872–874.
Chen, K., Kunz, M., Tamura, N., Wenk, H.-R., 2011. Evidence for high stress in quartz
from the impact site of Vredefort, South Africa. Eur. J. Miner. 23, 169–178.
Frondel, C., 1962. 7th edtn. The System of Mineralogy, Vol. 3. Wiley, New York.
H.-R. Wenk et al. / Tectonophysics 510 (2011) 69–79
Gibbs, R.E., 1926. Structure of α-quartz. Proc. R. Soc. 110A, 443–455.
Gibson, R.L., Armstrong, R.A., Reimold, W.U., 1997. The age and thermal evolution of the
Vredefort impact structure: a single-grain U–Pb zircon study. Geochimica and
Cosmochimica Acta 61, 1531–1540.
Goldschmidt, V., 1897. Krystallographische Winkeltabellen, Berlin.
Gratz, A.J., Tyburczy, J., Christie, J.M., Ahrens, T., Pongratz, P., 1988. Shock metamorphism of deformed quartz. Phys. Chem. Miner. 16, 221–233.
Gratz, A.J., Nellis, W.J., Christie, J.M., Brocious, W., Swegle, J., Cordier, P., 1992. Shock
metamorphism of quartz with initial temperatures − 170 to 1000 °C. Phys. Chem.
Miner. 19, 267–288.
Griggs, D.T., Turner, F.J., Heard, H.C., 1960. Chapter 4. Deformation of rocks at 500 to
800 C. In: Griggs, D., Handin, J. (Eds.), Rock Deformation: Geol. Soc. Am. Memoir,
vol. 79, pp. 39–104.
Hauy, R.J., 1801. Traité de Minéralogie, Chez Louis, Paris.
Heaney, P.J., Prewitt, C.T., Gibbs, G.V., 1994. Silica. Physical behavior, geochemistry and
materials applications. Reviews in Mineralogy. Min. Soc. Amer. 29, 606 pp.
Heidelbach, F., Kunze, K., Wenk, H.-R., 2000. Texture analysis of a recrystallized
quartzite using electron diffraction in the scanning electron microscope. J. Struct.
Geol. 22, 91–104.
Hickman, S., Zoback, M.D., 2004. Stress orientations and magnitudes in the SAFOD pilot
hole. Geophys. Res. Lett. 31 (15S12). doi:10.1029/2004GL020043.
Janssen, C., Wirth, R., Reinicke, A., Rybacki, E., Naumann, R., Wenk, H.-R., Dresen, G.,
2011. Nanoscale porosity in SAFOD core samples (San Andreas Fault). Earth Planet.
Sci. Lett. 301, 179–189.
Kenkmann, T., Wünnemann, K., Deutsch, A., Poelchau, M.H., Schäfer, F., Thoma, K., 2011.
Impact cratering in sandstone: the MEMIN pilot study on the effect of pore water.
Meteorit. Planet. Sci. 46, 890–902.
Kimberley, J., Ramesh, K.T., Barnouin, O.S., 2010. Visualization of the failure of quartz
under quasi-static and dynamic compression. J. Geophys. Res. 115, B08207.
doi:10.1029/2009JB007006 13 pp.
Klassen-Neklyudova, M.V., 1964. Mechanical Twinning of Crystals (translated from
Russian by JES Bradley). Consultants Bureau, New York. 213 pp.
Kunz, M., Chen, K., Tamura, N., Wenk, H.-R., 2009. Residual stress and domain
orientation in natural quartz. Am. Miner. 94, 1059–1062.
Lloyd, G.E., 2000. Grain boundary contrast effects during faulting of quartzite: an SEM/
EBSD analysis. J. Struct. Geol. 22, 1675–1693.
Lloyd, G.E., 2004. Microstructural evolution in a mylonitic quartz simple shear zone: the
significant roles of Dauphiné twinning and misorientation. In: Alsop, G.I., et al.
(Ed.), Transports and Flow Processes in Shear Zones. Geological Society of London,
Special Publication, 224, pp. 39–61.
Martini, J.E.J., 1978. Coesite and stishovite in the Vredefort Dome, South Africa. Nature
272, 715–717.
McSkimin, H.J., Andreatch Jr., P., Thurston, R.N., 1965. Elastic moduli of quartz versus
hydrostatic pressure at 25° and − 195.8 °C. J. Appl. Phys. 36, 1624–1632.
Partridge, P.G., 1967. The crystallography and deformation modes of hexagonal closepacked metals. Metall. Rev. 12, 169–194.
Pehl, J., Wenk, H.-R., 2005. Evidence for regional Dauphiné twinning in quartz from the
Santa Rosa mylonite zone in Southern California. A neutron diffraction study.
J. Struct. Geol. 27, 1741–1749.
Pfaff, F., 1859. Versuche über den Einfluß des Drucks auf die optischen Eigenschaften
doppeltbrechender Krystalle. Ann. Phys. 107, 333–338.
Reimold, W.U., 1995. Pseudotachylites in impact structures—generation by frictional
melting and shock brecciation? A review and discussion. Earth Sci. Rev. 39, 247–264.
Rybacki, E., Janssen, C., Wirth, R., Chen, K., Wenk, H.R., Dresen, G., 2011. Low-temperature
deformation of calcite veins of SAFOD core samples (San Andreas fault) –
microstructural analysis and implications for fault rheology. Tectonophysics 509,
107–119.
Schubnikov, A., 1930. Ueber Schlagfiguren des Quarzes. Z. Kristallogr. 74, 103–104.
Schubnikov, A., Zinserling, K., 1932. Ueber die Schlag- und Druckfiguren und ueber die
mechanischen Quarzzwillinge. Z. Kristallogr. 83, 243–264.
Seidel, G., 1992. Thüeringer Becken. Sammlung Geologischer Füehrer, 85. Bornträeger,
Berlin. 204 pp.
Sibson, R.H., 1975. Generation of pseudotachylite by ancient seismic faulting. Geophys.
J. R. astr. Soc. 43, 775–794.
79
Springer, D.S., Evans, J.P., Garver, J.L., Kirschner, D., Janecke, S., 2009. Arkosic rocks from
the San Andreas Fault observatory at depth (SAFOD) borehole, central California:
implications for structure and tectonics of the San Andreas Fault zone. Lithosphere
1, 206–226. doi:10.1130/L 13.1.
Stöffler, D., Langenhorst, F., 1994. Shock metamorphism of quartz in nature and
experiment. 1. Basic observation and theory. Meteoritics 29, 155–181.
Thomas, L.A., Wooster, W.A., 1951. Piezocrescence—the growth of Dauphiné twinning
in quartz under stress. Proc. R. Soc. London A 208, 43–62.
Townend, J., Zoback, M.D., 2004. Regional tectonic stress near the San Andreas fault in
central and southern California. Geophys. Res. Lett. 31, L15S11. doi:10.1029/
2003GL018918.
Trepmann, C.A., 2008. Shock effects in quartz: compression versus shear deformation—
an example from the Rochechouart impact structure, France. Earth Planet. Sci. Lett.
267, 322–332.
Trepmann, C.A., Spray, J.G., 2005. Planar microstructures and Dauphiné twins in
shocked quartz from the Charlevoix impact structure, Canada. Geol. Soc. Amer.
Special Paper, 384, pp. 315–328.
Trimby, P.W., Prior, D.J., Wheeler, J., 1998. Grain boundary hierarchy development in a
quartz mylonite. J. Struct. Geol. 20, 917–935.
Tullis, J., 1970. Quartz: preferred orientation in rocks produced by Dauphiné twinning.
Science 168, 1342–1344.
Tullis, T.E., 1980. The use of mechanical twinning in minerals as a measure of shear
stress magnitudes. J. Geophys. Res. 85, 6263–6268.
Tullis, J., Tullis, T.E., 1972. Preferred orientation produced by mechanical Dauphiné
twinning. Thermodynamics and axial experiments. Am. Geophys. U. Monogr. 16,
67–82.
Van Tendeloo, G., Van Landuyt, J., Amelickx, S., 1976. The α–β phase transition in quartz
and AlPO4 as studied by electron microscopy and diffraction. Phys. Stat. Solidi (a)
33, 723–735.
Vernooij, M.G.C., Langenhorst, F., 2005. Experimental reproduction of tectonic
deformation lamellae in quartz and comparison to shock-induced planar
deformation features. Meteorit. Planet. Sci. 40, 1353–1361.
Von Engelhardt, W., 1974. Ries meteorite crater, Germany. I. The Ries structure and its
impact formations. Fortschr. Mineral 52, 103–109.
Wang, Y.M., Hodge, A.M., Biener, J., Hamza, A.V., Barnes, D.E., Liu, K., Nieh, T.G., 2005.
Deformation twinning during nanoindentation of nanocrystalline Ta. Appl. Phys.
Lett. 86 (101915), 1–3.
Wenk, H.-R., 1998. Deformation of mylonites in Palm Canyon, California, based on
xenolith geometry. J. Struct. Geol. 20, 559–571.
Wenk, H.-R., Matthies, S., Donovan, J., Chateigner, D., 1998. BEARTEX, a Windows-based
program system for quantitative texture analysis. J. Appl. Cryst. 31, 262–269.
Wenk, H.-R., Johnson, L.R., Ratschbacher, L., 2000. Pseudotachylites in the eastern
Peninsular ranges of California. Tectonophysics 321, 253–277.
Wenk, H.-R., Lonardelli, I., Vogel, S.C., Tullis, J., 2005. Dauphiné twinning as evidence for
an impact origin of preferred orientation in quartzite: an example from Vredefort,
South Africa. Geology 33, 273–276.
Wenk, H.-R., Rybacki, E., Dresen, D., Lonardelli, I., Barton, N., Franz, H., Gonzales, G.,
2006. Dauphiné twinning and texture memory in polycrystalline quartz. Part 1:
experimental deformation of novaculite. Phys. Chem. Miner. 33, 667–676.
Wenk, H.-R., Bortolotti, M., Barton, N., Oliver, E., Brown, D., 2007. Dauphiné twinning
and texture memory in polycrystalline quartz. Part 2: in situ neutron diffraction
compression experiments. Phys. Chem. Miner. 34, 599–607.
Wenk, H.-R., Barton, N., Bortolotti, M., Vogel, S., Voltolini, M., Lloyd, G., Gonzalez, G.,
2009. Dauphiné twinning and texture memory in polycrystalline quartz. Part 3.
Texture memory during phase transformation. Phys. Chem. Miner. 37, 567–583.
Wenk, H.-R., Lutterotti, L., Vogel, S.C., 2010. Rietveld texture analysis from TOF neutron
diffraction data. Powder Diffract. 25, 283–296.
Wooster, W.A., Wooster, N., Rycroft, J.L., Thomas, L.A., 1947. The control and elimination
of electrical (Dauphiné) twinning in quartz. J. Inst. Electr. Eng. 94, 927–938.
Ye, J., Mishra, R.K., Sachdev, A.K., Minor, A.M., 2010. In situ TEM compression testing of
Mg and Mg–0.2 wt.% Ce single crystals. Scr. Mater. 64, 292–295.
Yoo, M.H., 1981. Slip, twinning and fracture in hexagonal close-packed metals. Metall.
Trans. 12A, 409–418.