* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Physics 231 Topic 8: Gravitation Wade Fisher October 24-26 2012
Survey
Document related concepts
Transcript
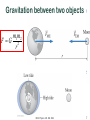
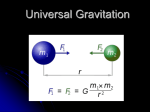
Physics 231 Topic 8: Gravitation Wade Fisher October 2012 MSU Physics24-26 231 Fall 2012 1 Clicker Quiz! 3 children are sitting on a rotating disc in a playground. The disc starts to spin faster and faster. Which of the three is most likely to start sliding first? top view A B C a) b) c) d) child A child B child C the same for all three ac= 2r A= B= c rA<rB<rc acA<acB<acC The centripetal force needed to stay in place is largest for C MSU Physics 231 Fall 2012 2 Key Concepts: Gravitation Newton’s Law of Gravitation Gravitational Acceleration Planetary Motion Kepler’s Laws Gravitational Potential Energy Conservation of ME Artificial Satellites Covers chapter 9 in Rex & Wolfson MSU Physics 231 Fall 2012 3 The gravitational force, revisited Newton: m1 m2 F G 2 r G=6.673·10-11 Nm2/kg2 The gravitational force works between every two massive particles in the universe, yet is the least well understood force known. MSU Physics 231 Fall 2012 4 Gravitation between two objects A B The gravitational force exerted by the spherical object A on B can be calculated by assuming that all of A’s mass would be concentrated in its center and likewise for object B. Conditions: B must be outside of A A and B must be ‘homogeneous’ MSU Physics 231 Fall 2012 5 Gravitation between two objects m1m2 F G 2 r The gravitational force exerted by the spherical object A on B can be calculated by assuming that all of A’s mass would be concentrated in its center and likewise for object B. The force of the earth on the moon is equal and opposite to the force of the moon on the earth! MSU Physics 231 Fall 2012 6 Gravitation between two objects m1m2 F G 2 r MSU Physics 231 Fall 2012 7 Gravitational acceleration m1mEARTH F G 2 F=mg r g=GmEARTH/r2 Radius from Earth’s Center (km) Gravitational Acceleration (m/s2) Earth’s Surface 6366 9.81 Mount Everest 6366 + 8.85 9.78 Mariana Trench 6366 - 11.03 9.85 Polar Orbit Satellite 6366 + 1600 6.27 Geosynchronous Satellite 6366 + 36000 0.22 MSU Physics 231 Fall 2012 8 Orbital Velocities What does the word orbit mean? An orbit is the gravitationally curved path of an object around a point in space. To orbit the object, you need to satisfy the kinematic conditions of that type of orbit (more on this shortly…) MSU Physics 231 Fall 2012 9 launch speed 4 km/s 6 km/s MSU Physics 231 Fall 2012 8 km/s 10 Gravitational potential energy So far, we used: PEgravity=mgh Only valid for h near earth’s surface. More general: PEgravity=-GMEarthm/r PE=0 at infinite distance from the center of the earth (r=∞) Earlier we noted that we could define the zero of PEgravity anywhere we wanted. So the surface of the earth is as good as anywhere! PE1 G R2 R1 mEARTH m R1 mEARTH PE2 G m R2 MSU Physics 231 Fall 2012 R1<R2 Thus… PE1 < PE2 11 Gravitational potential energy So far, we used: PEgravity=mgh Only valid for h near earth’s surface. More general: PEgravity=-GMEarthm/r PE=0 at infinite distance from the center of the earth (r=∞) Earlier we noted that we could define the zero of PEgravity anywhere we wanted. So the surface of the earth is as good as anywhere! R2=R1+h R2 R1 PE2 PE1 G mEARTH m m (G EARTH m) R2 R1 mEARTH mEARTH G m (G m) ( R1 h) R1 mEARTH 1 1 mGmEARTH ( ) m G 2 R1 R1 h R 1 MSU Physics 231 Fall 2012 h mgh 12 Gravitational potential energy So far, we used: PEgravity=mgh Only valid for h near earth’s surface. More general: PEgravity=-GMEarthm/r PE=0 at infinite distance from the center of the earth (r=∞) Example: escape speed (a.k.a. second cosmic speed ) what should the minimum initial velocity of a rocket be if we want to make sure it will not fall back to earth? KEi + PEi = ½mv2 - GMEarthm/Rearth KEf + PEf = 0 v = (2GMearth/REarth) = 11.2 km/s MSU Physics 231 Fall 2012 13 Some definitions First cosmic speed: speed of a satellite on a low-lying circular orbit (rsatellite ≈ rplanet): Msg = Msv2/r so v1 =(gr) where g = Gmplanet/rp2 For earth: g=9.81 m/s2 r=6.366x106 m v1=7.91x103 m/s Second cosmic speed: speed needed to break free from a planet: v1 =(2GMp/Rp) = (2gr) For earth: g=9.81 m/s2 r=6.366x106 m v2=1.12x104 m/s Synchronous orbit of a satellite: rotation period of satellite is the same as rotation period of the planet For earth: period T = 24 hours Angular speed = 2/(243600) = 7.27x10-5 rad/s For earth what is its radius? Use Fg=mac so Gmearthmsat/r2 = msat2r (note rrearth !) So r3=Gme/2 r=(Gme/2)1/3 = 3.54x107 = 35400 km MSU Physics 231 Fall 2012 14 launch speed = 10 km/s MSU Physics 231 Fall 2012 15 Clicker Quiz! Earth and Moon a) one quarter If the distance to the Moon were b) one half doubled, then the force of attraction c) the same between Earth and the Moon would be: d) two times e) four times The gravitational force depends inversely on the distance squared. So if you increase the distance by a factor of 2, the force will decrease by a factor of 4. Mm F G 2 R MSU Physics 231 Fall 2012 16 Kepler’s laws Johannes Kepler (1571-1630) MSU Physics 231 Fall 2012 17 Kepler’s First law Eccentricity: e c b e 1 a a 2 An object A bound to another object B by a force that goes with 1/r2 moves in an elliptical orbit around B, with B being in one of the focus point of the ellipse. MSU Physics 231 Fall 2012 18 Kepler’s First law p+q = constant An object A bound to another object B by a force that goes with 1/r2 moves in an elliptical orbit around B, with B being in one of the focus point of the ellipse. MSU Physics 231 Fall 2012 19 PEgravity=-GMEarthm/r Kepler’s second law Area(D-C-SUN)=Area(B-A-SUN) Potential energy is maximal, Kinetic energy is minimal Potential energy is close to 0 here, but still negative Potential energy is minimal, kinetic energy is maximal (potential energy is very negative here) A line drawn from the sun to the elliptical orbit of a planet sweeps out equal areas in equal time intervals. MSU Physics 231 Fall 2012 20 Kepler’s third law Consider a planet in circular motion around the sun: G M sun M planet r 2 M planet v 2planet r s 2r v t T 4 2 3 2 r K s r 3 T GM sun T2 Ks 3 r K s 2.97 10 19 s 2 / m 3 r3 C 2 T C 3.36 1018 m 3 / s 2 MSU Physics 231 Fall 2012 21 Kepler’s third law Consider a planet in circular motion around the sun: r3 r3 C 2 T C 3.36 1018 m3 / s 2 T2 r3=C T2 r3=constantT2 T: period-time it takes to make one revolution If the orbit is an ellipse, replace r with a, the semi-major axis. a=(half the sum of the smallest and greatest distance from the sun) MSU Physics 231 Fall 2012 22 An Example Two planets are orbiting a star. B The orbit of A has a radius of 108 km. The distance of closest approach of B to the star is 5x107 km and its maximum distance from the star is 109 km. If A has a rotational period of 1 year, what is the rotational period of B? star A Need to use Kepler’s 3rd Law, but Planet B orbits in an ellipse Recall: replace R with the average radius on the semi-major axis. R=½(a+b) MSU Physics 231 Fall 2012 23 An Example A Two planets are orbiting a star. The B orbit of A has a radius of 108 km. The star distance of closest approach of B to the star is 5x107 km and its maximum distance from the star is 109 km. If A has a rotational period of 1 year, what is the rotational period of B? Rmin = distance of closest approach. = perihelion Rmax = maximum distance = aphelion RA = 108 km RB = ½(rmin+rmax) = ½(5x107+109) = 5.25x108 km R3/T2 = constant RA3/TA2= RB3/TB2 so TB2=(RB3/RA3)TA2 So TB=(5.253 x (1 yr)2) = 12 years MSU Physics 231 Fall 2012 24 Clicker Quiz! Averting Disaster a) it’s in Earth’s gravitational field The Moon does b) the net force on it is zero not crash into c) it is beyond the main pull of Earth’s gravity Earth because: d) it’s being pulled by the Sun as well as by Earth e) its velocity is large enough to stay in orbit The Moon does not crash into Earth because of its high speed. If it stopped moving, it would fall directly into Earth. With its high speed, the Moon would fly off into space if it weren’t for gravity providing the centripetal force. MSU Physics 231 Fall 2012 25 For Next Week Chapter 10: Solids and Fluids Homework Set 8 Due Wednesday Nov 2! MSU Physics 231 Fall 2012 26