* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Ch. 2
Modified Newtonian dynamics wikipedia , lookup
Planets beyond Neptune wikipedia , lookup
Aquarius (constellation) wikipedia , lookup
Rare Earth hypothesis wikipedia , lookup
Chinese astronomy wikipedia , lookup
Astrobiology wikipedia , lookup
Patronage in astronomy wikipedia , lookup
Definition of planet wikipedia , lookup
Tropical year wikipedia , lookup
Archaeoastronomy wikipedia , lookup
IAU definition of planet wikipedia , lookup
International Year of Astronomy wikipedia , lookup
Philosophiæ Naturalis Principia Mathematica wikipedia , lookup
Astronomy in the medieval Islamic world wikipedia , lookup
Lunar theory wikipedia , lookup
History of Solar System formation and evolution hypotheses wikipedia , lookup
Satellite system (astronomy) wikipedia , lookup
Extraterrestrial life wikipedia , lookup
Formation and evolution of the Solar System wikipedia , lookup
Theoretical astronomy wikipedia , lookup
Astronomical unit wikipedia , lookup
Observational astronomy wikipedia , lookup
Copernican heliocentrism wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
Hebrew astronomy wikipedia , lookup
History of astronomy wikipedia , lookup
Geocentric model wikipedia , lookup
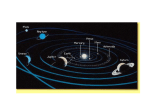
Lecture PowerPoint Chapter 2 Astronomy Today, 5th edition Chaisson Last revised: 2-Feb-10 McMillan © 2005 Pearson Prentice Hall This work is protected by United States copyright laws and is provided solely for the use of instructors in teaching their courses and assessing student learning. Dissemination or sale of any part of this work (including on the World Wide Web) will destroy the integrity of the work and is not permitted. The work and materials from it should never be made available to students except by instructors using the accompanying text in their classes. All recipients of this work are expected to abide by these restrictions and to honor the intended pedagogical purposes and the needs of other instructors who rely on these materials. Chapter 2 The Copernican Revolution Harlow Shapley Edwin Hubble Annie Jump Cannon Karl Jansky Units of Chapter 2 Ancient Astronomy (Archaeoastronomy) The Geocentric Universe – Aristotle & Ptolemy The Heliocentric Model of the Solar System The Foundations of the Copernican Revolution Copernicus and Galileo The Birth of Modern Astronomy Units of Chapter 2, cont. The Laws of Planetary Motion Kepler’sThree Laws Some Properties of Planetary Orbits The Dimensions of the Solar System Newton’s Laws – Laws of Motion & Gravity The Moon Is Falling! Weighing the Sun 2.1 Ancient Astronomy • Ancient civilizations observed the skies • Many built structures to mark astronomical events summer solstice Summer solstice sunrise at Stonehenge: There are hundreds of these type of constructs all over Europe sunrise over heelstone The Dawn of Astronomy Native American Astronomy in the SW US 2.1 Ancient Astronomy Spokes of the Big Horn Medicine Wheel (WY) are aligned with rising and setting of Sun and other stars 2.1 Ancient Astronomy Mayan Astronomy The Caracol temple at Chichen Itza has many windows that are aligned with astronomical events There are hundreds of various types of observatories all over the Americas 2.2 The Geocentric Universe Ancient and Medieval astronomers observed: Sun Moon Stars Five planets: Mercury, Venus, Mars, Jupiter, Saturn Muslim Astronomers Middle Ages For more information on the contributions of different world cultures to astronomy see the “History of Astronomy” Study Guide For more details on ancient observatories and astronomers go to the same Study Guide Ancient Western World (Greek Philosopher-Scientists) Plato Aristotle Thales Anaximander Aristarchus Hipparchus Claudius Ptolemy Eratosthenes Hypatia Early Greek Astronomy Greek Astronomy Timeline 2.2 The Geocentric Universe Early observations: • Inferior planets never too far from Sun • Superior planets not tied to Sun; exhibit retrograde motion • Superior planets brightest at opposition • Inferior planets brightest near inferior conjunction 2.2 The Geocentric Universe Sun, Moon, and stars all have simple movements in the sky Planets: • move with respect to fixed stars • change in brightness • change speed • have retrograde motion 2.2 The Geocentric Universe Earliest models had Earth at center of solar system Needed many computations to accurately track planetary motions: This is the Ptolemaic Cosmos using the Epicycle model of Hipparchus to account for retrograde motions Epicycle Model for Retrograde Motion Hipparchus How epicycles make retrograde loops The Ptolemaic Cosmos Refinement of Epicycle Model Geocentric vs. Heliocentric Cosmos • Still used circles & uniform circular motion 2.2 The Heliocentric Universe • Inferior planets: Mercury, Venus • Superior planets: Mars, Jupiter, Saturn Now know: Inferior planets have orbits closer to Sun than Earth’s Superior planets’ orbits are farther away Solar System Nomenclature 2.3 The Heliocentric Model of the Solar System The Sun is at center of solar system Only Moon orbits around Earth; planets orbit around Sun Here retrograde motion explained as a projection effect Retrograde Motion in the Heliocentric Cosmos A Projection Effect Stellar Background Earth moves faster outer planet moves slower retrograde loop Planet only appears to make a loop Ancients really thought it was 2.4 The Birth of Modern Astronomy Telescope invented around 1600 (NOT by Galileo but Hans Lippershay) Galileo built his own, made the following observations: • Moon has mountains and valleys • Sun has sunspots, and rotates • Venus has phases • Jupiter has 4 moons Galileo’s drawing Astronomy as Physics (The Beginning of the Scientific Revolution) 2.4 The Birth of Modern Astronomy Phases of Venus, in particular, cannot be explained by the geocentric model Phases of Venus crescent gibbous Note change in the angular size with Venus’s distance from Earth Near inferior conjunction Near superior conjunction The Waning of Aristotle 2.5 The Laws of Planetary Motion Kepler’s laws were derived by using the pre-telescopic observations made by Tycho Brahe Brahe Brahe’s Giant Quadrant at Uraniborg Observatory on the Isle of Hveen 2.5 Kepler’s Laws of Planetary Motion 1. Planetary orbits are ellipses, Sun at one focus 2.5 Kepler’s Laws of Planetary Motion 2. Imaginary line connecting Sun and planet sweeps out equal areas in equal times The Law of Equal Areas Aphelion perihelion Kepler’s Second Law 2.5 Kepler’s Laws of Planetary Motion 3. Square of period of a planet’s orbital motion is proportional to the cube of the semimajor axis P2 = ka3 P2 = ka3 Note: these are log scales Orbital Speed vs. Distance Comparing the Models: Copernican vs. Kepler 2.6 The Dimensions of the Solar System Astronomical unit (AU): mean distance from Earth to Sun (93 x 106 mi =150 x 106 km) First measured during transits of Mercury and Venus, using triangulation Now done using radar 2.6 The Dimensions of the Solar System Now measured using radar (Arecibo Obs.): Ratio of mean radius of Venus’s orbit to that of Earth very well known 2.7 Newton’s Laws •Newton’s laws of motion explain how objects interact with the world and with each other. •Newton published his work in the famous Principia Mathematica in 1687 Isaac Newton •Sir Edmund Halley was the driving force to get Newton to publish his work to the world •Halley used it to predict the return of the comet that now bears his name Edmund Halley 2.7 Newton’s Laws Newton’s First Law (The Principle of Inertia): An object at rest will remain at rest, and an object moving in a straight line at constant speed will not change its motion, unless an external force acts on it. at rest constant speed external force 2.7 Newton’s Laws Newton’s second law (F = ma) When a force is exerted on an object, its acceleration is inversely proportional to its mass: a = F/m Newton’s third law (Action = Reaction) When object A exerts a force on object B, object B exerts an equal and opposite force on object A. Illustrations of Newton’s 3 Laws of Motion Inertia F = ma Axn = Rxn 2.7 Newton’s Laws Gravity On the Earth’s surface, acceleration is approximately constant (g), and directed toward center of Earth: g = GME RE2 Wt. = mg 2.7 Newton’s Laws Gravity For two massive objects, gravitational force is proportional to the product of their masses divided by the square of the distance between them: Electricity, magnetism and intensity of light also follow inverse square laws 2.7 Newton’s Laws Gravity The constant G is called the Universal Gravitational Constant; it is measured experimentally and found to be: G = 6.67 × 10–11 N m2/kg2 2.7 Newton’s Laws Kepler’s laws are a consequence of Newton’s laws Possible Orbital Paths in Newton’s Theory of Gravity 2.7 Newton’s Laws Circular velocity: minimum speed needed to go into a circular orbit Escape velocity: speed necessary for a projectile to completely escape a planet’s gravitational field “Newton’s Cannon” orbits elliptical parabolic orbits hyperbolic How fast to orbit or escape Earth? units: vcirc = 7900 m/s = 7.90 km/s = 4.9 mi/s = 17,700 mi/hr Anything that can fly this fast will not hit the ground. This is the speed for low Earth orbital objects like the Space Shuttle, the ISS (International Space Station) and spy satellites. How fast to orbit the Moon or to escape from it? Newton’s Contributions Summary of Chapter 2 • First models of solar system were geocentric, but couldn't easily explain retrograde motion • Heliocentric model does; also explains brightness variations • Galileo's observations supported heliocentric model • Kepler found three empirical laws of planetary motion from observations Summary of Chapter 2, cont. • Laws of Newtonian mechanics explained Kepler’s observations • Gravitational force between two masses is proportional to the product of the masses, divided by the square of the distance between them