Download Lecture 05.2b

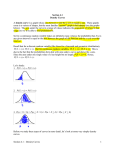
Econ 201
May 7, 2009
Indifference Curves
Budget Lines
and
Demand Curves
1
Where Are We Going?
• Indifference (iso-utility) curves can be
used with budget lines to provide a more
rigorous derivation of consumer demand
behavior
• Provide a richer insight into consumer
behavior than simple demand curves
• Used to provide a mathematical
foundation for analysis/modeling
2
What Are Indifference Curves
• An indifference curve in microeconomic theory
is a graph showing different bundles of goods,
each measured as to quantity, between which a
consumer is indifferent. That is, at each point on
the curve, the consumer has no preference for
one bundle over another.
• One can equivalently refer to each point on the
indifference curve as rendering the same level of
utility (satisfaction) for the consumer.
3
What Do They Look Like?
4
Perfect Substitutes
• Goods X and Y are perfect substitutes. The gray line perpendicular
to all curves indicates the curves are mutually parallel.
5
Perfect Complements
•
Three indifference curves where Goods X and Y are perfect substitutes. The
gray line perpendicular to all curves indicates the curves are mutually parallel.
6
Properties of Indifference Curves
•
•
•
•
•
•
Indifference curves are typically represented to be:
1. defined only in the positive (+, +) quadrant of commodity-bundle quantities.
2. negatively sloped. That is, as quantity consumed of one good (X) increases, total
satisfaction would increase if not offset by a decrease in the quantity consumed of the
other good (Y). Equivalently, satiation, such that more of either good (or both) is
equally preferred to no increase, is excluded. (If utility U = f(x, y), U, in the third
dimension, does not have a local maximum for any x and y values.)
3. complete, such that all points on an indifference curve are ranked equally preferred
and ranked either more or less preferred than every other point not on the curve. So,
with (2), no two curves can intersect (otherwise non-satiation would be violated).
4. transitive with respect to points on distinct indifference curves. That is, if each point
on I2 is (strictly) preferred to each point on I1, and each point on I3 is preferred to
each point on I2, each point on I3 is preferred to each point on I1. A negative slope
and transitivity exclude indifference curves crossing, since straight lines from the
origin on both sides of where they crossed would give opposite and intransitive
preference rankings.
5. (strictly) convex (sagging from below). With (2), convex preferences implies a
bulge toward the origin of the indifference curve. As a consumer decreases
consumption of one good in successive units, successively larger doses of the other
good are required to keep satisfaction unchanged, the substitution effect.
7
Simpler Version of the Properties
• Indifference curves are negatively sloped
– Graphically illustrates the trade off (in quantities)
required between the amounts of two goods while
maintaining the same “utility” (or level of satisfaction)
– Tradeoff  Marginal Rate of Substitution
• Indifference curves are convex to the origin
– Diminishing marginal utility
• As you greater/larger amounts of 1 good (e.g., X), it takes
increasingly greater amounts of Y to keep on the same U
curve
• Indifference curves don’t cross (would violate
rationality)
8
Key Assumptions
• Rationality (called an ordering relationship in a
more general mathematical context):
Completeness + transitivity. For given
preference rankings, the consumer can choose
the best bundle(s) consistently among a, b, and
c from lowest on up.
• Continuity: This means that you can choose to
consume any amount of the good. For example,
I could drink 11 mL of soda, or 12 mL, or 132
mL. I am not confined to drinking 2 liters or
nothing. See also continuous function in
mathematics.
9
Why Do They Have That Shape?
• Implications of transitivity and rationality
– U(I3) > U(I2) > U(I1)
– Concavity gives curves their shape
10
Budget Line/Constraint
Two goods
Consider a world of two goods, called
and
, which can be purchased in quantities
denominated by and , respectively. Let the price of
be
and the price of
be
. Finally, let the income of the consumer be denoted by
.
When the consumer purchases quantities
and
, his total spending is
The budget constraint states that total spending cannot exceed his revenue:
The graphical representation of the budget constraint is the budget line which represents
the maximum quantity of
the consumer can purchase for any given quantity of
The maximum quantity of
maximum quantity of
that can be purchased (i.e., if
that can be purchased (i.e., if
) is
) is
. The
.
When the consumer spends all his income we have
11
Graphical Version of the Budget
Constraint
12
Utility Maximization
• Assume consumer is going to Max U, subject to a budget contraint
– Get out to the highest U curve in the opportunity set (or budget)
– Which is point C given this budget constraint (blue)
13
Deriving the Demand Curve
• Decreasing the price of good Y; while
keeping the price of good X constant
– BC remains at same pt on x-axis (I/p(x))
– BC shifts out on the x-axis; as price
decreases you can buy more Y
• Max(Y) = I/p(Y)
• P1 > P2 > P3 => Y1 < Y2 < Y3
– Yields greater utility
14
Deriving the Demand Curve
•
A higher price of A means that less of A can be purchased
– budget line moves to the left, intersecting the vertical axis at a lower point.
– Point c is no longer possible and the consumer must move to a new position,
.
which, assuming utility maximization, will be point b
15
Deriving the Demand Curve
More than 1 price change
(3)
16
Ordinal vs. Cardinal Utility
Ordinal Utility
Interpersonal comparisons in utility can
not be made as scales differ for different
individuals
Cardinal
Would imply interpersonal comparisons
could be made as scales are absolute,
e.g., Centrigade/Farenheit
17